LE VERRIER ou le Triomphe du Calcul

(2011, l'Odyssée de Neptune, #2 )

Coup d'Essai, Coup de Maître

Ce que le Mathouriste et les mathématiciens admirent le plus chez Le Verrier, ce n'est pas son succès le plus médiatique (Neptune), mais... sontout premier papier en astronomie, sur la stabilité du système solaire. Car c'est là que, pour la première fois, un mathématicien détermine ce qu'on appelle les valeurs propres d'une matrice. Ce calcul est , après la résolution des systèmes linéaires, un de ceux qui absorbent aujjourd'hui la part la plus importante du temps de calcul des ordinateurs.

	ci-contre: L'article de Le Verrier, dans le Journal de Liouville, ou JMPA (tome 5, 1840)
	"Le premier Mémoire astronomique de Le Verrier fut présenté à l'Académie des Sciences le 16 septembre 1839; il a pour titre Sur les Variations Séculaires des Orbites des Planètes. Dans ce travail, l'auteur aborde l'une des questions les plus importantes de l'Astronomie: la stabilité du système planétaire. Si les planètes n'obéissaient qu'à l'action du Soleil, elles décriraient autour de lui des ellipses, conformémment aux lois de Képler; mais elles agissent les unes sur les autres, elles agissent également sur le Soleil, et de ces attractions diverses il résulte, dans leur mouvement elliptique, des perturbations que Képler navait pu prévoir avec les observations peu précises de Tycho Brahé [...]. La solution rigoureuse de ce problème surpasse de beaucoup les ressources actuelles de l'Analyse, et l'on est forcé de recourir à des approximations.[...] Des géomètres français éminents, Laplace, Lagrange, Poisson, avaient montré [que] les distances moyennes des planètes au Soleil restent toujours invariables. Plusieurs questions intéressantes se présentaient ensuite. Les orbites des planètes ont-elles toujours été et resteront elles toujours à peu près circulaires? Leurs inclinaisons mutuelles seront-elles toujours comprises dans des limites assez resserrées? Ces questions avaient été résolues par Laplace, qui avait conclu à la stabilité indéfinie du système planétaire. Mais la démonstration de Laplace n'était pas concluante, surtout pour les planètes dont les masses sont petites; un calcul numérique long et pénible pouvait seul décider si notre système planétaire ne peut éprouver que de petites oscillations périodiques autour d'un certain état moyen.
Le Verrier entreprit ce calcul, dans lequel, entre bien d'autres difficultés, il eut à résoudre une équation du septième degré fort compliquée [...]. Citons entre autres ce résultat important auquel il est arrivé: pendant vint-quatre mille ans, l'orbite de la Terre ira en se rapprochant sans cesse de la forme circulaire, sans l'atteindre cependant; après quoi elle sen éloignera pendant un temps très long, pour s'en rapprocher ensuite, etc. .." F.-F. Tisserand, Les Travaux de Le Verrier (1880)

Nous avons mis en relief le mot perturbations : nous y reviendrons avec des explications illustrées un peu plus loin, car il sera aussi au cœur de la découverte de Neptune. Mais revenons à nos mathématiques, en ne retenant de l'astronomie que l'obligation d'étudier 7 planètes à la fois, comme F.-F. Tisserand -un de ses successeurs à l'observatoire- l'a rappelé ci-dessus.

Vous trouverez, sur le site BibNum, un commentaire suivi de l'article, par l'auteur de cette page: il vous permettra de comprendre la démarche de Le Verrier avec des exemples plus simples, et de suivre son véritable calcul numérique, qui ne figure pas dans l'article ci-dessus. Le seul prérequis est la connaissance des opérations matricielles sur des exemples de petite taille; et si c'est encore trop... voici une présentation encore plus simplifiée.

Une petie idée

Supposons d'abord qu'il n'y ait que deux planètes, par exemple les deux plus grosses: Jupiter et Saturne. Vous vous dites sûrement que le problème est plus simple... mais non, car avec le Soleil, cela fait trois corps, et personne ne sait déterminer exactement les trajectoires! Autrement dit, ce que disait Tisserand en 1880 est encore vrai aujourd'hui, et même "plus que jamais": en étudiant de façon approfondie le problème des trois corps (1889), Poincaré a révélé son effrayante complexité, pire que tout ce que pouvaient imaginer les astronomes jusque'alors -l'acte de naissance de la théorie du Chaos.

Ce qui est plus facile à regarder, en revanche, c'est le système issu de l'approximation utilisée par Le Verrier dans sa résolution: il aura 2 inconnues (une par planète) et 2 équations au lieu de 7. Il a le même modèle que celui de deux oscillateurs couplés sans amortissement. Un tel système est de la forme suivante: deux inconnues de position (une pour chaque objet), et l'application de la relation fondamentale de la dynamique qui relie les positions aux accélérations -leurs dérivées secondes. Le couplage apparait dans le fait que l'équation en x contient y, et inversement.

γ_x = a x + b y	soit	x"(t) = a x (t) + b y (t)
γ_y = c x + d y	soit	y"(t) = c x (t) + d y (t)

Ce serait beaucoup plus sympathique, pour ne pas dire un jeu d'enfant, si les équations étaient découplées en deux braves et inoffensives équations à coefficients constants

X"(t) =	g₁ X (t)
Y"(t) =	g₂ Y (t)

C'est là que le problème d'analyse (résolution d'équations différentielles) bascule en un problème d'algèbre, teinté de géométrie.

Encadré technique 1 : Valeurs propres... pour les Nuls!

Oublions un instant les dépendances en fonction du temps. On peut voir (x, y) d'une part, (X, Y) d'autre part, comme deux systèmes de coordonnées d'un même point du plan, dans deux bases différentes.
La seconde aurait peut être des vecteurs un peu moins "beaux", mais aurait l'avantage décisif de rendre bien plus simple à réaliser graphiquement la transformation du point M (x, y) en le point M₁ (x₁ = a x + b y , y₁ = c x + d y).
Cela deviendrait tout simplement: transformation du point M (X, Y) en le point M₁ (X₁ = g₁ X , Y₁ = g₂ Y).
Et la construction serait bien plus immédiate: projeter sur les deux axes, et dilater chacune des coordonnées.

Le problème est donc le suivant: étant donnés a, b, c, d , définissant la transformation u, rechercher
1) les g tels que l'on peut trouver un vecteur V pour qui u (V) = g V ; (valeurs propres)
2) les vecteurs V associés, en tâchant d'en constituer une base. (vecteurs propres)
Le mot propre se réfère a la transformation: on recherche des directions privilégiées pour elles (elles ne varient pas, leurs vecteurs sont simplement dilatés), bref, qui lui appartiennent en propre.


s

On explicite, pour 1), le système sous la forme u (V) - g V = 0
Le système étant présenté matriciellement en ( A - g I ) V = 0, où I est la matrice identité, on écrirait aujourdhui l'existence d'une solution non triviale par

P (g) = det ( A - g I ) = 0

Mais... que fait Le Verrier?

Il écrit le système explicitement

(a - g) x + b y = 0 (1)

c x + (d - g) y = 0 (2)

Puis il combine les équations pour éliminer y de la première, x de la seconde

[ (a - g) (d - g) - bc ]x = 0	par	(d - g).(1) - b.(2)
[ (a - g) (d - g) - bc ] y = 0	par	(a - g).(2) - c.(1)

Il ne peut y avoir de solutions non triviales que si

(a - g) (d - g) - bc = g² - (a + d ) g + (a d - bc) = 0

Et voilà! Le polynôme caractéristique est apparu... de façon un peu plus rustique qu'à la manière moderne.

. Une suggestion pour aborder "en douceur" lalgèbre linéaire en général, et les valeurs propres en particulier:
G. STRANG, Linear Algebra and its Applications (Academic Press)

Oui, mais...
dans tout cela, n'oublions pas que Le Verrier, lui, traite avec un système 7 x 7 et non 2 x 2. La différence , cest qu'alors qu'il voit fort bien la forme de son équation caractéristique: un polynôme en g de degré 7, qu'il est capable d'en calculer aussi le terme de degré 6, qui est tout simplement la somme des coefficients diagoanux -ce que l'on appelle de nos jours trace de la matrice- il ne peut pour autant le calculer entièrement: tout étudianr averti du calcul des déterminants sait qu'il y aurait 7! = 5040 termes à réduire en les groupant par degré; évidemment, c'est surhumain! Pour ceux qui en douteraient, rappelons que cela vait fait reculer Laplace...


L'article "jumeau", publié à la	les valeurs numérique y sont explicitée; ce n'est pas le cas dans celui du JMPA.
Connaissance des Temps pour l'An 1843

Il commence par exploiter habilement le contexte du problème: si les trois grosses planètes (Jupiter, Saturne, Uranus) agissent de façon sensible sur les quatre petites (Mercure, Vénus, Terre, Mars), la contribution inverse est tout à fait négligeable. Ce qui lui permet de scinder le système 7 x7 en un système 3 x 3 (comme si on supprimait les petites planètes pour étudier seulement le système des trois grosses) puis un système 4 x 4. Les valeurs effectives des coefficients données dans larticle confirment cette idée: ils sont suffisemment petits pour les remplacer par des zéros sans altérer fiortement els résultats. La matrice 4 x 4 restante n'a cependant rien d'un gentil exercice de mathématiques où les coeffiicients sont des entiers entre -10 et +10, qu'on en juge!

La matrice 4 x 4 restant à traiter (coin haut & gauche du système précédent)

Le calcul du polynôme caractéristique n'est encore guère affriolant; mais Le Verrier va trouver une nouvelle astuce. Elle repose sur la simplicité de l'expression du terme de degré immédiatement inférieur, ou trace: c'est la somme des coefficients diagonaux. Ainsi, avec la matrice 4 x 4 ci-dessus, Le Verrier sait que

P (g) = g⁴ – 47.8884301 g³ + ???

Pour la simplicité, nous expliquons une nouvelle fois l'analogue dans le cas 2 x 2

Encadré technique 2 : Fonctions Symétriques et Traces

À l'époque où l'on faisait un tant soit peu de mathématiques en seconde (Je vous parle d'un temps que les moins de vingt ans ne peuvent pas connaître...), on y apprenait -et malheur à qui l'oubliait! - que les coefficients du polynôme du second degré "normalisé" (coefficient de plus haut degré : 1) étaient la somme et le produit des racines, comme le montre un développement élémentaire.

P (g) = (g - α) (g - β) = g² - (α + β ) g + αβ

Cela se généralise à n'importe quel degré: les coefficients sont les fonctions symétriques élémentaires des racines. Mais il y a d'autre fonctions symétriques qui constituent un jeu équivalent, en ce sens que, si l'on connait l'un, on connait aussi bien l'autre; c'est le cas des sommes de puissances, ou sommes de Newton. Au degré 2,

S₁ = α + β ; S₂ = α² + β²

Mais comme, pour le polynôme caractéristique, les carrés des racines seront les valeurs propres... de la matrice A², on accèdera à S₂ par un simple calcul de trace pour A².

Mais... que fait Le Verrier?

Son système étant 4 x 4, il devra calculer les traces de

A , A², A³, A⁴.

Mais... le calcul matriciel n'étant pas encore inventé (!), il le fait de manière déguisée, par des dérivations et substitutions dans son système différentiel. Le nouveau système fait intervenir g² au lieu de g, c'est donc le calcul de la trace de A² qui est en marche...

Et voilà le résultat! (Il a préalablement fait de même pour le système 3 x 3, un peu plus aisé à manier. )

Comme vous pourrez le lire dans notre commentaire suivi de l'article , l'algèbre linéaire donne beaucoup plus de confort ) l'application de la méthode. Elle a d'ailleurs été perfectionnée dans sa disposition par un autre Français, Jean-Marie Souriau (1948), et, indépendamment, par le Russe Dimitri Fadeev (1949) : on parle alors d'algorithme de Souriau-Fadeeev (et en allemand, avec un exemple développé) On peut aussi lire en ligne l'article original de Souriau.

Certes, cette méthode n'a plus aujourd'hui qu'un intérêt historique (on a depuis écrit une abondance d'épais livres sur les méthodes numériques matricielles), mais cet article demeure un jalon remarquable des mathématiques, car:

C'est la première fois... le polynôme caractéristique d'une matrice apparait! Alors que l'algèbre linéaire n'en est qu'à ses balbutiements;
C'est la première fois quon donne une méthode numérique de calcul des valeurs propres (beaucoup suivront,
C'est le passage des modes propres de l'Analyse de Fourier à celui des valeurs propres en Algèbre. Au contraire de tous les usages éducatifs, avec Fourier l'étude avait commencé en dimension infinie, et voici qu'on la retrouve en dimension finie (mais toujours au service d'équations différentielles)!

De Fourier à Le Verrier,

un petit tronçon d'une longue route...

"Propre (1090, du latin propius) :1° Qui appartient d'une manière exclusive ou particulière à une personne ou à une chose"

Dictionnaire Robert

Oui, c'est le tout premier sens du mot en Français, il est peut-être bon de le rappeler!

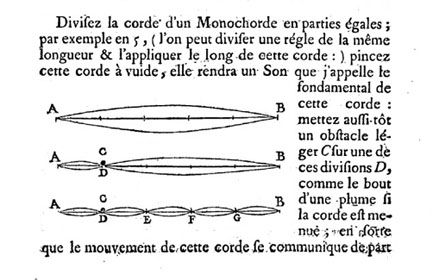
Les premiers "trucs propres" (si l'on ose dire) à apparaître en mathématiques/physique sont les modes propres de vibration d'une corde. Quoi de plus naturel, de plus familier? Joseph Sauveur (1653-1716), mathématicien de son état, considéré comme fondateur de l'acoustique, remarque qu'une corde fixée à ses deux extrémités ne peut vibrer que de certaines façons bien particulières, propres à la corde, donc, émettant ce qu'il appelle lui même harmoniques de sa note jouée "à vide"... puis Brook Taylor,leur donne leur forme mathématique sinusoïdale.

Le précurseur de Fourier, Daniel Bernoulli, a l'audace de penser que toute vibration complexe peut se décomposer en somme de vibrations propres, déclenchant ainsi une belle polémique scientifique avec Euler et d'Alembert. Fourier développe la même idée, avec une plus grande généralité, dans l'étude de la diffusion de la chaleur, dont les solutions sont décrites comme une somme (infinie) de modes élémentaires, ou propres.

Avec Le Verrier, c'est un vecteur de solutions ( décrivant le mouvement d'un système mécanique) qui est décomposé en combinaison finie de solutions vectorielles propres. C'est en tout cas ce que nous voyons aujourd'hui, bien avertis de l'algèbre linéaire dont ne disposait pas encore le héros de l'histoire....
Dans un cas comme dans l'autre, une équation "délicate" (équation aux dérivées partielles pour Fourier, système différentiel pour Le Verrier) a été atomisée en plusieurs équations très simples, du type y" + k² y = 0. Décomposer, recomposer...

L'histoire est ainsi allé à contresens de la progression pédagogique courante, en commençant par la dimension infinie. Mais de manière surprenante, Fourier avait eu, en physicien, l'intuition qualitative des modes propres pour un système mécanique fini... et dans un travail de jeunesse! Est-il possible que cela ait, au moins partiellement, guidé son intuition mathématique pour la chaleur?

" On peut encore démontrer [...] une proposition importante que Daniel Bernoulli a connu le premier et prouvée dans plusieurs cas particuliers: c'est que les petites oscillations des corps se composent d'escillations simples qui s'accomplissent en même temps sans se nuire. [...]

On sait que les équations qui représentent les mouvements du système sont du second ordre et linéaires: ces équations sont entre les indéterminées arbitraires dont dépendent toutes les coordonnées. En substituant de nouvelles indéterminées aux précédentes, on peut, généralement parlant, obtenir des équations séparées de la forme

q"(t) + K q(t) = 0

il est facile de s'en assurer [...]. On en conclura que, si l'on fixe sur un axe commun horizontal différents pendules simples, leurs mouvements peuvent correspondre parfaitement avec ceux du système. [...] Les coordonnées des divers points sont des fonctions linéaires des arcs décrits par les pendules [...]. Ces pendules étant d'abord placés de manière à représenter l'état initial du système, puis abandonnés à l'action de la pesanteur, jointe à la vitesse initiale, détermineront à chaque instant la position actuelle du système; et tous les mouvements dont le même corps est susceptible seront pareillement représentés par ceux du même assemblage de pendules.

J. Fourier, Mémoire sur la Statique in Journal de l'École Polytechnique, cahier n°5,2 (1798)
republié dans les Œuvres complètes, tome 2

Le cadre de Fourier était l'étude de la statique, mais cela l'a conduit à envisager la stabilité autour de l'équilibre: c'est exactement le sujet que doit affronter Le Verrier! Et Fourier nous annonce que la solution est toujours une combinaison de modes propres, chacun représenté physiquement par un pendule simple. On ne lui en voudra pas de la "petite" erreur qui consiste à ne voir que le cas diagonalisable; on sait très bien qu'il se rencontre avec la probabilité 1 dans les problèmes réels.

L'histoire se poursuivra à nouveau en dimension infinie avec des décompositions en modes propres de plus en plus variés (théorie de Sturm-Liouville, 1836), puis au tournant du XXème siècle avec la théorie des opérateurs linéaires (Banach, Hilbert) et la recherche des états quantiques de l'atome (Schrödinger, 1926).

La Traque de Neptune

" Je pense qu'un moment viendra où la solution du mystère d'Uranus sera peut-être fournie par une nouvelle planète, dont les éléments seraient reconnus par son action sur Uranus et vérifiés par celle qu'elle exerce sur Saturne."

F. Bessel, Lettre à Alexander von Humboldt (1845)

Les Caprices d'Uranus


Buste de William Herschel	Ses instruments d'observation	Herschel et Caroline, dans leur jardin
The William Herschel Museum, Bath (Angleterrre)

" Le décret de la Convention, qui, en 1795, avait créé le Bureau des Longitudes, chargeait expressément cet organisme de perfectionner les tables astronomiques. Sous la haute direction de Laplace, la besogne fut répartie entre les astronomes éprouvés: Delambre, Alexis Bouvard, Burckahrdt.
C'est à Bouvard qu'étaient échues les tables des 3 grosses planètes alors connues, Jupiter, Saturne et Uranus. Il s'attaqua à la dernière en 1821; il rencontra alors des difficultés inattendues, qui lui parurent insurmontables.
Uranus avait été découvert fortuitement par Herschel 40 ans plus tôt, en 1781. Cette planète, dont la période est de 84 ans, n'avait donc pas accompli, depuis sa découverte, la moitié de sa révolution, mais elle avait été observée une vingtaine de fois entre 1690 et 1781, ce qui étendait à 131 ans la période couverte par les observations. [...]

Bouvard calcula les perturbations d'Uranus par les autres planètes, l'action de Saturne étant la plus considérable, et il en corrigea les positions observées, mais sans parvenir à déterminer une ellipse képlerienne. Les observations, dépouillées de l'effet des perturbations, auraient dû obéir aux lois de Képler, mais en fait, elles s'en écartaient.

[...] Bouvard espérait sans doute que de nouvelles observations d'Uranus confirmeraient la correction de ses tables et qu'ainsi, toutes les difficultés qu'il avait rencontrées s'évanouiraient. Vaine illusion! Dès 1830, le désaccord était de nouveau flagrant, inadmissible. Ainsi, le sacrifice des observations anciennes n'avait pas assuré une représentation satisfaisante des observations les plus récentes et les plus précises, et le mouvement d'Uranus jetait indiscutablement un défi à la mécanique céleste. "

A.Denjon, Le Centenaire de la Découverte de Neptune (1946)

C'est que la magnifique simplicité de la loi d'attraction de Newton cache... une redoutable complexité. Si, en première vision, elle assigne à chaque planète une orbite elliptique autour du soleil qui l'attire, elle est tellement universelle... qu'une planète ressent parfois, de façon non négligeable, l' effet d'attraction de ses consœurs. Ce que les astronomes ont appelé perturbation, parce que cela perturbe le beau mouvement elliptique de Képler, considéré -avec raison- comme le mouvement principal, et à partir duquel on évalue la modification.

Les Perturbations

Commençons par un petit détour technique (qualitativement, sans aucun calcul !) pour bien comprendre de quoi il s'agit, de quoi est faite sur ce point la "routine" des astronomes, et en quoi ce que Le Verrier va avoir à faire est autrement difficile. Histoire de ne pas être... perturbé!

"Toutefois, dans le cas du système solaire, des circonstances heureuses rendent la solution du problème accessible [...]
Grâce à sa masse, qui vaut environ 700 fois celle de toutes les planètes réunies, le Soleil occupe une place prépondérante et mérite vraiment son nom d'astre central. Les grosses planètes, Jupiter et Saturne, viennent bien loin en arrière, leurs masses étant respectivement 1000 et 3000 fois plus faibles que celle du Soleil. Il y a donc une énorme disproportion entre les attractions qu'exercent, sur la terre, par exemple, d'une part le Soleil, d'autre part l'ensemble des autres planètes. Il est facile de s'assurer que la force de gravitation qu'exerce Jupiter sur notre globe n'est guère que la 30.000^ème partie de l'attraction solaire.
Nous obtiendrons donc une représentation des mouvements célestes très proche de la vérité si nous supposons que les planètes qui gravitent autour du Soleil sont soumises seulement à son attraction, et si nous négligeons les forces qui s'exercent entre elles. En d'autres termes, le problème des mouvements planétaires se réduit, en première approximation, au problème des deux corps, chaque planète se mouvant par rapport au Soleil, comme si elle était seule. Ce problème a été résolu complètement par Newton; et l'on établit sans peine que l'orbite de la planète est une ellipse, dont le Soleil occupe un foyer [...]. On retrouve ainsi, par une voie déductive, les lois que Képler avait établies, au débur du XVII^ème siècle, à l'aide des observations recueillies par Tycho Brahé."

A.Denjon, Le Centenaire de la Découverte de Neptune (1946)

Ce petit travail est celui que l'on fait effectuer à un étudiant de première année, qu'il soit à l'université ou en classe préparatoire. On regarde Mars danser avec le Soleil, Mars décrit une ellipse; puis Jupiter danser avec le Soleil, et Jupiter décrit une ellipse; et ainsi il imprime le même mouvement à ses 7 partenaires, de Mercure à Uranus en passant par la Terre.
Mais la danse d'Uranus est bien troublante pour les astronomes! En fait, elle est plutôt troublée...

"Newton avait donné à son principe une généralité [dont] il fallait maintenant déduire les conséquences, et les poursuivre dans l'examen détaillé du système du monde. La première de ces conséquences fut que les lois de Képler ne pouvaient pas représenter exactement les mouvements réels des planètes. Considérons en effet une des planètes; elle est attirée vers le Soleil conformément à la loi de la gravitation. Newton a prouvé qu'en vertu de cette force elle doit décrire une ellipse autour du Soleil comme foyer [...] ; les lois de Képler seraient donc observées; mais la planète n'est pas soumise à cette seule attraction du Soleil; elle est attirée en outre par toutes les autres planètes; sous l'influence de ces forces à chaque instant variables, son mouvement réel ne sera donc pas elliptique, il sera d'une nature nécessairement très compliquée [...].
La première circonstance, qui facilite les approximations, est la prépondérance du Soleil dans le système planétaire [...]. Les distances mutuelles des planètes prises deux à deux ne devenant jamais très petites, on voit que l'attraction de deux planètes l'une sur l'autre ne sera jamais qu'une petite fraction de celle que le Soleil exerce sur chacune d'elles [...] .
Puisque, dans notre système, l'attraction du Soleil est partout répondérante, il est bien naturel de la considérer à part; à elle seule, elle ferait décrire à une planète indéfiniment la même ellipse; c'est là une approximation du mouvement réel; c'est cette approximation que Képler a déduite des observations de Tycho-Brahé.
Les petites forces provenant des actions des autres planètes seront des forces perturbatrices [...] ; cet effet est désigné sous le nom général de perturbations. "

F.Tisserand & H.Andoyer, Leçons de Cosmographie (1912)

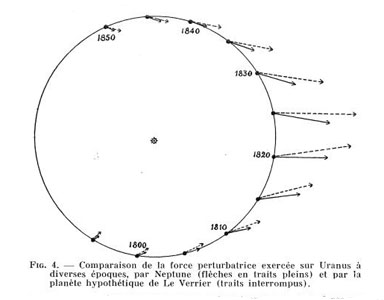
Sur les figures ci-dessous, on a visualisé la force d'attraction de Jupiter sur Mars, toujours portée par la droite qui les joint à un instant donné. Elle tend à déformer l'ellipse (en fait, presqu'un cercle!) de Mars en la tirant (légèrement) vers l'extérieur dans le cas rouge, et vers l'intérieur dans le cas vert. Dans ce deuxième cas, toutefois, la déformation sera moindre, car, les planètes étant plus éloignées l'une de l'autre, la force verte est nettement moins intense que la rouge d'après la loi de Newton (on na pas cherché à les représenter à l'échelle)

Ce travail (dans notre cas, appliquer à Mars la correction de l'action de Jupiter), les astronomes savent le faire: c'est certes fastidieux (cela l'est moins aujourd'hui, avec des ordinateurs): on connait le mouvement de Jupiter (on peut, en simplifiant un peu, le supposer elliptique, car peu influencé par les autres), on calcule la force pour un grand nombre de ses positions, et on corrige ainsi l'orbite de Mars.

Mais si l'astronome veut rechercher si une nouvelle planète -appelons la tout de suite Neptune!- agit de même sur Uranus, il doit résoudre un problème différent, qu' on peut qualifier de problème inverse: à partir des forces pertubatrices (évaluées en déduisant les perturbations déja connues, comme celle de Saturne, par exemple), déterminer "d'où elles viennent" pour localiser la nouvelle planète et son mouvement!

" L'existence d'une planète encore inconnue se trouvant ainsi mise hors de doute, j'ai renversé le problème qu'on s'est, jusqu'ici, proposé dans le calcul des perturbations. Au lieu d'avoir à mesurer l'action d'une planète déterminée, j'ai dû partir des inégalités reconnues dans Uranus, pour en déduire les éléments de l'orbite de la planète perturbatrice; pour donner la position de cette planète dans le ciel, et montrer que son action rendait parfaitement compte des inégalités apparentes d'Uranus."

U. Le Verrier, Note aux Comptes Rendus de l'Académie des Sciences (01/06/1846)

illustration tirée de: A.Denjon, Le Centenaire de la Découverte de Neptune (1946))
les forces perturbatrices telles qu'évaluées par Leverrier (pointillés) et réelles, telles qu'on apu les calculer 100 ans après.

Le Verrier au Travail

Une fois ce principe posé, rien n'est encore facile pour autant. Pour l'essentiel, méthode et rigueur sont les caractéristiques de son raisonnement; ainsi, nous les voyons à l'œuvre pour réfuter toutes les causes possibles du "trouble", sauf la bonne: il s'agit pour lui de démontrer, quasi mathématiquement!

" Les inégalités particulières d'Uranus seraient-elles à un gros satellite qui accompagnerait la planète? Les oscillations qui se manifesteraient dans la marche d'Uranus affecteraient alors une très courte période; et c'est précisément le contraire qui résulte des observations. [...]
Serait-ce donc une comète qui [...] aurait, à une certaine époque, changé brusquement la grandeur et la direction de son mouvement? [...] Mais alors, la prériode des observations de 1781 à 1820 pourrait se lier naturellement, soit à la série des observations antérieures, soit à la série des observations postérieures, et ne serait incompatible qu'avec l'une d'entre elles. Or, c'est ce qui n'a pas lieu. [...]
Il ne nous reste ainsi d'autre hypothèse à essayer que celle d'un corps agissant d'une manière continue sur Uranus, changeant son mouvement d'une manière très lente. Ce corps, d'arès ce que nous connaissons de notre système solaire, ne saurait être qu'une planète [...]
Et d'abord, on ne saurait la placer en dessous de Saturne, qu'elle dérangerait plus qu'elle ne trouble Uranus; et l'on sait que son influence sur Saturne est insensible.
Peut-on la supposer située entre Saturne et Uranus? Il faudrait la placer beaucoup plus près de l'orbite d'Uranus que de celle de Saturne et dès lors sa masse devrait être assez petite pour ne produire sur Uranus que des pertubations qui sont, en définitive, peu considérables. Il est facile d'en conclure que son action perturbatrice ne s'exercerait qu'au moment où elle passerait dans le voisinage d'Uranus [...]. Cette conséquence est contraire à ce qu'on déduit des observations.
La planète perturbatrice sera donc située au delà d'Uranus."

U. Le Verrier, Note aux Comptes Rendus de l'Académie des Sciences (01/06/1846)

Cependant, quelques obstacles sur la route ne laisseront d'autre choix à Le Verrier que de renoncer ou compléter par une hypothèse qu'il espère raisonnable, sans pour autant avoir de certitude, mais la Fortune va sourire à l'audacieux. Voyons quels "risques calculés" il prend.

L'évaluation des forces d'attraction gravitationnelle, dans son "problème inversé", demande de connaître la distance de la "planète troublante" et sa masse. Pour la première, il a recours à une loi empirique, dite de Titius-Bode, qui stipule que les écarts entre les planètes successives connues sont doublés par rapport au précédent; il l'extrapole à son inconnue et consolide l'argumentation par une estimation de son influence, comparée aux observations. Ensuite, partant du constat que les planètes connues décrivent leur orbite dans le plan de l'écliptique, ou presque, il pose pour principe qu'il en est de même pour sa planète inconnue. Extrait de ses déclarations:

" Nous savons, par la singulière loi qui s''est manifestée entre les distances moyennes des planètes au Soleil, que les planètes les plus éloignées sont situées à des distances qui sont, à très peu près, doubles les unes des autres; il serait donc naturel d'admettre que le nouveau corps est deux fois plus éloigné du Soleil qu' Uranus[...]. J'ai dit que la planète cherchée ne pouvait être située à une petite distance d'Uranus. Or, il n'est pas plus possible de la placer à une très grande distance, à une distance triple de celle d'Uranus au Soleil par exemple. Il faudrait en effet, dans cette hypothèse, attribuer à cette planète une masse très considérable [...] et il ne serait point possible d'expliquer les inégalités d'Uranus sans développer dans Saturne des perturbations très sensibles, dont il n'existe point de traces.
Ajoutons que les orbites de Jupiter, Saturne et Uranus étant fort peu inclinées à l'écliptique, on peut admettre, dans une première approximation, qu'il en est de même pour la planète cherchée; [...]"

U. Le Verrier, Note aux Comptes Rendus de l'Académie des Sciences (01/06/1846)

La masse est la question la plus délicate. Elle sera facile à déduire de la loi de Newton... le jour où l'on connaîtra une lune de la nouvelle planète, on est loin d'en être là! Le Verrier va s'en tirer avec une belle ingéniosité, en la "confinant" dans un terme correctif où elle intervient par son inverse. Ainsi, son influence se bornera à ouvirir plus ou moins l'éventail autour d'une première position.

"Il est fort remarquable que la masse ait, à très peu près, disparu d'elle-même de ces équations. L'élimination de l'excentricité et de la longitude du périhélie entraîne, non pas l'évanouissement complet des termes dépendant de la masse, mais leur réduction à un tel degré de petitesse, qu'il devient évident que cette masse ne pourra point être déterminée avec précision, qu'il sera permis de la supposer comprise entre des limites assez étendues. [...]
En disant que le problème n'est susceptible que d'une solution, j'entends qu'il n'y a pas deux régions du ciel que l'on puisse choisir à volonté, pour y placer la planète à une époque déterminée, au 1er janvier 1847 par exemple. Mais chacun comprendra que, dans cette région unique, on doit se borner à assigner à la position de l'astre certaines limites [...]"

U. Le Verrier, Note aux Comptes Rendus de l'Académie des Sciences (01/06/1846)


Calculs pour Neptune: du manuscrit...	... à l'article publié aux Comptes-Rendus de l'Académie des Sciences

L'article ne reproduit aucun des volumineux calculs qu'il a eu à faire. Mais, en dépit du temps et de la sueur dépensés, il est remarquable que, dans sa conclusion, loin de se satisfaire du résultat, Le Verrier annonce qu'il va perfectionner son étude

"Le travail dont je viens de présenter un extrait à l'Académie doit être considéré comme une ébauche d'une théorie qui commence. [...]Je vais m'occuper d'apporter à la nouvelle théorie les perfectionnements dont elle est susceptible."

U. Le Verrier, Note aux Comptes Rendus de l'Académie des Sciences (01/06/1846)

C'est qu' en fait, il était pressé de publier pour prendre date, puisqu'il sait qu'en Angleterre, il a un concurrent. Dans sa nouvelle mouture, trois mois plus tard seulement, il s'affranchit de la loi de Titius-Bode et utilise toutes les observations, mais en les regroupant pour obtenir un problème "de taille raisonnable": 33 équations pour 9 inconnues!

"Guidé par des considérations particulières et par quelques essais, j'avais admis, dans ma première solution, que le grand axe de l'orbite de la planète cherchée était double du grand axe de l'orbite d'Uranus; j'avais ensuite fait voir quavec cette hypothèse [...], on pouvait satisfaire aux équations du problème. C'était une solution détournée. Dans le travail actuel, la valeur la plus exacte du grand axe est, comme celle des autres éléments, déduite directement des équations [...]"

"Lorsque j'ignorais complètement dans quelle partie du zodiaque se trouvait le nouvel astre, et qu'il me fallait, par conséquent, étendre mes recherches à toutes les régions de l'écliptique, j'avais dû, pour ne pas rendre les discussions interminables, me borner à l'emploi d'un certain nombre d'observations d'Uranus convenablement choisies. Dans le travail actuel, je fais usage [...] de toutes les anciennes observations d'Uranus, au nombre de dix-neuf, faites par Flamsteed, Bradley, Mayer et Lemonnier; et j'emploie le nombre considérable de deux cent soixante deux observations, choisies convenablement parmi celles qui ont été faites à Paris et à Greenwich, depuis 1781 jusqu'en 1845[...]. Chacune des longitudes déduites des observations, comparée avec la longitude donnée à la même époque par la théorie, fournit une équation de condition entre les corrections des éléments de l'orbite d' Uranus, entre la masse et les éléments de l'orbite cherchée. Ces équations renferment ainsi neuf inconnues [...]

Il n'est pas nécessaire de traiter séparément chacune des équations ainsi formées. La lenteur du mouvement d'Uranus, et celui de la planète perturbatrice, permettent d'en réunir plusieurs, de manière à former des équations moyennes, dont les constantes seront probablement d'autant plus exactes, qu'elles résulteront de l'emploi d'un plus grand nombre d'observations.[...]"

U. Le Verrier, Note aux Comptes Rendus de l'Académie des Sciences (31/08/1846)

Encore du travail, des calculs, mais la conclusion est triomphale:


" Cette longitude vraie diffère peu de 325°, valeur qui résultait de mes premières recherches [...] elle place le nouvel astre à 5 degrés environ à l'est de l'étoile Delta du Capricorne."

Il n'a plus qu'à écrire aux responsables des divers observatoires d'Europe pour leur communiquer la position calculée.

l'observatoire de Berlin

" Aujourd'hui, je voudrais obtenir de l'infatigable observateur qu'il voulût bien consacrer quelques instants à l'examen d'une région du Ciel, où il peut rester une planète à découvrir. C'est la théorie d'Uranus qui m'a conduit à ce résultat.
Vous verrez, Monsieur, que je démontre qu'on ne peut satisfaire aux observations qu'en introduisant l'action d'une nouvelle planèrte, jusqu'ici inconnue: et ce qui est remarquable, il n'y a dans l'écliptique qu'une seule position qui puisse être attribuée à cette planète perturbatrice. Voici les éléments de l'orbite que j'assigne à cet astre:

[ ici, Le Verrier donne les mêmes éléments que dans sa communication à l'Académie. ]

La position actuelle de cet astre montre que nous sommes actuellement, et que nous serons encore, pendant plusieurs mois, dans des conditions favorables pour la découvrir."

U. Le Verrier, Lettre à Galle (18 Septembre 1846)

La Confirmation

Elle vient, presque par retour du courrier, de Berlin. Dans la nuit du 2 au 24 septembre, Galle trouve la planète non loin de la position suggérée:


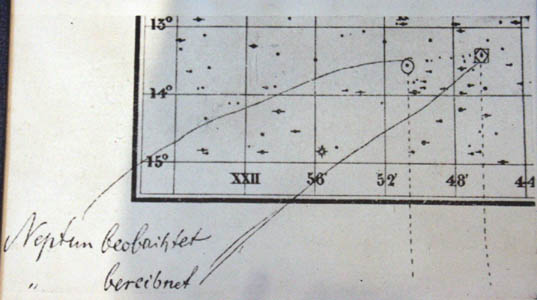
Lettre de Galle à Le Verrier	Relevé des positions, par Galle. bereitnet = préparée (par le calcul); beobachtet = observée

Neptune -qui ne porte pas encore ce nom!- est observée à Paris par Le Verrier lui-même, à Vienne, Genève, à Göttingen par Gauss en personne, à Saint-Petersbourg d'où il reçoit de chaleureuses félicitations.


Otto Struve...	...félicite Le Verrier...	...au nom de son père, directeur...	... de l'Observatoire de Poulkova (Saint-Petersbourg)

LeTriomphe

Sa célébrité est non seulement immédiate, elle est immense. Car elle dépasse rapidement le petit cercle scientifique pour gagner le grand public: jusqu'à sa mort, il personnifiera l'astronomie dans les journaux, l'imagerie populaire... jusqu'au fond des plaques de chocolat!

Un projet d'allégorie retraçait toute l'épopée, la faisant commencer à Laplace, dont la monumentale Mécanique Céleste avait codifié, comme personne avant lui, le calcul des perturbations. Cette décoration en trompe-l-'œil ne fut toutefois jamais réalisée.

Edmond Louis Dupain, "Le Verrier découvre la planète Neptune", projet pour un plafond à l'Observatoire (1889).
(cliquer pour une image aggrandie sans les indications)

La Contestation

Le Verrier avait en Angleterre un challenger... qui avait même quelques longueurs d'avance. Mais à cause d'une demande complémentaire d'Airy, qui n'était pas de première urgence, et de la négligence de l'astronome effectuant les observations à Greenwich, Challis, plus préoccupé par sa chasse personnelle aux comètes, il ne publie pas le premier, alors qu'il était en mesure de le faire.
Il est intéressant d'observer qu'il "comble les trous" du raisonnement comme Le Verrier: utilisation de la loi de Titius-Bode, localisation dans le plan de l'écliptique (avec toutefois un argument scientifiquement plus fort)

" Un jeune étudiant de 23 ans, John Couch Adams, [allait] aborder cette tâche redoutable. Il se l'était assignée dès l'âge de 21 ans, en un memorandum que l'on conserve à Cambridge. [...]

Devenu fellow de Saint John College, à Cambridge, il imagine une méthode d'approximation à la fois simple et élégante pour calculer les inconnues, non sans avoir judicieusement réduit, au préalable, le nombre de celles-ci. Tout d'abord, la planète cherchée ne produisant pas de perturbations sensibles sur la latitude d'Uranus, il est permis de la supposer dans l'écliptique[...]. D'autre part, la détermination du grand axe de la planète troublante soulevant, comme on l'a dit, des difficultés insurmontables, Adams avait fait à son sujet une hypothèse vraisemblable en le suposant double de celui d'Uranus. En effet, la même relation existe, approximativement, entre les orbites de Saturne et Jupiter et celles d'Uranus et Saturne. Adoptant pour cette inconnue la valeur 38, Adms n'a plus que 8 quantités à déterminer. Après deux années de travail, il est en mesure de communiquer à Airy, Astronome Royal, les éléments elliptiques et la position de la planète cherchée. Sa note, datée de de 1845, montrait que, dans la nouvelle théorie, les écarts entre les positions observées d'Uranus et les positions calculées étaient réduits à moins de 2" pour la période postérieure à 1781 [...]

Airy, absent de Greenwich lorsque Adams s'y était présenté, répondit au début de novembre, en demandant si la théorie qui corrigeait si bien, en longitudes, les erreurs des tables, corrigeait également les erreurs du rayon vecteur. [...]

Mais Adams ne répondit pas, et sa correspondance avec Airy ne reprit qu'en 1846."

A.Denjon, Le Centenaire de la Découverte de Neptune (1946)

St-John College, Cambridge (Angleterre): portail d'entrée, et vu depuis les jardins.

"Il y a longemps, probablement en 1844 ou au début de 1845, j'ai fourni à M. Adams des observations d'Uranus, expressément pour ses recherches sur la cause des perturbations.
En octobre ou novembre 1845, j'ai reçu de M. Adams la notification que les perturbations d'Uranus pourraient être expliquées en supposant l'existence d'une autre planète, dont il l'a donné les éléments.
Peu après, je lui ai demandé les mêmes éclaircissements qu'à vous. Je ne sais si M. Adams a bien reçu ma lettre: en tout cas, il ne m'a pas répondu. L'aurait-il fait, je l'aurais immédiatement poussé à publier ses résultats.
En juin 1846, j'ai reçu le numéro des Comptes Rendus contenant le résultat de vos investigations: j'ai été stupéfait et ravi de constater que les éléments étaient sensiblement les mêmes, et que l'emplacement de la planète était voisin de celui que M. Adams avait prédit."

G. Airy, Lettre à Le Verrier (19/10/1846)

Enfin rédigé en 1846, le travail d'Adams ne fut publié qu'en 1851 dans le Nautical Almanac britannique; et traduit en 1876 seulement pour le journal de Liouville, mais dans une révision de l'auteur.

" Mon attention fut, pour la première fois, dirigée sur ce sujet, il y a quelques années, par la lecture de l'excellent rapport de M. Airy, sur les progrès de l'Astronomie. Je trouve dans mes papiers la Note suivante datée du juillet 1841: «Formé le projet, au commencenment de cette semaine d' étudier aussitôt que possible, après avoir pris mon grade, les irrégularités dans le mouvement d'Uranus qui restent encore inexpliquées, à l'effet de trouver si l'on doit les attribuer à l'action d'une planète plus éloignée et non encore découverte et, s'il est possible, de déterminer approximativement les éléments de son orbite [...] Donc, en 1843, je tentai une première solution du problème, en supposant que l'orbite fût un cercle avec un rayon égal à deux fois la distance moyenne d'Uranus au Soleil. [...]
En novembre 1845, M. Le Verrier présenta à l'Académie royale des Sciences de Paris une étude très complète et très détaillée des perturbations d'Uranus [...]. Au mois de juin [1846] il a fait suivre son étude d'un Mémoire dans lequel il a attribué les perturbations à l'action d'une planète deux fois plus éloignée du Soleil quUranus. [...] Le 31 août il a présenté à l'Académie une étude plus complète [...] Je mentionne ces dates uniquement pour montrer que mes résultats ont été obtenus indépendamment cde eux de M. Le Verrier et avant qu'il eût publié les siens; je n'ai d'ailleurs pas l'intention de lui disputer l'honneur de cette découverte, car il est hors de doute que ses résultats ont été publiés les premiers [...] »

J.C.Adams, Explications des Inégalités observées dans le Mouvement d'Uranus (1876)
disponible en ligne: partie 1, partie 2.

Cette antériorité indiscutable, mais non actée par une publication, est à l'origine de polémiques dans et entre les deux pays: en Angleterre, l'opinion publique reproche à Airy et à Challis, directeur de l'observatoire de Cambridge, leur manque de réactivité, voire leur négligence de ne pas avoir poussé Adams à publier, même un résultat incomplet, et donc de s'être fait voler la primeur par les Français; en France, on accuse les Anglais d'être mauvais perdants et de vouloir récupérer le prestige de la découverte: les voleurs, ce sont eux!

Caricature de Cham dans L'Illustration: Adams découvre Neptune...
en observant à la lunette la publication de Le Verrier, par dessus la Manche!

Pour ne rien arranger, voilà que l'astronome (anglais) William Lassel découvre un premier satellite de Neptune, Triton, 17 jours seulement après l'observation de Galle. Or, c'est justement ce qui permet, ne vertu de la loi d'attraction universelle, de déterminer assez précisément la masse de Neptune: dans ce calcul, c'est celle du satellite qui s'élimine, pas celle du centre d'attraction. Et de découvrir que Le Verrier l'a mal évaluée (Adams aussi, d'ailleurs), et dans la foulée de l'accuser d'habiller de la rigueur des calculs une découverte chanceuse. Ce bouillonement finira par se calmer; d'ailleurs les deux principaux intéressés entretiendront toujours des relations cordiales.

Pour plus de détails, notamment des correspondances retrouvées des acteurs anglais de cette histoire... anglaise, on consultera avec interêt les pages de Nick Kollerstrom.

Trouver par le calcul... un précédent?

Quelqu'un avait déjà fait sensation en disant aux astronomes dans quelle portion du ciel pointer leur lunette... ni plus ni moins que Gauss en personne!
Il ne s'agissait pas, il est vrai, de découvir... seulement de retrouver la planète naine Cérès, située entre Mars et Jupiter, à la distance suggérée, une fois de plus, par la loi de Titius-Bode; L'Italien Piazzi avait été le premier à la voir, le 1^er Janvier 1801,et il l'avait suivie pendant 42 jours (19 observations) avant de la "perdre" dans la lumière du Soleil, leur placement mutuel étant défavorable.
Âgé de 24 ans seulement, Gauss réalisa en octobre 1801 les calculs qui permirent de retrouver Cérès dans les objectifs des télescopes. Théoriquement, 3 positions, chacune avec 2 angles, suffisent pour déterminer les 6 paramètres d'une orbite elliptique; mais il faudrait, pour un bon résultat, que ces positions soient assez différentes sur l'orbite; au contraire les observations de Piazzi couvraient un angle d'à peine 3°. Conscient de n'avoir qu'un résultat grossier, Gauss détermina néanmoins de cette manière un premier jeu de valeurs.
Son idée maîtresse fut de les corriger en comparant positions observées et positions prédites dans le temps à partir de ces premières valeurs, en déterminant des corrections de façon à minimiser la somme des carrés des erreurs: c'est la méthode des mondres carrés, devenue universelle pour résoudre "au mieux" un système qui a trop d'équations: c'est bien le cas ici, avec 38 équations pour 6 paramètres. Le Verrier et Adams, comme on peut le lire ci-contre, ont eux aussi eu recours à cette méthode dans un contexte mathématique similaire.

page de J.C.Adams, Explications des Inégalités observées dans le Mouvement d'Uranus (1876), partie 1

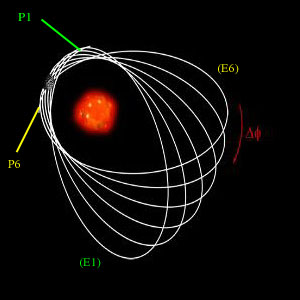
Pour plus de détails sur les calculs de Gauss relatifs à Cérès:
ce sujet proposé à l'analyse de candidats aux grandes écoles en 2009, cette présentation, ou ce texte plus fouillé.

Et pourquoi pas Mercure?

L'autre planète qui pose le plus de problèmes aux astronomes; c'est Mercure. On parle d'avance de son périhélie (point le plus proche du Soleil dans une trajectoire elliptique) parce que son mouvement est modélisé par une ellipse képlérienne qui tournerait lentement autour du soleil. Mais cela reste un mystère à l'époque, car l'influence de Vénus ne peut à elle seule expliquer toute la pertrubation.

Le vainqueur de Neptune cherche tout naturellement à se mesurer à ce nouveau défi. En 1859, il écrit à ce sujet à l'astronome Faye une lettre publiée auxc Comptes Rendus, constatant un écart inexpliqué par la théorie de Newton: 38" par siècle!
Il va de nouveau proposer ce qui a si bien réussi pour les perturbations d'Uranus: une planète troublante entre le Soleil et Mercure. Tout en concédant sa surprise qu'elle n'ait pas encore été aperçue... une méfiance qui se révèlera tout à fait justifiée.

mouvement du périhélie de Mercure,
annoté d'après une figure de ce site


relevés de Le Verrier à propos de Mercure	début de l'article de 1859

Le passage de Mercure devant le Soleil,
Giacomo Balla (1914)
Centre Georges Pompidou, Paris

" On dispose, dans l'espace d'un siècle et demi, d'un certain nombre d'observations de Mercure jouissant d'une grande précision: je veux parler des contacts internes du disque de Mercure avec le disque du Soleil, morsque la planète vient à passer devant cet astre. [...]. On possède, depuis 1697 jusqu'en 1848, vingt et une observations de cette espèce, auxquelles on doit pouvoir satisfaire de la manière la plus étroite si les inégalités des mouvements de la Terre et de Mercure ont bien été calculées, et si les valeurs attribuées aux masses perturbatrices sont exactes.[...]
Mais ce qui est remarquable, c'est qu'il a suffi d'augmenter de 38 secondes le mouvement séculaire du périhélie pour représenter toutes les observations des passages à moins d'une demi-seconde. [...]
Considérons, pour fixer nos idées, une planète qui serait située entre Mercure et le Soleil [...] la planète hypothétique devrait imprimer au périhélie de Mercure un mouvement séculaire de 38 secondes, et il en résulte, entre sa masse et sa distance au Soleil, une relation telle qu'à mesure qu'on supposera une distance plus petite, sa masse augmentera et inversement. [...]
Mais se pourrait-il qu'un tel astre existât sans jamais avoir été aperçu? [...] Comment admettre qu'on n'eût point été frappé de sa vive lumière durant quelqu'une des éclipses totales de Soleil? D'où vient qu'on ne l'ait jamais découvert passant sur le disque de cet astre?
Toutes les difficultés disparaîtraient en admettant, au lieu d'une planète, l'existence d'une série de corpuscules circulant entre Mercure et le Soleil. "

U. Le Verrier, Lettre à Faye (18 Septembre 1846)

Cette nouvelle planète demeurait invisible, mais on lui avait trouvé un nom: Vulcain! Le brio dont avait fait preuve Le Verrier pour révéler Neptune avait parfois rendu ses collègues abusivement enthousiastes (le deuxième cité n'est autre que le célèbre découvreur des cercles de Villarceau, sections bitangentes du tore!):

" Né au moment de l'apparition de la célèbre comète de 1811, il quitte la terre en s'ingéniant à fixer la route dun astre nouveau, de ce Vulcain à peine entrevu, dont il a su cependant relier avec une sérieuse probabilité les fugitives reconnaissances. Nous pouvons dire combien sa peine a été vive de le manquer de quelques jours dans le ciel."

H. Tresca (Bureau des Longitudes), Discours aux funérailles de Le Verrier (25/09/1877)

" Un résultat inattendu de ce grznd travail, fut la révélation de l'existence d'une planète intra-mercurielle, produisant, dans le mouvement de Mercure, des perturbations qu'on ne saurait expliquer sans déroger aux lois simples de la Mécanique céleste: la discussion des observations des petites taches circulaires qu'on a vues, sur le disque du Soleil, à diverses reprises, ne peut laisser aucun doute à cet égard; le prévisions de la théorie ne manqueront pas d'être confirmées par les observations décisives qui seront faites ultérieurement. La Science sera ainsi redevable au grand astronome que la mort vient de frapper des deux planètes qui commencent et finiddent lla série de ces astres "

Y. Villarceau (Observatoire de Paris), Discours aux funérailles de Le Verrier (25/09/1877)

Avec le temps et le recul, on sera plus cirtique... y compris sur une prétendue observation effective, qui avait enflammé Le Verrier:

" J'ai assisté à l'odyssée de cette curieuse histoire, étant alors élève astronome à l'Observatoire de Paris, et m'étant trouvé précisément en relation avec l'auteur de cette prétendue découverte, le docteur Lescarbault, d'Orgères. Le 26 mars 1859, cet excellent docteur, qui aimait passionément l'astronomie et en comprenait la grandeur, a bien réellement vu une tache ronde sur le Soleil, le matin, avant son départ pour ses visites médicales, et il la revit lorqu'il revint pour le déjeuner. Elle avait changé de place, mais ce déplacement était simplement dû au mouvement diurne apparent du Soleil [...]
À cette époque, M. Le Verrier, acharné à son grand travail sur le mouvement de la planète Mercure, publiait dans les comptes rendus de l'Académie des Sciences des conclusions numériques desquelles il paraissait ressortir que le mouvement de Mercure était troublé par une planète perturbatrice. C'était, en petit, la répétition de sa découverte de Neptune par les perturbations de la planète Uranus. M. Lescarbault signala son observation dans le journal Le Cosmos, et le directeur de l'Observatoire de Paris sauta dessus, pour ainsi dire avec enthousiasme. Il se rendit à Orgères, petite ville d'Eure et Loir, et arriva subitement chez le brave docteur pour lui demander à voir son registre d'observations. Ce registre n'existait pas. [...]La date de l'observation concordait avec les exigences de la théorie de Mercure; l'illustre astronome s'en déclara satisfait et fit décorer Lescarbault de la Légion d'honneur.
Cette petite planète, située entre Mercure et le Soleil, et baptisée du nom de Vulcain, aurait dû tourner en trente-trois jours autour de l'astre radieux. M. Le Verrier fit calculs sur calculs et annonça les dates auxquelles ses passages pourraient être observés. Jamais on n'a rien vu. Je me suis constamment élevé contre cette illusioj, qui dure encore. "

C. Flammarion, Mémoires Biographiques et Philosophiques d'un Astronome (Flammarion, 1911)

L'explication viendra d'ailleurs. Et, pour la première fois, pas de la mécanique de Newton, mais de la Relativité Générale, dont cela constituera, d'ailleurs, la première vérification expérimentale. Albert Einstein l'a publiée en 1915, mais, de son propre aveu, c'est en 1912, lors de son séjour à Prague, qu'elle a été conçue pour l'essentiel. C'est dans un de ces trois endroits que s'est dénoué l'intrigue qui aura fait buter Le Verrier!


Institut de Physique Théorique	sa maison, rue Lesnická (détail)	son café préféré, au centre ville

Le traité que publiera Einstein mentionne explicitement la tentative de Le Verrier en 1859.

A. Einstein, la Théorie de la Relativité restreinte et générale (1921)

Une Neuvième Planète?

" Il ne viendra sans doute à personne l'idée de vouloir réduire notre système solaire à d'étroites limites, et d'en tirer une conclusion contre l'existence dun nouvel astre. Dans ce cas, cependant, je répondrais qu'on aurait eu les mêmes raisons d'affirmer, le 12 mars 1781, que Saturne était la dernière des planètes, sauf à être contredit le lendemain par la découverte d'Uranus. L'hypothèse qu'il existe des planètes plus éloignée du Soleil que celles que nous connaissons est-elle donc neuve? Dès l'année 1758, l'illustre géomètre Clairaut déclarait, à l'occasion des perturbations dela comète de Halley, qu'un corps qui traverse des régions aussi éloignées pourrait être soumis à des forces totalement inconnues, telles que l'action de planètes, trop distantes pour être jamais aperçues.
Espérons seulement que les astres dont parle Clairaut ne seront pas tous invisibles; que, si le hasard a fait découvrir Uranus, on réussira bien à voir la planète dont je viens de faire connaître la position. "

U. Le Verrier, Note aux Comptes Rendus de l'Académie des Sciences (01/06/1846)

La conclusion de Le Verrier , reprenant Clairaut, est intéressante: elle ne referme pas le système solaire à sa nouvelle découverte... de fait, c'est l'étude des perturbations de... Neptune qui fit découvrir une neuvième planète dans le système solaire en 1930: Pluton.

Las! Elle a perdu ce statut en 2006 (pour de bonnes raisons astronomiques), et le premier des assassins (nous ne lui faisons pas injure, puisque c'est ainsi qu'il l'humour de se définir dans son livre ci-contre) s'appelait Mike Brown...

Or voilà qu'en 2016, le même, avec de non moins solides raisons, envisage très sérieusement une nouvelle neuvième planète dans notre système solaire, décidément jamais tranquille. D'où vient ce soupçon? Encore et toujours de perturbations détectées sur des objets de la ceinture de Kuiper, dont fait partie la planète naine Pluton. Mike Brown qualifie cette hypothétique planète 9 de « perturbateur massif ».
Développer ici ce sujet nous écarterait trop, mais il est intéressant de voir que l'étude des perturbations n'a rien perdu de son intérêt: Neptune, Vulcain, et Fattie (sobriquet affectueux pour cette géante gazeuse... imposante si elle existe) nous promènent de succès en échec et en interrogation! Pour rester informés:

Konstantin Batygin and Michael E. Brown, Evidence for a Distant Giant Planet in the Solar System (texte)
Konstantin Batygin, Planet Nine from Outer Space (conférence vidéo à voir absolument, pour son historique incluant Le Verrier!)
Mike Brown, Blog Planet Nine

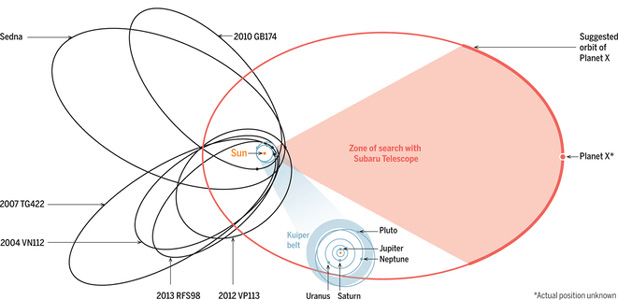
Sur la figure ci-contre, on remarque la très forte excentricité de la planète chassée.

Le système connu, jusqu'à Pluton, est situé dans le petit cercle bleu autour du soleil; le déplacement vers le bas est un effet de loupe de l'auteur du croquis, pour agrandir cette zone: sinon, il ne pourrait représenter en respectant l'échelle les orbites connues et celle de la planète 9.
Les autres orbites allongées (en noir) sont celles d'objets transneptuniens déjà identifiés, comme Eris ou Sedna (ce sont des planètes naines, alors que la planète 9 a une masse estimée à 10 fois celle de la terre)

Références

Articles Historiques de Le Verrier... et Adams

Sur les Variations Séculaires des Éléments Elliptiques des Sept Planètes Principales (JMPA série 1, t.5, 1840)
Mémoire sur les Variations Séculaires des Éléments des Orbites... in Connaissance des Temps pour l'Année 1843
Premier Mémoire sur la Théorie d'Uranus (CRAS série 1, t.21,1845; séance du 10 novembre)
Recherches sur les Mouvements d'Uranus (CRAS série 1, t.22, 1846)
Sur la Planète qui produit les Anomalies Observées dans les Mouvements d'Uranus (CRAS série 1, t.23, 1846)
Sur la Planète Neptune (CRAS série 1, t.27, 1848)
Recherches Astronomiques, Chapitre XV: Théorie de Mercure (Annales de l'Observatoire Impérial de Paris, t.5, 1859)

J.C. ADAMS, Explications des Inégalités observées dans le Mouvement d'Uranus, partie 1, partie 2 (JMPA série 3, t.2, 1876)

Analyses sur BibNum d'articles de Le Verrier

A. JUHEL, Le Verrier et le Premier Calcul de Valeurs Propres (sur l'article [1] )
J. LEQUEUX, La découverte de Neptune (1846) (sur les articles [4] et [5])

Articles Divers

A. DANJON, Le Centenaire de la Découverte de Neptune in Ciel et Terre, Vol. 62 (1946)
A. DANJON, La Découverte de Neptune in Bulletin de la Société Astronomique de France, Nov/Dec 1946
S. VOISIN, J. CHANTIER, Neptune : quand le Calcul précède l’Observation (Blog Gallica, 2016)
E. SANCHEZ-PALENCIA, La découverte de Neptune et le fiasco de Vulcain (site de l'Académie desSciences)
F.-F. TISSERAND, Les Travaux de Le Verrier in Annales de l'Observatoire Impérial de Paris, t.15, 1880
N. KOLLERSTROM, Neptune's Discovery: the British Case for Co-Prediction
J.-M. SOURIAU, Une Méthode pour la Décomposition Spectrale et l'Inversion des Matrices (CRAS 227, 1948)
WIKIPEDIA, articles Neptune et Découverte de Neptune

Ouvrages Divers

F.-F. TISSERAND, H. ANDOYER, Leçons de Cosmographie (1912), disponible sur Gallica (BnF)
D.K. FADDEEV, V.N. FADDEEVA, Computational Methods of Linear Algebra (Freeman, 1963)
É. DURAND, Solutions Numériques des Équations Algébriques, vol 2 (Masson, 1961)
M. SIBONY, J.-C. MARDON, Analyse numérique t.1 : Systèmes Linéaires et non Linéaires (Hermann, 1984)

et toujours, la référence exhaustive:

J.LEQUEUX, Le Verrier, Savant Magnifique et Détesté (EDP Sciences)

Pour en savoir plus sur cet ouvrage, une mini-interview de l'auteur sur le site lechoixdeslibraires.com

Revenir à la Page biographique de Le Verrier

Revenir à la Page de l'Observatoire

Revenir à la Home Page du Mathouriste