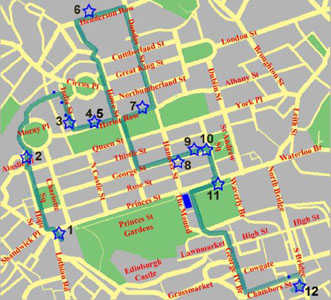
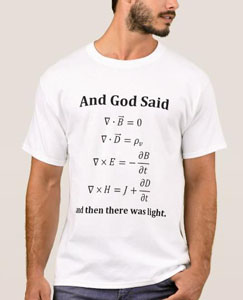Maxwell à Édimbourg
Au pied du château d'Édimbourg s'étend la "ville nouvelle", sorte de pré-Manhattan imaginé en 1766 par un jeune architecte de 22 ans, James Craig. Il dessine, en urbaniste des Lumières,
trois grandes artères et de larges rues à la
perpendiculaire. C'est dans ce quartier que naît en 1831 celui
dont on dit qu'il apporta la lumière au monde en quatre
équations magistrales: James Clerk Maxwell.
Et c'est en 2008 que fut inaugurée sur la principale de ces artères, George Street, un monument par lequel son Écosse natale lui rend hommage. Il aurait été difficile de trouver un emplacement mieux approprié: dans son quartier de naissance, au début de la plus grande rue, dans laquelle se trouve, non loin de là, le bâtiment de la Royal Society of Edinburgh, commanditaire de la statue - il en fut un membre éminent. La rue qui passe dans son dos fait face au grandiose monument néogothique dédié à Walter Scott, emblème de l'Écosse littéraire; Maxwell occupe, dans les sciences physiques et mathématiques, une place analogue. Quand on veut résumer la physique à trois géants, ils se nomment, par ordre chronologique: Newton, Maxwell et Einstein. Or, Maxwell est très exactement celui qui fera basculer la physique de son ancien monde, celui de la perfection newtonnienne, au nouveau monde relativiste incarné par Einstein.
Il vaut mieux être préalablement averti de sa
localisation, tant les signes distinctifs sont discrets: entre les deux
fenêtres, une pierre de la façade a été
gravée pour rappeler sa date de naissance en ce lieu; et si la
sonnette indique que la maison est le lieu d'un petit musée et
le siège de la James Clerk Maxwell Foundation... impossible d'en voir plus, sans faire partie d'un groupe constitué qui a pris un rendez-vous préalable!
Une troisième plaque a été apposée, juste à droite de la sonnette. Son cuivre lui si fort qu'on peine à lire de face, et qu'en inclinant un peu son angle de visée on y voit surtout... les maisons d'en face, inlassablement du même modèle. Fort heureusement, les mathématiques peuvent nous tirer de ce mauvais pas: il suffit d'augmenter encore plus l'angle de visée (donc de déformer beaucoup plus, dans un premier temps!) avant de... redresser l'image grâce à une transformation géométrique matricielle. La chose est gérée intuitivement, à la souris, par de nombreux logiciels de retouche: le Mathouriste a, par exemple, utilisé Gimp, logiciel libre. Et voici le résultat, à droite! Vous n'avez plus qu'à méditer l'avis d'Einstein sur Maxwell...

Trinity College, Cambridge. À gauche, la chapelle.
... et son imposante chapelle, pour rendre hommage aux statues
d'Isaac Newton et Francis Bacon. Voici un peu de ce qu'a dû
ressentir le jeune James, car la sollenité du lieu est
restée intacte et impressionne tout autant le visiteur
contemporain.
Au bout d'un trimestre, il migre à Trinity. On s'y entraîne frénétiquement au célèbre examen, les Mathematical Tripos, qui certes requièrent virtuosité, rapidité et habileté, mais reposent sur un corpus fort peu moderne, dont les Éléments d'Euclide demeurent l'alpha et l'oméga. Maxwell compare l'entraînement à un apprentissage du jonglage et s'en acquitte assez consiencieusement pour être classé deuxième; le major, ou Senior Wrangler comme il est de tradition de l'appeler, est un autre futur grand mathématicien, Edward Routh (surtout connu pour son critère de stabilité des systèmes contrôlés, toujours très utilisé en ingéniérie).
Il enseignera ensuite la physique à Aberdeen (plus de détails dans ce texte), à Londres au King's College (1860-65: plus de détails dans ce texte), poste auquel il renoncera pour retourner dans sa chère Écosse, à son domaine de Glenfair. C'est là qu'il donnera naissance, en 5 ans, à la théorie électromagnétique qui va révolutionner la science et les techniques.
Il reviendra à Cambridge pour fonder et prendre la tête du Cavendish Laboratory de l'université (plus de détails dans ce texte); et c'est là qu'il mourra en 1879, âgé seulement de 48 ans.
Au premier coup d'œil, on le daterait volontiers du XIXème siècle, tant il est conforme aux canons de cette époque: reproduction fidèle, pause très académique, évocation de ses principaux travaux, dans sa statue que dans les plaques du socle... pourtant, il a été réalisé au XXIème siècle! Par un artiste qui, non seulement est considéré, mais se revendique lui-même comme un néo-classique: Alexander Stoddart.
Deux photographies ont visiblement inspiré le sculpteur: dans la première, le grand physicien pose avec, à ses pieds, son terrier favori, Toby -probablement inspiré par une photographie célèbre (quoique d'auteur inconnu). On aime bien les chiens, dans la sculpture écossaise: outre le célèbre Greyfriars Bobby, celui de Walter Scott est représenté aux pieds de son maître!
Dans la seconde, on le voit tenir le disque à tranches colorées qui lui a servi à faire la démonstration de la synthèse de la lumière blanche à partir de ses composantes de couleur (grâce à la permanence rétinienne, l'œil perçoit la somme de toutes les couleurs), opération inverse de l'analyse de cette même lumière, décomposée par Newton dans sa célèbre expérience du prisme. Analyse et synthèse du signal lumineux: nous voici déjà, par l'expérience, en pleine théorie de Fourier, sur laquelle nous verrons Maxwell exprimer son enthousiasme un peu plus loin.
Les bas-reliefs du socle situent la place de Maxwell dans la
physique: entre Newton et Einstein, mais tellement "à l'antique"
qu'il faut être préalablement averti, puis
particulièrement attentif aux détails pour saisir
l'allégorie. À la gauche de Maxwell, les prismes
évoquent Newton et son travail sur la lumière; à
sa droite, c'est bien à Einstein qu'il est fait allusion, par le
biais d'une masse (ici, une boule!) qui déforme l'espace-temps.
À l'arrière, deux plaques: une grande indique les nombreuses instituions scientifiques dont Maxwell était membre; sur la petite sont gravées les quatre fameuses équations de l'électromagnétisme, reprises de manière plus visible à l'avant du monument, insérées au milieu des pavés.
La souscription a été lancée en 2006 par la RSE et son président, Sir Michael Atiyah; voir la plaquette des donateurs et un poème inspiré par la statue.
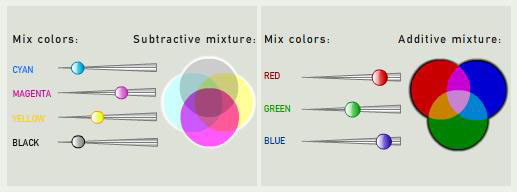
Puisque les pigments se composent par soustraction, vous ne serez plus surpris de voir, dans votre imprimante, trois cartouches des couleurs opposées aux couleurs de synthèse additive de l'écran: cyan, jaune et magenta!
Une démonstration des deux synthèses est proposée dans cette page, où les curseurs de l'image reproduite ci-dessous sont mobiles à la souris, et le résultat immédiatement visible, histoire de vérifier que vous avez bien tout compris.
De très nombreuses références complémentaires sur la couleur sont disponibles ici.
Maxwell ne pouvait deviner, avec plus de 100 ans d'avance, ce succès universel de son triangle... ainsi en va-t-il des travaux des grands précurseurs! Il assula en revanche pleinement les mêmes 100 ans d'avance sur la réalisation de la première photographie en couleur, comme le rappelait la plaque de sa maison natale. Son idée était de filtrer la lumière de source de l'objet photographié, avec trois écrans, rouge, vert, bleu, évidemment, de façon à ne retenir dans chacun des trois clichés que la lumière de chaque couleur primaire; ainsi la pellicule était elle impressionnée seulement par les rayons rouges dans la première (les autres étant bloqués par le filtre, etc...). En projetant les trois images, chacune à travers un écran de couleur correspondant, il réussit la synthèse!
Ah, oui, précision: en bon écossais, il avait choisi pour cet essai historique... un ruban de tartan, bien sûr!
C'est inexact, à double titre. En premier lieu, l'histoire a fait justice de l'efficacité de leurs démarches respectives: Fourier a eu raison de se dégager d'un débat enlisé et sclérosant, qu'il n'avait pas les moyens de trancher, pour faire avancer l'étude de la propagation; comme ont eu ensuite raison ceux qui décidèrent de réenvisager la question laissée en suspens: ce fut l'essor de la thermodynamique et de la mécanique statistique. D'autre part, ils étaient tous deux de fervents admirateurs de Fourier et de sa manière: un "poème mathématique" pour Kelvin, et quant à l'avis de Maxwell, en voici l'enthousiasme visionnaire:
Et c'est en 2008 que fut inaugurée sur la principale de ces artères, George Street, un monument par lequel son Écosse natale lui rend hommage. Il aurait été difficile de trouver un emplacement mieux approprié: dans son quartier de naissance, au début de la plus grande rue, dans laquelle se trouve, non loin de là, le bâtiment de la Royal Society of Edinburgh, commanditaire de la statue - il en fut un membre éminent. La rue qui passe dans son dos fait face au grandiose monument néogothique dédié à Walter Scott, emblème de l'Écosse littéraire; Maxwell occupe, dans les sciences physiques et mathématiques, une place analogue. Quand on veut résumer la physique à trois géants, ils se nomment, par ordre chronologique: Newton, Maxwell et Einstein. Or, Maxwell est très exactement celui qui fera basculer la physique de son ancien monde, celui de la perfection newtonnienne, au nouveau monde relativiste incarné par Einstein.
| Vue générale; à l'arrière, St-Andrew square | Maxwell regarde George street... | ... vers le bâtiment de la Royal Society, 500m à gauche. |
La Maison Natale
Le petit James naît le 13 Juin 1831, dans la maison familiale, au n°14, India Street. C'est l'une des rues transversales à George street, en pente sensible, bordées de maisons bourgeoises, certes, mais modestement, et dont chacune ressemble à sa voisine. L'allure générale, renforcée par le gris de la pierre, est plutôt austère.| India street, à l'angle d'Herriott Row |
India street; la maison natale est la première à gauche | India street, le numéro XIV |
Une troisième plaque a été apposée, juste à droite de la sonnette. Son cuivre lui si fort qu'on peine à lire de face, et qu'en inclinant un peu son angle de visée on y voit surtout... les maisons d'en face, inlassablement du même modèle. Fort heureusement, les mathématiques peuvent nous tirer de ce mauvais pas: il suffit d'augmenter encore plus l'angle de visée (donc de déformer beaucoup plus, dans un premier temps!) avant de... redresser l'image grâce à une transformation géométrique matricielle. La chose est gérée intuitivement, à la souris, par de nombreux logiciels de retouche: le Mathouriste a, par exemple, utilisé Gimp, logiciel libre. Et voici le résultat, à droite! Vous n'avez plus qu'à méditer l'avis d'Einstein sur Maxwell...
 |
La James Clerk Maxwell Foundation met à votre disposition sur la toile l'itinéraire d'une promenade illustrée et commentée; le Mathouriste s'est laissé guider... et vous conseille de faire de même.
Jeunesse et Formation
James et ses parents quittent rapidement Édimbourg
pour Glenfair, où il est élevé. Mais il y revient
en 1841 pour ses années de collège, et loge alors chez sa
tante, au 31, Herriott street, à quelques centaines de
mètres seulement et un angle droit près de la rue
où il est né.
Il étudie à l'Edinburgh Academy, qui n'a guère changé d'allure depuis... C'est là qu'il devient l'ami de Peter G. Tait (futur auteur du célèbre traité de physique connu comme LE Thomson &Tait, T&T -Maxwell s'amusait, lui, de les appelerT & T'
) et qu'il écrit son premier article sur un thème de
géométrie, une généralisation des ovales de Descartes.
Car si les exercices très répétitifs de Latin et
de Grec ne suscitent guère son enthousiasme, il se
révèle d'une surprenante habileté dès qu'on
aborde la Géométrie!
Comme il est trop jeune pour le présenter lui même à la, c'est son professeur, James Forbes, qui s'en charge. Tout n'est pas nouveau, certes; d'autres, et non des moindres, ont mentionné ces courbes avant lui... mais n'ont pas étés aussi ingénieux pour les tracer!
Poursuivre à Cambridge s'impose évidemment! Contre l'avis de Forbes, il choisit d'entrer à Peterhouse plutôt qu'à Trinity, histoire de retrouver son ami Tait. Dès leur première matinée, on fait visiter à tous les nouveaux arrivants Trinity College...
Comme il est trop jeune pour le présenter lui même à la, c'est son professeur, James Forbes, qui s'en charge. Tout n'est pas nouveau, certes; d'autres, et non des moindres, ont mentionné ces courbes avant lui... mais n'ont pas étés aussi ingénieux pour les tracer!
|
"Mr
Clerk Maxwell suggère ingénieusement l'extension de la
propriété usuelle des foyers des coniques à des
courbes de degré pkus élevé [...] L'auteur a
conçu des dispositifs mécaniques simples pour les
engendrer, à l'aide d'épingles et de fils s'enroulant
autour. [...]
Les
ovales de Descartes sont étudiéss dans sa
Géométrie, où il a donné un moyen
mécaanique de les décrire, mais seulement dans un
cas particulier, et sa méthode est moins simple que celle de Mr
Maxwell. La démonstration des propriétés optiques
a été donnée par Newton dans les Principia [...], et par Huyghens en 1690, dans son Traité de la Lumière.
On n'avait probablement pas soupçonné jusque là
qu'existât une méthode aussi simple et
élégante pour décrire ces courbes à l'aide
d'un fil et d'épingles [...]."
Sur la Description des Courbes Ovales, et de celles qui ont plusieurs Foyers, avec des remarques du Pr. Forbes
[texte complet] |
Poursuivre à Cambridge s'impose évidemment! Contre l'avis de Forbes, il choisit d'entrer à Peterhouse plutôt qu'à Trinity, histoire de retrouver son ami Tait. Dès leur première matinée, on fait visiter à tous les nouveaux arrivants Trinity College...
Trinity College, Cambridge. À gauche, la chapelle.
Au bout d'un trimestre, il migre à Trinity. On s'y entraîne frénétiquement au célèbre examen, les Mathematical Tripos, qui certes requièrent virtuosité, rapidité et habileté, mais reposent sur un corpus fort peu moderne, dont les Éléments d'Euclide demeurent l'alpha et l'oméga. Maxwell compare l'entraînement à un apprentissage du jonglage et s'en acquitte assez consiencieusement pour être classé deuxième; le major, ou Senior Wrangler comme il est de tradition de l'appeler, est un autre futur grand mathématicien, Edward Routh (surtout connu pour son critère de stabilité des systèmes contrôlés, toujours très utilisé en ingéniérie).
|
"
La tradition mathématique était essentiellement celle
qu'avait institué le grand Isaac Newton, qui avait
été étudiant puis professeur à Cambridge [...]. [Ses]méthodes
étaient plus géométriques qu'algébriques,
et par suite le cursus du Tripos reposait sur l'œuvre d'Euclide,
le fondateur de la géométrie dans l'antiquité
grecque. Si grande était l'aura de Newton que, pendant des
années, les auteurs de sujet ignoraient compètement les
grandes avancées réalisées par les
mathématiciens français, notamment Legendre, Lagrange, Laplace, Cauchy, Monge, Fourier et Poisson, et d'autres comme le suisse Euler
ou le plus grand de tous, l'allemand Gauss. Ils finirent par se rendre
compte de leur retard, et l'avaient rattrapé à
l'époque des études de James, grâce aux efforts
d'un petit groupe incluant Charles Babbage, aujourd'hui considéré comme le père de l'ordinateur."
B. Mahon, The Man who changed Everything: the Life of James Clerk Maxwell (Wiley)
NB: les liens renvoient ici aux pages de notre site où sont honorés ces mathématiciens.
|
Il enseignera ensuite la physique à Aberdeen (plus de détails dans ce texte), à Londres au King's College (1860-65: plus de détails dans ce texte), poste auquel il renoncera pour retourner dans sa chère Écosse, à son domaine de Glenfair. C'est là qu'il donnera naissance, en 5 ans, à la théorie électromagnétique qui va révolutionner la science et les techniques.
Le Monument d'Édimbourg
Au premier coup d'œil, on le daterait volontiers du XIXème siècle, tant il est conforme aux canons de cette époque: reproduction fidèle, pause très académique, évocation de ses principaux travaux, dans sa statue que dans les plaques du socle... pourtant, il a été réalisé au XXIème siècle! Par un artiste qui, non seulement est considéré, mais se revendique lui-même comme un néo-classique: Alexander Stoddart.
| Né en 1959 à Édimbourg, Stoddart
s'est délibérément placé à contre
courant du Pop Art souverain pendant ses années d'étude à la Glasgow School of Art (1976–1980). Voire de façon provocante, essuyant de ce fait des insultes de ses condisciples! Le temps a coulé, il a désormais été très officiellement nommé Her Majesty's Sculptor in Ordinary in Scotland en 2008, et affiche sa volonté de glorifier les héros de sa terre natale, à laquelle il est profondément attaché. C'est ainsi qu'il a doté le Royal Mile d'Édimbourg de statues de l'économiste Adam Smith (devant la cathédrale St-Gilles) et du philosophe David Hume. |
Deux photographies ont visiblement inspiré le sculpteur: dans la première, le grand physicien pose avec, à ses pieds, son terrier favori, Toby -probablement inspiré par une photographie célèbre (quoique d'auteur inconnu). On aime bien les chiens, dans la sculpture écossaise: outre le célèbre Greyfriars Bobby, celui de Walter Scott est représenté aux pieds de son maître!
Dans la seconde, on le voit tenir le disque à tranches colorées qui lui a servi à faire la démonstration de la synthèse de la lumière blanche à partir de ses composantes de couleur (grâce à la permanence rétinienne, l'œil perçoit la somme de toutes les couleurs), opération inverse de l'analyse de cette même lumière, décomposée par Newton dans sa célèbre expérience du prisme. Analyse et synthèse du signal lumineux: nous voici déjà, par l'expérience, en pleine théorie de Fourier, sur laquelle nous verrons Maxwell exprimer son enthousiasme un peu plus loin.
 |
 |
||
| avec son épouse et son chien (1869) | Maxwell, et son disque coloré (Archives Emilio Segrè, AIP) |
Maxwell, le disque et la synthèse | Newton, le prisme et l'analyse |
À l'arrière, deux plaques: une grande indique les nombreuses instituions scientifiques dont Maxwell était membre; sur la petite sont gravées les quatre fameuses équations de l'électromagnétisme, reprises de manière plus visible à l'avant du monument, insérées au milieu des pavés.
La souscription a été lancée en 2006 par la RSE et son président, Sir Michael Atiyah; voir la plaquette des donateurs et un poème inspiré par la statue.
Sous le Disque Coloré... le Triangle!
Puisque ce disque est l'un des
éléments de la statue, il mérite quelques
détails supplémentaires. Comment, direz-vous, une fois de plus, le Mathouriste s'aventure dans la physique? Outre
qu'il n'y a aucun déshonneur à cela, vous verrez que les
mathématiques et... l'informatique y trouveront leur compte!
C'est encore avec James Forbes que Maxwell expérimente la question de la synthèse des couleurs: son professeur est persuadé qu'en proposant "les 7 couleurs de l'arc en ciel" (7 comme 7 degrés en musique, inspiration plus mystique que véritablment scientifique!), Newton propose un système largement redondant. Il croit davantage à l'idée de Thomas Young, émise une bonne cinquantaine d'années auparavant (1802), selon laquelle trois couleurs primaires (rouge, jaune, bleu) suffisent pour produire le blanc et qui, en médecin et physiologiste, postule l'existence sur la rétine de trois différents types de récepteurs. Mais Young est partisan d'une optique ondulatoire (voir notre page Fresnel, où sont évoquées ses célèbres fentes). Crime de lèse-majesté au pays de Newton, où seule son idée d'une lumière corpusculaire a droit de cité! Donc Young est ignoré ou dénigré...
Pourtant, les peintres ne savent-ils pas depuis longtemps qu'ils peuvent "tout faire" avec trois couleurs primaires? Forbes veut le prouver avec un disque rotatif ne portant que les trois couleurs primaires -celui qui est représenté sur la statue, dont la vitesse, alliée au phénomène bien connu de la persistence rétinienne, produira sur l'œil l'impression de blanc.
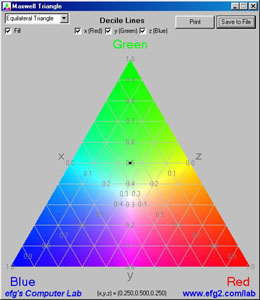
Pour définir mathématiquement la relation d'une couleur quelqconque aux composantes primaies, James eut alors l'idée de ce que l'on appela désormais triangle de Maxwell: chaque couleur est représentée par un point intérieur d'un triangle dont les sommets sont le rouge, le vert et le bleu; très précisément par 3 coordonnées de somme 1, représentant le pourcentage de rouge, de vert, et de bleu. Le lecteur averti d'un peu de géométrie reconnaîtra un système de coordonnées barycentriques: chaque point est centre de gravité des trois sommets, affectés d'une pondération représentant leur importance dans le mélange.
C'est encore avec James Forbes que Maxwell expérimente la question de la synthèse des couleurs: son professeur est persuadé qu'en proposant "les 7 couleurs de l'arc en ciel" (7 comme 7 degrés en musique, inspiration plus mystique que véritablment scientifique!), Newton propose un système largement redondant. Il croit davantage à l'idée de Thomas Young, émise une bonne cinquantaine d'années auparavant (1802), selon laquelle trois couleurs primaires (rouge, jaune, bleu) suffisent pour produire le blanc et qui, en médecin et physiologiste, postule l'existence sur la rétine de trois différents types de récepteurs. Mais Young est partisan d'une optique ondulatoire (voir notre page Fresnel, où sont évoquées ses célèbres fentes). Crime de lèse-majesté au pays de Newton, où seule son idée d'une lumière corpusculaire a droit de cité! Donc Young est ignoré ou dénigré...
Pourtant, les peintres ne savent-ils pas depuis longtemps qu'ils peuvent "tout faire" avec trois couleurs primaires? Forbes veut le prouver avec un disque rotatif ne portant que les trois couleurs primaires -celui qui est représenté sur la statue, dont la vitesse, alliée au phénomène bien connu de la persistence rétinienne, produira sur l'œil l'impression de blanc.
| " Il essaya d'obtenir le blanc par un mélange de rouge, de jaune et de bleu -comme les artistes. Mais aucun mélange ne convenait. Perplexe, il essaya de mélanger seulement deux couleurs, le bleu et le jaune, afin de vérifier que le disque, en tournant, paraîtrait vert. Mais à sa grande surprise, ce qu'il vit n'était pas vert, mais rose pâle. | |
|
C'était
encore plus déroutant, mais James commença à
expérimenter de son côté et trouva bientôt
l'explication. Il y a une différence fondamentale entre un mélange de lumières, en faisant tourner le disque, et un mélange de pigments,
comme on le ferait sur la palette. Les pigments agissent comme des
extracteurs de couleur, de sorte que ce que l'on voit après
mélange est l'ensemble des couleurs du spectre lumineux qui
n'ont pas été absorbées par l'un ou l'autre.
En d'autres termes, mélanger les pigments est un procédé soustractif, alors que mélanger des lumières est additif.
Tout ceci est aujourd'hui une connaissance de base pour les
étudiants en physique, mais c'était uen remise en cause
des bases dans les années 1850. Quand James fit l'essai avec un
disque portant comme couleurs primaires le rouge, le vert et le bleu, cela marcha magnifiquement."
B. Mahon, The Man who changed Everything: the Life of James Clerk Maxwell (Wiley)
|
|
Pour définir mathématiquement la relation d'une couleur quelqconque aux composantes primaies, James eut alors l'idée de ce que l'on appela désormais triangle de Maxwell: chaque couleur est représentée par un point intérieur d'un triangle dont les sommets sont le rouge, le vert et le bleu; très précisément par 3 coordonnées de somme 1, représentant le pourcentage de rouge, de vert, et de bleu. Le lecteur averti d'un peu de géométrie reconnaîtra un système de coordonnées barycentriques: chaque point est centre de gravité des trois sommets, affectés d'une pondération représentant leur importance dans le mélange.
|
|
| le triangle de Maxwell (site:egf's computer lab) |
première mention de cette "forme géométrique" , dans une lettre datée du 4 janvier 1855. Noter que le sytème primaire inclut le violet à la place du bleu. |
La télévision en couleur, puis les moniteurs d'ordinateur, ont
repris ce principe: c'est pourquoi vous branchez parfois des câbles RGB
(Red, Green, Blue...). Le
blanc "parfait" est le centre de gravité du triangle, et, en joignant
chaque sommet à ce point, puis en prolongeant jusqu'au pied de la
médiane sur le côté opposé, on obtient la couleur "opposée" à la
couleur primaire du sommet. Voilà pourquoi, lorsque vous utilisez un
logiciel de retouche d'image pour corriger les couleurs d'une photo -ce
qui n'a rien d'infâmant, car les capteurs de l'appareil n'ont pas les
mêmes réctions que celles de l'œil!- vous disposez de trois curseurs:
|
Puisque les pigments se composent par soustraction, vous ne serez plus surpris de voir, dans votre imprimante, trois cartouches des couleurs opposées aux couleurs de synthèse additive de l'écran: cyan, jaune et magenta!
Une démonstration des deux synthèses est proposée dans cette page, où les curseurs de l'image reproduite ci-dessous sont mobiles à la souris, et le résultat immédiatement visible, histoire de vérifier que vous avez bien tout compris.
Maxwell ne pouvait deviner, avec plus de 100 ans d'avance, ce succès universel de son triangle... ainsi en va-t-il des travaux des grands précurseurs! Il assula en revanche pleinement les mêmes 100 ans d'avance sur la réalisation de la première photographie en couleur, comme le rappelait la plaque de sa maison natale. Son idée était de filtrer la lumière de source de l'objet photographié, avec trois écrans, rouge, vert, bleu, évidemment, de façon à ne retenir dans chacun des trois clichés que la lumière de chaque couleur primaire; ainsi la pellicule était elle impressionnée seulement par les rayons rouges dans la première (les autres étant bloqués par le filtre, etc...). En projetant les trois images, chacune à travers un écran de couleur correspondant, il réussit la synthèse!
Ah, oui, précision: en bon écossais, il avait choisi pour cet essai historique... un ruban de tartan, bien sûr!
 |
 |
| Les trois clichés d'origine sont conservés dans sa maison natale. (source de l'image) | |
"Et Dieu dit..."
Simplicité et postérité pourraient être les deux mamelles de la beauté en sciences: à ce titre, les équations de Maxwell méritent indiscutablement leur place au Hall of Fame, et Ian Stewart ne s'y est pas trompé, qui les a incluses parmi ses 17 équations qui ont changé le monde.Témoignage
a posteriori de leur succès, elles ont inondé les
T-shirts des étudiants de physique. Oui, loin devant le E=mc² d'Einstein ou la formule de l'attraction universelle de Newton:
Mais dites vous bien que les mathématiques sont comme la sculpture: il faut beaucoup de travail pour faire sortir la beauté et la simplicité du matériau brut. Newton avait trouvé sa lumineuse formule "en y pensant toujours" disait-il lui-même -la célèbre pomme n'étant que le déclencheur; et avec une référence malicieuse, Einstein répondait quant à sa propre découverte: "en y pensant souvent". On ne s'étonnera donc pas que Maxwell ait dépensé beaucoup de temps, d'encre et de sueur avant que la postérité ne retienne que 4 lignes...
< Cette histoire,on vous la racontera prochainement, dans cette page: suivez le lien!>Mais dites vous bien que les mathématiques sont comme la sculpture: il faut beaucoup de travail pour faire sortir la beauté et la simplicité du matériau brut. Newton avait trouvé sa lumineuse formule "en y pensant toujours" disait-il lui-même -la célèbre pomme n'étant que le déclencheur; et avec une référence malicieuse, Einstein répondait quant à sa propre découverte: "en y pensant souvent". On ne s'étonnera donc pas que Maxwell ait dépensé beaucoup de temps, d'encre et de sueur avant que la postérité ne retienne que 4 lignes...
Maxwell et Fourier
On a parfois dit que, revenant à la recherche des causes mécaniques de la chaleur (le mouvement des molécules), Kelvin et Maxwell s'opposaient à Fourier, qui "refusait" de s'y intéresser; qu'on se souvienne du célèbre début de sa préface (voir notre page sur son traitement de la chaleur):| "Les causes primordiales ne nous sont point connues; mais elles sont assujetties à des lois simples et constantes, que l'on peut découvrir par l'observation [...].La chaleur pénètre, comme la gravité, toutes les substances de l'univers, ses rayons occupent toutes les parties de l'espace. Le but de notre ouvrage est d'exposer les lois mathématiques que suit cet élément." |
C'est inexact, à double titre. En premier lieu, l'histoire a fait justice de l'efficacité de leurs démarches respectives: Fourier a eu raison de se dégager d'un débat enlisé et sclérosant, qu'il n'avait pas les moyens de trancher, pour faire avancer l'étude de la propagation; comme ont eu ensuite raison ceux qui décidèrent de réenvisager la question laissée en suspens: ce fut l'essor de la thermodynamique et de la mécanique statistique. D'autre part, ils étaient tous deux de fervents admirateurs de Fourier et de sa manière: un "poème mathématique" pour Kelvin, et quant à l'avis de Maxwell, en voici l'enthousiasme visionnaire:
 |
Références
- Site de la James Clerk Maxwell Foundation: images, textes... une mine d'informations!
- Les Cahiers de Science et Vie: Maxwell ou les champs de la lumière (Hors série n° 17, octobre 1993)
- Les Génies de la Science (Pour la Science): Maxwell: Champ, particules, couleurs (Hors série n° 24, août 2005)
- L. CAMPBELL, The Life of James Clerk Maxwell, with a selection of his Correspondance and Occasional Writings (Macmillan)
- B. MAHON, The Man who changed Everything: the Life of James Clerk Maxwell (Wiley)
- I. STEWART, 17 équations qui ont changé le monde (Champs-Sciences)
< la suite, prochainement, dans cet espace!>
Revenir
à la Home
Page du
Mathouriste