Omar KHAYYAM
du Septième Ciel au Troisième Degré ...
"Omar Khayyam était
un homme qui regardait le ciel en face. Il aimait les astres, leurs
mouvements; il aimait à calculer leurs apparitions , leurs
influences, leurs éclipses. C'était un astronome et un
mathématicien. Mais pas seulement.
À force de sonder le ciel, il avait mesuré la durée dérisoire des
hommes face à leurs étoiles, le néant auquel ils sont voués. Et ce
chiffre secret, ce point zéro où apparaît et s'abîme tout ce qui vit,
l'a fait poète."
Chouchana Bourhobza, Postface aux Quatrains (Éd. Mille et Une Nuits)
Sa place dans nos pages,
il la doit évidemment à ses talents de mathématicien (et d'astronome),
mais on ne peut -ni ne veut ici- le dissocier du poète et philosophe
qu'il fut aussi. Et ne vous sera-t-il pas agréable, face à chacun des
cas du magistral Traité sur les Équations du Troisième Degré, de lire un de ses non moins célèbres Rubáiyáts ? C'est ce à quoi le Mathouriste vous convie!
|
|
Poète et Mathématicien! Est-ce bien raisonnable? Est-ce seulement possible?
En voilà une question saugrenue!
Mais, hélas, témoignage accablant du cloisonnement des disciplines,
maladie endémique du système scolaire... voire universitaire.
Commençons, à titre de mise en bouche, par un quatrain typique de
Khayyam, et qui n'a rien à voir avec ses activités scientifiques: il
n'y est question que d'un moment épicurien, du plaisir dans un
jardin... délicatement souligné dans cet exemplaire par une peinture du miniaturiste Hossein Behzad (1894 – 1968),
comme tous les autres poèmes du recueil. Celui-ci, quadrilingue, permet
d'apprécier la calligraphie et la disposition traditionnelle persanne
des quatre vers, ainsi que la traduction princeps (1859) de l'anglais Edward FitzGerald qui fit connaître l'œuvre en Europe; la traduction française est de l'iranologue Gilbert Lazar. Le Mathouriste en a fait acquisition à Isfahan (Merci à Gérard, grand connaisseur du pays, pour ses précieux conseils).
 édité par Behzad Publications, (2005)
édité par Behzad Publications, (2005)
"Finalement,
après avoir fait le tour de toutes ces possibilités, le plus simple est
bien de penser que Shakespeare a réellement existé."
Un exemple contemporain fera réfléchir: celui de... Fourier! Aux XXème et XXIème siècles, bien peu nombreux encore sont les mathématiciens ou les physiciens qui savent qu'il a préfacé cet ompilé la Description de l'Égypte,
encouragé et protégé le jeune Champollion; et pour ainsi dire il n'est
pas un égyptologue qui se doute que le talentueux préfet, préfacier de
la Description, a édifié une théorie mathématique qui profite à sa discipline quand elle recourt à l'imagerie (scanner, RMN) ou à la spectroscopie infra-rouge! Deux siècles seulement nous séparent de lui... Alors, quand cela remonte, pour le cas de Khayyam, au XIème siècle !!!
Aussi adopterons nous sans réticence l'idée du poète
mathématicien. Ce qui nous amène à une précision importante: les
quatrains sont, certes, écrits avec l'alphabet arabe, mais ils sont
écits dans la langue persanne. Si la conquête arabe a imposé une
religion et une graphie, l'identité persanne est restée très forte au
cours des siècles, et les habitants de cette terre ont conservé
farouchement leur langue, leur histoire et leurs coutumes jusqu'à
aujourd'hui... et ils en on vu passer, des envahisseurs! Mais...
si Khayyam écrit ses poèmes en Persan, il rédige ses écrits mathématiques en arabe,
pour en assurer la meilleure diffusion dans le monde musulman.
L'Arabe est en effet la langue de la science de tout le temps de la
splendeur des empires musulmas (en gros, du IXème au XVème siècle) , comme le seront, en Europe, le latin aux XVIème et XVIIème siècles, le Français aux XVIIIème et XIXème siècles... et l'Anglais -enfin, l'Américain dans le monde à partir du XXème siècle,
n'en déplaise aux quelques ministres qui, complètement étrangers à la
réalité du monde de la recherche, ont tenté en vain d'imposer le
Français pour les colloques tenus en France... trop tard! Le besoin
d'une langue de circulation commune et pratique n'a donc rien de neuf,
ni d'extraordinaire; il nous semblait utile de rappeler cette
considération simplement pragmatique.
Mais revenons aux quatrains de Khayyam: tous n'ont
pas la même insouciance légère que le précédent. Beaucoup mêlent à
l'épicurisme la vanité de l'existence et l'angoisse de la mort. Dans
celui-ci, c'est la noirceur qui domine:
 même édition
même édition
La vie bien peu connue d'un Polymathe
Ce que nous savons de lui est fait de bien peu de certitudes
historiques et d'une part certaine de légendes, ou, tout au moins,
d'histoire romancée. Si cette dernière ne pose pas de problème
lorsqu'elle est clairement assumée -avec le talent d'Amin Maalouf dans
son roman Samarcande, ce qui est dit de lui ici ou là parait bien
peu fiable. Nous évoquerons ici trois lieux où sa présence est
attestée, associés à quelques moments de sa vie. Et un autre, mais
n'est-ce qu'un roman?
Nishapur
Omar Khayyam est né le 18 mai 1048 dans
cette ville de la province du Khorassan; son nom laisse penser qu'il
était le fils d'un marchand de toiles de tentes.
Omar Khayyam est né le 18 mai 1048 dans
cette ville de la province du Khorassan; son nom laisse penser qu'il
était le fils d'un marchand de toiles de tentes. On peut trouver ce nom de famille dans le Khorassan,
comme le prouve l'enseigne ci-contre: passé l'étonnement de la
découverte, on se dit qu'il y a tout de même fort peu de chance que
cette raison sociale soit un hommage-souvenir .
|

|
| boutique à Mashhad, dans le Khorassan (Iran) |
| À' Nishapur, l'enfant du pays est
si vénéré qu'il a fallu placer sous pexiglass son buste, pour qu'il ne
soit pas dégradé par le contact des mains de tous ceux qui viennent lui
rendre hommage! |

|

|

|
Nishapur (Iran), dans le parc, près de son mausolée
|

|
De sa formation, on ne sait que peu de choses. Le quatrain ci-contre ne
nous renseigne pas, et le genre ne se prête pas à une citation
explicite. Mais le bibliographe Al-Safadi le présente comme disciple de
Bahmaniar, élève d'Ibn Sinna (plus connu en Europe sous le nom d'Avicenne ). Bahmaniar semble avoir été instruit par son maître en logique, physique et philosophie (notre page
vous rappelle qu'Avicenne a pratiqué à égalité les sciences et les
lettres); on peut supposer que sa transmission fut aussi éclectique.
Rien d'explicite ne concerne les mathématiques, mais les écrits de
Khayyam prouvent, en les citant nommément, qu'il a bien étudié les
livres de ses prédécésseurs les plus importants: Al-Mahani, Al-Khazin,
Abu-al-Wafa, Ibn Al-Haytham... .
|

|
|
|
Il a terminé ses jours dans cette même ville, le 4 décembre 1131 ; il s'y était retiré depuis plusieurs années.
Un autre de ses contemporains, l'écrivain Nizami Aruzi, raconte: «
J'avais rencontré Omar Khayyam vingt ans avant sa mort, dans la ville
de Balkh [...]
et vu sa renommée, je le suivais comme son ombre pour recueillir
chacune de ses paroles. C'est ainsi que je l'ai entendu
dire: "Ma tombe sera en un lieu tel qu'à chaque printemps,
le vent du nord y répendra des fleurs" [...] Je suis passé par Nishapur quatre ans après la mort de Khayyam. Comme
j'éprouvais envers lui la vénération que l'on doit à un maître de la
science, je me suis rendu en pélerinage à sa dernière demeure. Un guide
me consuisit au cimetière. En tournant à gauche après l'entrée, j'ai vu
la tombe adossée au mur du jardin.Des poiriers et des pêchers
étendaient leurs branches qui avaient répandu leurs fleurs sur la
sépulture, si bien quelle était cachée sous un tapis de pétales. »
Amin Maalouf, Samarcande.
| 
|
ci-contre : Sur la tombe d'Omar Khayyam, par Jay Hambidge (source: WikimediaCommons)
|
Le
mausolée actuel, qui attire toujours beaucoup de monde, est... un peu
plus moderne! Il a été édifié en 1963, conçu par l'architecte iranien Houshang Seyhoun (1920 – 2014) , formé à l'École nationale supérieure des Beaux-Arts
de Paris, puis en architecture à l'Université de Téhéran. Il a été
influencé par l'architecture en béton développée en Europe dans cette
large moitié du XXème siècle, qualifiée de brutaliste pour son utilisation du matériau à l'état brut. Alors qu'il avait appliqué strictement ce principe, en 1952,
sur le mausolée d'Avicenne à Hamadan (en dépit de la référence à une
forme traditionnelle, l'impression était, pour le coup, assez...
brutale), il l'a ici adouci par les décors de faïence aux couleurs
classiques du pays -d'autant que Nishapur a longtemps prospéré sur
l'extraction et le commerce des turquoises. Les textes qui y
apparaissent sont quelques Rubáiyáts... mais ne comptez pas sur le Mathouriste pour vous dire lesquels!
|
 |

|

|
En son centre, le tombeau, très simple, est de forme polyédrale. Et
chaque Iranien qui vient ici tient à se faire photographier avec le
célébrissime poète!
|

|

|

|
Nishapur (Iran), le tombeau dans le mausolée
|
Il n'est donc pas étonnant de le retrouver sur un timbre
commémoratif (paru en 2018) . Plus insolite, plus amusante, cette
lampe, dans une boutique de Mashhad.
Samarcande
Omar Khayyam y aurait séjourné de 1072 à 1074,
avant de partir pour Ispahan. Difficile à vérifier,mais, légende ou
réalité, c'est le point de départ choisi par Amin Maalouf pour son
passionnant roman. Le Mathouriste tient
à réaffirmer ici, haut et fort, son soutien à tout écrivain qui, par
ailleurs bien documenté, comble les vides de l'histoire au gré de son
imagination: c'est de ce droit, bien appliqué, que naîtra le plaisir du
lecteur! Preuve par l'exemple:
" [...]Abou
Taher respire, profondément, et intime à ses hommes un ordre sec. Ils
s'éloignent. Dès qu'ils ont refermé la porte, il se dirige vers un coin
du divan,
soulève un pan de la tapisserie, puis le couvercle d'un coffret en bois
damassé. Il en retire un livre qu'il offre à Omar d'un geste
cérémonieux. [...]
Un cuir épais, rêche, des renfoncements en queue de paon, des bords de feuille irréguliers, effrités. Mais lorsque Khayyam l'ouvre, en cette inoubliable nuit d'été, il ne contemple que deux cent cinquante six pages vierges, ni poèmes encore, ni peintures, ni commentaires en marge, ni enluminures.
Pour masquer son émotion, Abou Taher prend un ton camelot:
«C'est du kaghez
chinois, le meilleur papier qui ait jamais été produit par les ateliers
de Samarcande. Un juif du quartier de Maturid l'a fabriqué à mon
intention, selon une antique recette, entièrement à vbase de mûrier
blanc. [...]
Sa voix trébuche, se relève essouflée:
- Garde ce livre. Chaque fois qu'un
vers prendra forme dans ton esprit, qu'il s'approchera de tes lèvres,
cherchant à sortir, refoule-le sans ménagement, écris-le plutôt sur ces
feuilles qui resteront au secret. Et en écrivant, pense à Abou Taher. » "
Amin Maalouf, Samarcande.
|
Cette première apparition du Manuscrit de Samarcande -celui des Rubáiyáts,
bien sûr, sort de l'imagination du romancier, de même que le destin qu'il lui
réserve: non, nous ne spoilons pas, c'est la première phrase du roman:
"Au fond de l'Atlantique, il y a un livre. C'est son histoire que je vais vous raconter.
Peut-être en connaissez vous le dénouement [...] :
lorsque le Titanic
a sombré, dans la nuit du 14 au 15 avril 1912, au large de Terre-Neuve,
la plus prestigieuse des victimes était un livre, exemplaire unique des
Rubayats d'Omar Khayyam, sage persan, poète, astronome."
Amin Maalouf, Samarcande.
|
Samarcande n'est pas encore la magnifique cité que nous visitons et admirons aujourd'hui: la place du Reghistan n'est qu'un marché bruyant, et ses splendides medersas ne seront édifiées qu'à partir du XVème siècle
-la première par le prince astronome Ulugh Beg. Entretemps, Genhis Khan
l'a ravagée, puis Tamerlan l'a bien malmenée, avant de la reconstruire
pour en faire sa capitale. Mais c'est bien là que fut bâtie la première usine de pâte à papier du monde islamique, après que des artisans chinois aient été capturés lors de la bataille de Talas (751) où s'affrontèrent lIslam et la Chine.
Quant au grand cadi Abou-Taher, c'est un personnage réel, protecteur de Khayyam, à qui celui-ci dédie cet autre manuscrit qui va occuper la suite de nos pages:
"Lorsque Dieu Très
Haut m'a accordé la grâce de m'attacher à notre très illustre et unique
Seigneur, Juge des Juges, l'Imam, le Seigneur Abu Tahir -que Dieu
perpétue son éminence et confonde ceux qui le jalousent, ainsi que ses
ennemis- j'avais pour lors désespéré de rencontrer un homme possédant aussi parfaitement chaque vertu pratique et théorique:
il joint à la pénétration dans les sciences la fermeté dans les actions
et dans la recherche du bien pour chacun de ses semblables; sa
rencontre m'a comblé le cœur, sa société a rehaussé ma renommée, ma
cause a grandi en puisant à ses lumières, et ma force s'est accrue par
sa munificence et ses bienfaits. Il ne me restait donc plus qu'à suivre
la voie sur laquelle je ne manquerais plus ce que les incertitudes du
temps m'ont fait perdre: présenter ce que je connais certainement des notions scientifiques essentielles, pour approcher son siège altier. C'est
ainsi que j'ai commencé par énumérer ces espèces de lemmes algébriques,
étant donné que les mathématiques méritent d'être les premières."
Omar Khayyam, Traité d'Algèbre et d'Al-Muqabala.
|
" - Alors, te voilà ami du khan, lance Abou Taher dès qu'ils ont quitté le palais. [...] Ne méprise pas la porte qui s'ouvre, ta carrière me paraît tracée à la Cour!
- La vie de cour n'est pas pour moi; mon rêve, ma seule ambition est
d'avoir un jour un observatoire, avec un jardin de roses, et de
contempler éperdument le ciel, une coupe à la main, une belle femme à
mes côtés.
- Belle comme cette poétesse? ricane Abou Taher.
Omar n'a plus qu'elle à l'esprit, mais il se tait. Il craint que le moindre mot échappé ne le trahisse."
Amin Maalouf, Samarcande.
| 
|

|
ci-contre, illustration de Dulac pour les Rubáiyáts
|
ci-dessus, illustration de Sullivan pour les Rubáiyáts
|
"[...]
- Et soudain, dans l'obscurité de cette nuit, dans ce pavillon irréel, dans cette ville irréelle, te voici, femme, belle, poétesse de surcroît, offerte.
Elle rit.
- Offerte, qu'en sais tu? Tu ne m'as pas frôlée, tu ne m'as pas vue, et
ne me verra sans doute pas, puisque je partirai biena vant que le
soleil ne me chasse.
Dans l'obscurité toujours épaisse, un long frottement désordonné de
soie, un parfum. Omar retient son souffle, sa peau est en éveil; il ne
peut s'empêcher de demander, avec la naïveté d'un écolier:
- As tu encore ton voile?
- Je n'ai plus d'autre voile que la nuit."
Amin Maalouf, Samarcande.
|
Ce rêve, Omar va le réaliser grâce à deux autres personnages historiques: le sultan Malik Shah Ier (1055-1092) et son puissant vizir, Nizam-al-Mulk (1018-1092)
"La
délégation de Samarcande au complet s'est prosternée aux pieds de
Malikshah, qui en prend acte d'un hochement condescendant, puis un
certain nombre de notabilités s'est détaché pour se diriger vers Nizam.
Le vizir est impassible [...]
Douze personnes de la délégation de Samarcande ont onbtenu ainsi le privilège de serrer la main qui tient le gouvernail de l'empire. Omar a emboîté le pas au cadi, Abou
Taher a balbutié une formule. Nizam hoche la tête, retient la main dans
la sienne quelques secondes, le cadi en est honoré. Quand vient le tour
d'Omar, le vizir se penche à son oreille et murmure:
- L'année prochaien, comme ce jour, sois à Ispahan, nous parlerons."
Amin Maalouf, Samarcande.
|
Isfahan
C'est l'une des rares certitudes historiques sur la vie d'Omar Khayyam et nous la devons à l'historien Ibn al-Athîr dans son Histoire Complète (Al-Kāmil fī At-tārīkh), composée au début du XIIIème siècle;
il signale sa présence dans la ville en 1074-75, parmi les experts
réunis par le sultan Malikshah pour une importante réforme du
calendrier: il s'agissait de recaler le début d'année (Noruz) sur
l'équinoxe de printemps, selon la tradition persanne millénaire, que
l'Islam n'a pu effacer. Quant au glissement progressif, il était dû à
l'absence de prise en compte de la perte d'un jour (environ) tous les
quatreans, qui a conduit à l'instauration d'année bissextiles.
"Au cours de cette année, Nizam-al-Mulk et le sultan Malikshah ont réuni un groupe de dignitaires des astronomes, et ont fixé le Noruz
le premier point du Bélier , alors que le Noruz avant cela était lors
de l'occupation du milieu du Poisson par le soleil. Ce qu'a fait le
Sultan est devenu le principe des calendriers, et en cette année, on a
fait des observations pour le sultan Malikshah; un groupe de dignitaires des astronomes se sont réunis pour les faire, parmi lesquels Omar ibn Ibrahim al Khayyami [...]. Le Sultan a prodigué énormément d'argent; l'observation a continué jusqu'à sa mort en 485 [1092], et s'est arrêtée après sa mort."
Ibn al-Athîr, Histoire Complète.
|
|
 |
ci-contre: timbre évoquant Khayyam astronome (à voir sur le site de Jeff Miller)
|
| On crédite Khayyam de la proposition d'un cycle de 33 ans contenant 8 années bissextiles ce qui portait la
durée moyenne de l’année à 365,2424 jours, précision supérieure à
celle du calendrier grégorien. (voir la page Wikipedia sur le calendrier solaire persan)
|
Ispahan n'est pas vraiment, à cette époque, "la moitié du Monde", comme s'en vantent encore aujourd'hui les Persans; sa somptueuse place centrale ne sera construite par Chah Abbas Ier qu'au début du XVIIème siècle.
Mais il en émane déjà ce mélange unique de beauté et de nonchalence qiui inspira à Duke Ellington un tableau de sa Far East Suite.
Et qui mieux pour le célébrer que la plus suave sonorité de sax alto
jamais entendue, celle de son cher Johnny Hodges? Il lui tient même la
partition dans cet Isfahan d'anthologie!
De l'observatoire, hélas, plus de traces... mais la Mosquée Jameh
(du Vendredi), dont la construction est contemporaine de la présence en
ville du mathématicien-poète, porte quasi-sûrement la marque d'Omar,
comme on va le voir. Elle se trouve non loin de Meydân-e Kohne, l'ancienne place centrale (ainsi désignée pour la différencier de celle de Shah Abbas), tracée par Malikshah, en instituant sa capitale dans cette ville.
Quoique de dimensions moindres que celle de Shah Abbas (qui, bien
sûr, tenait à montrer s'affirmer comme le plus grand de tous les temps
en prenant le record de dimensions), elle témoigne de ce qui était déjà
la splendeur de la ville au temps d'Omar Khayyam. Après avoir longtemps
souffert de cet abandon, elle a récemment retrouvé un reflet de son
éclat passé, qui permet au visiteur d'aujourd'hui de s'en faire une
idée. Tout juste reprochera-t-il que cela sent un peu trop le neuf, en
méditant sur les conditions de sécurité du chantier de restauration...
comment dire, quelque peu différentes des normes européennes!
Mais revenons à la mosquée, judicieusement inscrite au Patrimoine Mondial de l'Humanité par l'UNESCO (premier édifice islamique ayant adapté la configuration des palais sassanides avec une cour à quatre iwans),
pour y chercher la patte géométrique de notre héros. Ce n'est pas
simple, car elle a été maintes fois malmenée, pillée, incendiée,
reconstruite, aggrandie... -le dernier sévice en date a pour
responsable un missile irakien, lors de la guerre entre les deux pays.
En dépit de cette histoire mouvementée, elle a conservé ce qui en fait
le prototype de toutes les mosquées d'Asie Centrale, sa structure
à quatre iwans placés aux
points cardinaux, encadrant une vaste cour, et deux dômes d'origine
(qualifiés d'exceptionnels par l'UNESCO), l'un au sud -dit de
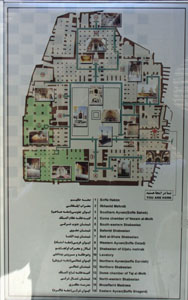
Nizam-al-Molk (1086-87), l'autre au nord -dit de Taj-al-Molk (1088), Le plan affiché à l'entrée aidera à s'y retrouver:
C'est la décoration de l'iwan Ouest qui attirera en premier notre
attention. On y lit en effet l'une des nombreuses démosntrations par
découpage du théorème de Pythagore, celle d'Abu-al-Wafa (940-998)

|

|

|
l'iwan ouest
|
Mosquée du Vendredi: dans l'iwan ouest ... avec Pythagore et Abu-al-Wafa
|
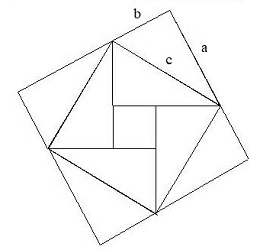
calculant la surrface de deux façons:
( a + b )² = ( a - b )² + 8. (½ ab )
= c² + 4. (½ ab )
soit a² + b² = c²
|
Khayyam a-t-il suggéré ce motif ? L'hypothèse a été avancée, mais il y a plusieurs objections.
D'abord, la décoration de l'iwan est datée du XVIIème siècle.
Certes, mais, pour ce motif en tout cas, ce pourrait être une
restauration d'un motif antérieur, d'autant qu'il est d'un style bien
plus sobre que celui de l'époque séfévide.
D'autre part, à supposer qu'il y en ait eu une version dès la
construction, les artisans avaient-ils besoin qu'un mathématicien
vienne le leur souffler? Ils pouvaient "boire à la source" ce motif,
car Abu -al-Wafa avait écrit un petit manuel pratique à l'usage des artisans, très largement diffusé:
Kitab al-Handasa (Sur l'indispensable aux artisans en fait de construction)
et contenant cette figure didactique.
|
 |
|
Mosquée du Vendredi, à l'intérieur
|
L'esthétique de ces quatre "amandes" (kites pour les anglo-saxons... les amateurs de kitesurf comprendront en observant la forme de leur voile) est peut-être,
c'est une autre hypothèse formulée dans cet article, à l'origine d'une
demande des artisans à Khayyam.
Beaucoup de leurs œuvres s'appuyaient sur des tracés préalables
d'entrelacs de droites et de cercles. Ils auraient souhaité retrouver
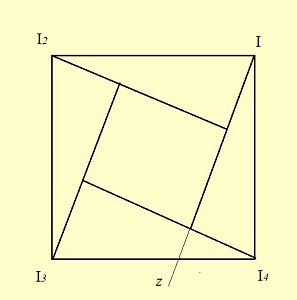
un petit carré central incliné et quatre kites à partir de droites issues des sommets du grand carré. Menons d'un sommet I une demi-droite arbitraire Iz, sans
nous soucier pour l'instant de l'angle qu'elle fait avec le côté du
grand carré; par trois rotations succesives de 90°, on engendre une
figure du type souhaité... à ceci près que les kites sont généralement disgrâcieuses. parce que les longueurs GM et MB sont différentes.
Peut on avoir GM = MB ?
| 
|
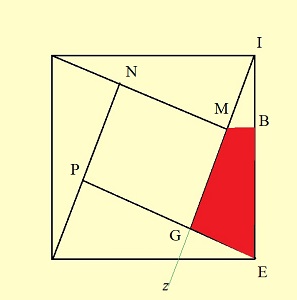 |
Un lecteur d'aujourd'hui peut répondre oui, presque instantanément.
Considérons les deux situations limites, celle où l'angle est nul: le
"petit" carré est confondu avec le grand, et celle où l'angle vaut 45°:
le petit carré est réduit à un point, GM = 0 . Déplaçons doucement , en pensée, Iz de la première position vers la seconde: on voit décroître GM, et croître MB... il doit exister une position où leurs valeurs s'égalent!
Cette intuition peut faire l'objet d'une mise en forme rigoureuse à l'aide du théorème de la valeur intermédiaire, pour qui le connaît. Mais c'est très anachronique! Voici le début de solution qu'a pu proposer Khayyam pour y parvenir et qui expliquerait le très mystérieux point de départ du Traité de la Division du Quart de Cercle.
|
|
|
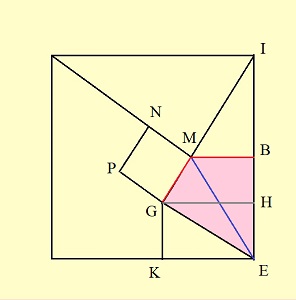
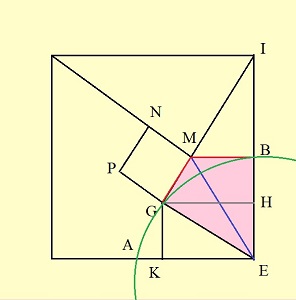
On raisonne par Analyse et Synthèse.
Analyse ("Supposone le problème résolu", disait-on autrefois) :
Si GM = MB , les triangles rectangles EGM et EBM sont égaux (hypothénuse commune et un côté égal) , donc GE = BE = AE en reportant BE sur le côté EK tdu carré; ce qui place les poinst B, G, A sur un même (quart de) cercle de centre E, celui que va étudier Khayyam.
N.B. : les notations peuvent sembler un peu disparates, mais nous
avons voulu conserver celles qui correspondent au texte de Khayyam: :
A, K, E, B, H, I, et nous les avons complétées par L, M, N, P.
|
|
|
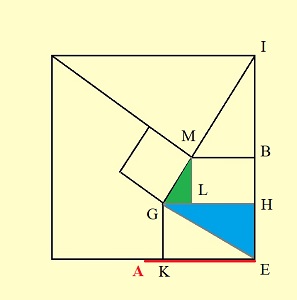 |
On projette orthogonalement G en H sur IE, M en L sur GH.
GM = MB = GK par symétrie de la figure.
Les triangles GHE et MLG sont semblables (égalité des angles à côtés perpendiculaires).On a donc:
C'est (en gras) l'égalité qu'annonce vouloir réaliser Khayyam à la première phrase de son Traité de la Division du Quart de Cercle sans autre commentaire.
|
|
Synthèse : G est défini comme réalisant la division du quart de cercle: 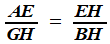 ; M comme intersection de
GI et de la perpendiculaire à IE issue de B. ; M comme intersection de
GI et de la perpendiculaire à IE issue de B.
Retrouve-t-on
GM = MB = GK ?
On
reprend d'une part la similitude des triangles rectangles, toujours
vraie, et d'autre part l'égalité d2 à 2 des côtés du rectangle GHEK.
Ainsi , 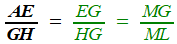 d'une part, et d'une part, et 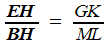 d'autre part. d'autre part.
De l'égalité des termes en gras se déduit 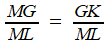 , d'où GM = GK ( = MB par symétrie). , d'où GM = GK ( = MB par symétrie).
Résoudre le problème de l'artisan équivaut donc à réaliser la division du quart de cercle.
|
|
Dans son traité, Omar transforme à nouveau le problème de la
division du quart de cercle en un autre problème équivalent; nous
résumons ici les résultats que l'on établira dans l'épisode II:
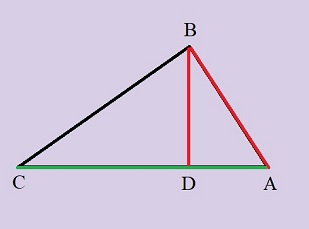
Problème : le Triangle de Khayyam
Construire un triangle ABC rectangle en B, tel que, si l'on abaisse la hauteur BD relative au côté AC , on ait:
AB + BD = AC
Résoudre ce problème équivaut à réaliser la division du quart de cercle; ci-dessus c'est EGI le triangle de Khayyam.
Traduction algébrique :
posant AD = 10 (ce choix est arbitraire, mais il faut fixer une longueur de référence), et prenant BD = x pour inconnue, cela se traduit par
x3 + 200 x = 20 x2 + 2000
Généraliser ?
Ce
problème vient s'ajouter à une collection disparate de questions, pour
certaines connues depuis l'antiquité (duplication du cube en Grèce,
partition de la sphère dans un rapport donné par Archimède), pour
d'autres soulevées par ses prédécesseurs dans la science musulmane
(Ibn-al-Haytham, contruction de l'ennéagone par Al-Biruni) dont le
point commun est de tous se ramener à des équations du troisième degré:
arrive un moment où une étude générale s'impose, et c'est Khayyam qui
l'entreprendra... patience, ce sera notre épisode III !
| 
|
Le triangle de Khayyam serait
aussi, et surtout, selon le
chercheur turc Alpay Ṏzdural, la clef des belles proportions du dôme
nord de la mosquée. Commençons par y jeter un coup d'œil, avant de
savourer celui d'un expert... après quoi, nous pourrons nous intéresser
au secret algébrique des choses; que diable, et ce n'est pas Omar qui
nous contredira, il en va de la géométrie comme du vin: déguster
d'abord, théoriser ensuite!
La salle est carrée au sol; la transition avec le dôme à base
circulaire est assurée, classiquement, par un octogone : quatre
pendantifs s'appuient, chacun sur deux murs à angle droit pour, en
quelque sorte, "couper les coins" du carré. La recette n'a rien
d'extraordinaire en soi: c'est la même que sous le dôme sud; ce qui
change, c'est l'élégance des proportions.

|
 |

|
Isfahan
(Iran): dans la Mosquée du Vendredi, sous le dôme Nord
|
Robert Byron, esthète et grand voyageur, réalise en 1933 un périple en Asie
Centrale -de Venise à Kaboul- dont il tirera un récit demeuré fameux.
Nul ne décrit mieux que lui la différence entre les deux salles sous
dômes:
"La beauté d'Ispahan s'insinue en vous presque à votre corps défendant. Vous roulez à l'aventure [...]
le long de dômes bleu turquoise et jaune printanier qui s'élancent dans le bleu violet d'un ciel limpide.
Vous suivez la rivière semée de fantasques bancs de sable, piégeant ce
bleu dans son argent boueux, bordée de bosquets où la sève crie. [...]
Vous
avez, qui vous regardent, des montagnes mauves, le Luh-é-Soufi avec sa
bosse de Polichinelle, et plus loin encore d'autres massifs se retirant
en une longue suite de vagues couronnées de neige. Et avant même que
vous n'en ayez pris conscience, Ispahan s'est fait indélébile, a
silencieusement glissé dans cette galerie des lieux à qui chacun voue
un culte secret." |

|
[ci-contre, le dôme sud de la Mosquée du Vendredi
voir ses piliers de soutien ci-dessous ]
|
 |
 |
"Je n'ai en rien contribué à cela. Les
monuments m'ont trop occupé.
On pourrait passer des mois en exploration sans être jamais au bout de ses découvertes. Depuis le XIème
siècle, architectes et artisans ont consigné les fortunes de la ville,
ses changements de goûts, de gouvernements, de croyances. Les édifices
sont le reflet de ces péripéties: c'est ce qui fait leur charme, et
celui de beaucoup de vieilles cités. Mais rares sont ceux qui
atteignent, intrinsèquement, au comble de l'art, et placent Ispahan
parmi ces lieux d'exception, tels Athènes et Rome, où vient se délasser
l'humanité entière.""
Robert Byron, Route d'Oxiane.
|
"Les
deux salles à coupoles de la mosquée du Vendredi illustrent de manière
exemplaire ce clivage essentiel. Elles ont toutes deux été construites
sensiblement à la même époque, soit à la fin du XIème siècle;
Dans la plus grande, qui est le sanctuaire principal de la mosquée,
douze colonnes massives engagent une lutte prométhéenne avec le poids
du dôme. [...]
Cela contraste avec la salle plus petite, qui est en réalité un
mausolée intégré à la mosquée. L'intérieur est construit sur une base
carrée d'environ dix mètres, pour une hauteur de vingt. Mais alors que
la plus grande salle témoigne d'une expérience insuffisante pour son
échelle architecturale, la petite incarne ce moment rare qui sépare le pas assez d'expérience du trop d'expérience,
ce moment où les éléments de construction ont été débarassés de toute
masse inutile, mais résistent encore aux séductions d'une grâce
superflue [...] Là se trouve
la perfection de l'architecture, à laquelle on n'atteint pas par la
forme des éléments -simple affaire de convention-, mais par la noblesse
de l'équilibre et des proportions. Et l'intérieur de ce petit
édifice approche de la perfection à un point que je n'aurais jamais cru
possible hors de l'Europe classique."
Robert Byron, Route d'Oxiane
|

sous le dôme Sud
|

sous le dôme Nord
|
|
|
|
|
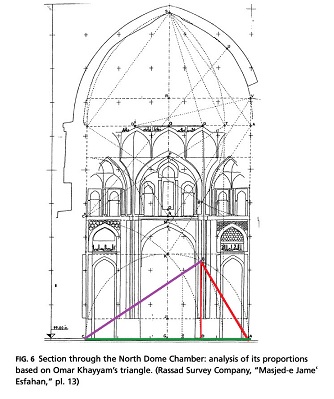
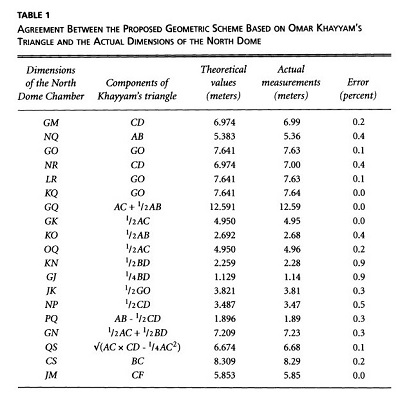
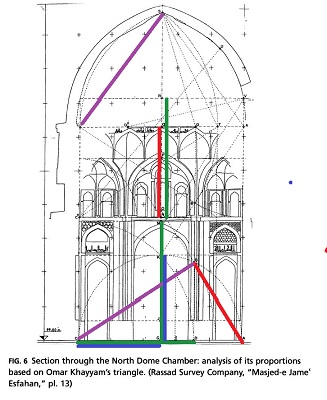
Que nous dit Alpay Ṏzdural des belles proportions du dôme Nord? Dans son article A Mathematical Sonata for Architecture: Omar Khayyam and the Friday Mosque of Isfahan (1998)
il propose d'installer un triangle de Khayyam au pied de la
salle, et rapporte toutes les mesures importantes de cette vue en
élévation aux côtés du triangle (nous avons adjoint à sa figure
quelques égalités avec un "code-couleur": deux segments de même
longueur ont même couleur). Le résultat est assez convaincant, car la
précision est vraiment très bonne!
|
|
|

|
triangle de Khayyam superposé au dôme Nord
|
tableau de Mesures (A. Örduzal)
|
quelques égalités dutableau précédent illustrées
|
photo correspondante (le Mathouriste)
|

|
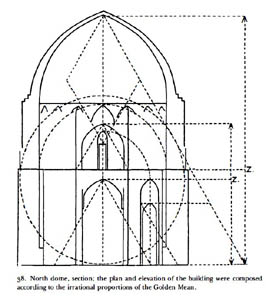
Dans le livre, sans commentaire:
figure empruntée à Eric Schroeder,
qui a noté les éléments en rapport avec Φ
d'un z... qui veut dire Zeising!
|
Mais... si cette
interpétation est la plus récente, ce n'est pas
la seule. Dans le livre qu'il consacre à cette mosquée, Oleg Grabar,
archéologue et historien de l'art américain, reprend une figure de
l'anglais Schroeder, qui voit dans la perfection de cette salle... la
marque du nombre d'or! Qui croire? L'un, l'autre... ou aucun des deux?
A priori, le Mathouriste répondrait:
aucun des deux! Avec une bonne raison: le nombre d'or a engendré une
pléthore de délires, à la suite d'un certain Adolf Zeising et du prince
Matila Ghyka, très justement décrits par Marguerite Neveux dans Le Nombre d'Or, Radiographie d'un Mythe, (petit par
la taille, mais grand par sa qualité et son sérieux). Ils ont couverts
le Parthénon, puis d'autres monuments, de triangles et de cercles
jusqu'à voir apparaître, INÉVITABLEMENT, cette proportion, du coup réputée divine.
Car il y a une bonne et simple raison mathématique à cela: ayant choisi un nombre irrationnel quelconque ζ (aussi bien le nombre d'or Φ que
la racine de l'équation du troisième degré qui détemine le triangle de
Khayyam), les combinaisons à coefficients entiers relatifs
a + b ζ
permettent de s'approcher aussi près qu'on voudra de n'importe quel
nombre réel donné. Autrement dit, à force d'ajouter, soustraire et
multiplier, on finira toujours par trouver le nombre d'or ou le triangle de Khayyam) absolument n'importe où.
|
Néanmoins, si cela disqualifie rapidement la figure de Schroeder, celle d'Ṏzdural
mérite qu'on s'y arrête. Il a certes tracé beaucoup de lignes, mais
seulement parce qu'il étudie beaucoup de longueurs entre points de la
figure: pour chacune, la comparaison aux côtés du triangle de Khayyam
est fort smple, donc il n'y a pas eu de "bricolage calculatoire
forcené" pour y parvenir. Deuxième raison, l'avis d'un expert:
intéressé, mais sceptique et prudent, le Mathouriste avait profité, lors d'un congrès à Bruxelles,
d'une rencontre avec Reza Sarhangi pour lui demander son avis. Ce
mathématicien américain (d'origine iranienne), fondateur des
conférences Bridges vouées,
comme le mom le suggère, à établir des ponts entre arts et
mathématiques, validait sans réserve cet article, dont une variante a
paru dans la revue Nexus.
Sur l'édification de la mosquée, aucun témoignage d'historien XIème siècle
ne cite nommément Khayyam, tout en évoquant comme naturel, de façon
générale, le soutien des mathématiques à l'architecture. Mais qui,
sinon son auteur, pouvait appliquer à ce plan un manuscrit non encore
publié? Si son triangle régit l'harmonie du dôme nord, Khayyam est,
sinon l'architecte, du moins son éminence grise. La probabilité de sa
contribution reste donc très forte.
"On raconte qu'un vizir, étonné d'entendre Omar exiger une somme de cinq mille dinars d'or, lui aurait lancé:
- Sais-tu que je ne suis pas payé autant moi-même?
- C'est bien normal, rétorqua Khayyam.
- Et pourquoi donc?
- Parce que des savants comme moi, il n'y en a qu'une poignée par
siècle. Alors que des vizirs comme toi, on pourrait en nommer cinq
cents chaque année. "
Amin Maalouf, Samarcande
|
Tiens, tiens... cela ne nous rappelle-t-il pas quelque chose?
« Prince, ce que vous êtes, vous l’êtes par le hasard de la naissance. Ce que je suis, je le suis par moi.
Des princes, il y en a eu et il y en aura encore des milliers. Il n’y a qu’un Beethoven. »
— Beethoven à Lichnowsky, octobre 1806.
|
Téhéran
Vénéré par une large part d'une population qui voue un culte à ses
poètes et les tient pour une part essentielle du patrimoine national,
Khayyam ne pouvait qu'être statufié dans la capitale. Rendons
nous donc dans le parc
Laleh, où nous avons déjà croisé Al-Biruni. Sérieux, notre ami Omar, presque trop: on dirait qu'il fait la tête! Mais tournons lentement autour...
... et l'on découvrira peu à peu sa cruche de vin, largement
camouflée par son manteau, mais avec une maladresse calculée: le but
est bien que le spectateur la découvre! Le volumineux ouvrage qu'il
tient est sans doute le recueil des quatrains, mais sous la
cruche, un autre livre... le traité d'algèbre?
Bois du vin. C'est lui la vie éternelle.
C'est le trésor resté des jours de ta jeunesse
La saison des roses et du vin, et des compagnons ivres!
Sois heureux un instant, cet instant, c'est ta vie.
O. K.
|

|
| Days of Wine and Roses... ici avec le vin de Desargues!
à déguster musicalement: la B.O. du film; mais surtout l'immortelle version du trio de Bill Evans |
En dépit de l'aspect quelque peu sulfureux du personnage quant à
l'alcool rigoureusement interdit dans la République Islamique, jamais
il n'a été question d'enlever ou de détruire ce monument.
Hommages ... ou récupérations mercantiles?

|

|

|

|
en Iran
|
quelques exemples de vins... deux égyptiens et un Bordeaux
|
Il n'est pas rare de voir, en Iran, un restaurant baptisé de son nom. Ailleurs, tout particulièrement en Égypte, des
vins essaient d'attirer le chaland avec ce nom magique sur l'étiquette.
En Égypte encore, un luxueux bateau porte son nom en symbole de plaisir et de
volupté: il faut dire qu'il permet de découvrir tous les monuments
nubiens sauvés lors de la mise en eau du grand barrage sur le Nil, en
effectuant des croisières sur le lac Nasser, entre Assouan et
Abou-Simbel, C'est ainsi que le Mathouriste l 'a croisé... alors qu'il effectuait ce (superbe) parcours à bord d'une Dahabieh
traditionnelle, qui joint au cachet d'authenticité l'exceptionnel
avantage de n'embarquer qu'un très petit nombre de passagers.
|

|

|
Grâce à la traduction de FitzGerald,
Khayyam est rapidement devenu célèbre en Occident, voire
starifié... car oui, même Hollywood s'est emparé de sa vie pour en
faire un film! (Authenticité historique non garantie...)
|
|
Apothéose céleste, un satellite, mis en orbite le
9/08/2022 par une fusée russe Soyouz (on imagine mal qu'il eût pu
s'agir d'une fusée américaine...), porte son nom. Ultime
preuve du consensus autour de son nom: en le baptisant ainsi, les
autorités du pays ont voulu mettre sur le même plan deux fiertés
légitimes: celle de l'avancée technologique et celle de l'héritage
historique et culturel, dans toute sa diversité depuis la Perse antique
(La tentation d'effacer le passé pré-islamique, qui a existé lors de la
révolution, n'a été que très éphémère). En détournant le regard des
pratiques peu orthodoxes -au regard de la morale islamique- du héros:
pour cimenter l'union nationale, "Paris vaut bien une messe" chez nous, et Khayyam... une cruche de vin!

|

|
source des images: Roscosmos (agence spatiale russe), trouvées dans cet article.
|
Pour conclure cet épisode...
( Mais ne manquez surtout pas les suivants! Sinon, vous n'atteindrez jamais le Troisième Degré !!! Liens en bas de page )
|
... revenons à Téhéran, au parc Laleh, dans la douceur de la nuit... n'est-ce pas encore plus beau, en se récitant un quatrain choisi?

|
La nuit a dans sa robe un trou de clair de lune.
Bois du vin. On n'a pas toujours cette fortune.
Sois heureux et jouis: après nous, bien des fois,
La lune éclairera nos tombes une à une.
O. K.
|

|
Références de l'épisode
Œuvres de Khayyam
- O. KHAYYAM, Les Rubáiyáts (Behzad)
- O. KHAYYAM, Quatrains (Mille et Une Nuits)
- R. RASHED, B. VAHABZADEH, Al-Khayyam Mathématicien (Blanchard) [ texte original avec trad. française et commentaires]
- F. WOEPKE, L'Algèbre d'Omar Alkayyani (Duprat) [ traduction française, 1851, en ligne sur Gallica-BnF]
Livres
- R. BYRON, Route d'Oxiane (Petite Bibliothèque Payot)
- A. DJEBBAR,
Une Histoire
de la Science Arabe (Points-Sciences)
- A. DJEBBAR, L'Algèbre Arabe : Genèse d'un Art (Vuibert)
- A. MAALOUF, Samarcande (Le Livre de Poche)
- M. NEVEUX, Le Nombre d'Or, Radiographie d'un Mythe (Points Sciences)
- R. RASHED,
Histoire des
Sciences Arabes,t1: Astronomie, t2: Mathématiques
et Physique (Seuil)
Articles




















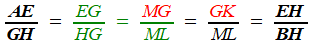
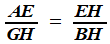 ;
; 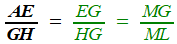 d'une part, et
d'une part, et 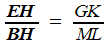
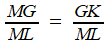 , d'où
, d'où 


















