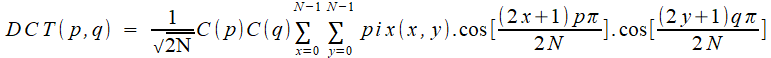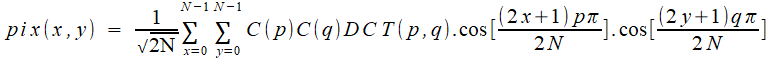Signaux: soudain, votre silhouette est transformée...
... Une Promenade Fouriériste! (Partie 4.2)
Résumé des épisodes précédents: la transformée de Fourier (qu'on peut considérer comme le jeu de coefficients de la série, dans le cas d'une fonction périodique), peut se calculer rapidement, dans sa variante discrétisée FFT, ce qui est bien utile, avons nous dit... mais il serait temps de savoir à quoi!
| cas d'une fonction périodique (série) | cas d'une image | cas d'une erreur... |
 |
 |
 |
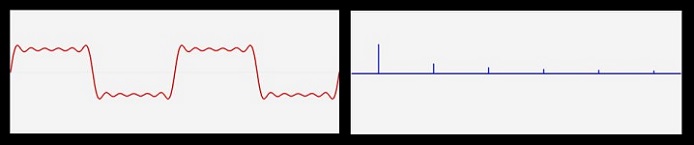
| Dans tous les cas, l'original est à gauche, sa FFT à droite; sauf dans le dernier, où l'original semble perdu... | ||
Les exposés (plus ou moins) techniques pouvant être trouvés en abondance sur la toile, nous nous limitons ici à des principes généraux et des présentations schématiques: le but est d'embrasser d'un coup d'œil ce que Stéphane Mallat appelle respectueusement le Royaume de Fourier.
Parole, parole et... en avant la Zizique!
Nettoyer les Vieux Enregistrements Analogiques
Les amateurs de jazz ont longtemps attendu une restituion améliorée des
enregistrements mythiques qui ont fait l'histoire, tels le West End Blues de Louis Armstrong
ou le Creole Love Call de
Duke Ellington: en dépit d'efforts lors du transfert sur LP 33 tours
des faces gravées sur 78 tours, le gain resté limité -essentiellement,
à une usure moins rapide du nouveau support. Il a fallu attendre
l'avènement du CD, et donc la transcription numérique des
enregistements analogiques,
pour bénéficier de restaurations spectaculaires. Les fans de classique
ont fini par suivre et retrouver le goût du vrai après une période
"d'égarement" dans la quête technique de la pureté sonore, puisqu'on
pouvait ne plus avoir choisir entre l'authentcité crachotante d'un
ancien légendaire et la vacuité ébouissante d'un pyrotechnicien made in China...Cette possibilité d'un bon compromis doit tout au traitement nummérique du signal, qui autorise tous les allers et retours entre le signal temporel et son déploiement en fréquences par transformation de Fourier, est maintenant à la portée de tout un chacun avec le logiciel gratuit Audacity (apparu en 2000; site officiel). Une fois chargé un fichier sonore, on y voit , à l'écoute, défiler le signal en fonction du temps, et l'on peut demander le spectre d'une portion de ce signal qui apparait dans une autre fenêtre... très rapidement! "Monsieur Jourdain 2.0" vient d'effectuer, d'un seul clic, une transformée de Fourier rapide.
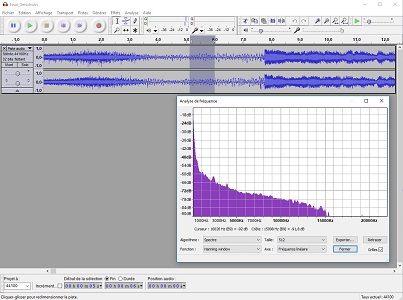
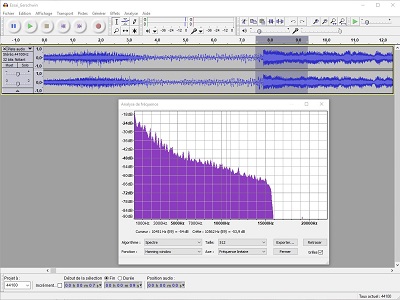
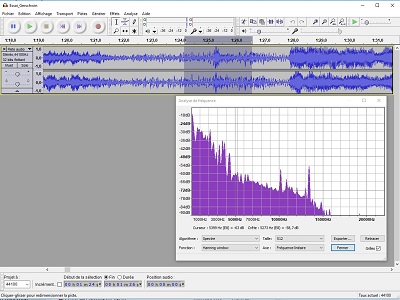
Petite parenthèse de fonctionnement: voici par exemple trois moments de l'ouverture de Candide, de Leonard Bernstein. On choisit une petite portion (bande gris sombre), et l'onglet "Analyse" offre l'option "Tracer le spectre" qui s'affiche dans une autre fenêtre. On peut déjà observer les différences entre un quasi bruit blanc avant le départ (fond de conversationb dans la salle), le départ de l'orchestre, un solo de flûte...
Revenons à la remastérisation. Pour enlever le bruit de fond d'un 78 tours, il "suffira" d'analyser un tout petit extrait entre deux plages, qui mettra enévidence les fréquences de ce bruit, de la même façon que ci-dessus- c'est à dire, par FFT. On peut ensuite demander au logiciel d'enlever cette "signature" de tout l'enregistrement, ce qui doit lui procurer une amélioration notable... Bien sûr, pas de miracle: on enlèvera aussi la composante correspondante des instruments, des voix... mais ce sera sans doute y enlever un petit coefficient, et a toutes chances d'être inaperçu.
Enlever une fréquence donnée est encore plus immédiat, ce qui gommera définitivement un ronflement de secteur (par défintion, à fréquence constante, 50Hz en Europe, 60Hz aux États Unis), ou atténuera un sifflement, souvent très concentré autout d'une seule fréquence. Un craquement repéré à sa position temporelle livrera sa "signature fréquentielle" en isolant une petite portion autour de lui, dans laquelle on essaiera de gommer les plus fortes de ses fréquences. On trouvera même, pour se préparer au karaoké... de quoi enlever une voix, exercice de filtrage un peu plus délicat pour les concepteurs de tous ces petits boutons magiques.
Audacity a des grands frères plus performants (mais cela a un prix!), ou carrément professionnels lorsqu'il s'agit de remastériser les enregistrements historiques. Cela nécessite aussi, aux commandes, des ingénieurs du son experts; et l'expertise ne s'apprend pas en une semaine!
Pour finir sur un exemple
sonore, voici une démonstration d'avant/après sur un enregistrement de
très mauvaise qualité technique, mais de qualité artistique
superlative: Thelonious Monk himself,
en club, jouant les premières notes de Misterioso, thème sorti sur un
album célébrissime par sa pochette, qui empruntait Le Voyant (1915) à Giorgio de
Chirico. Où l'on comprendra que le nettoyage (par le logiciel iZotope RX 2 Advanced, source: ce blog), peut faire beaucoup... mais pas tout.
Mais tout de même: Monk, Chirico, Fourier... what else? |
 |
 original à gauche, remastérisé à droite. Cliquez dessus pour une version audible. |
Compresser les fichiers sons: Requiem pour MP3
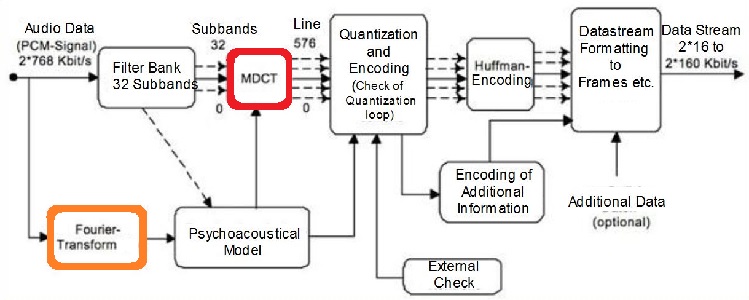
Qu'il s'agisse de disposer d'assez de place pour stocker, ou de parvenir à diffuser un streaming audio en temps réel dans un baladeur, mieux vaut qu'u fichier musical soit le moins gros possible... d'où l'idée de le compresser, le transmettre, et le décompresser à l'arrivée. De sa naissance (1993) à l'annonce de sa mort (2017), MP3 a assuré cette fonction, avec une efficacité redoutable, qui a conduit à faire chuter les ventes de CD au profit de la musique en ligne: certes, quand le consommateur achète un produit que lui-même considère comme "jetable" (imagine-t-on l'incunable ci-dessus dans cette catégorie?) et pour lequel une piètre qualité sonore suffit (imagine-t-on amputer des fréquences au violon d''Arabella Steinbacher ou au sax alto de Johnny Hodges?), la qualité passe au second, voire au troisième plan...Quoi qu'il en soit, la FFT est encore présente à deux endroits du processus d'encodage, assez complexe dans son ensemble: nous ne nous attarderons pas sur l'ensemble, pour ne mettre l'accent que sur les points stratégiques où la transformation de Fourier met son grain de sel. Les voici, encadrés en couleur dans toute la chaîne.
Le signal temporel (un morceau de musique) est d'abord découpé en petits morceaux (quelques secondes), dont on retient 1152=2x576 échantillons. Cest à chacun de ces blocs que va s'appliquer l'algorithme de compression; puis on les mettra bout à bout. À à l'arrivée, découpage et processus inverse.
Le cœur du processus est un passage par un banc de filtres qui "tamise" le signal selon 32 bandes de fréquences; à chacun de ces "sous-signaux" est appliqué la MDCT, ce qui signifie Modified Discrete Cosine Transform: son nom l'indique presque, c'est une transformée de Fourier cosinus (CT), discrétidée (D). DCT est le nom bien usuel de la transformée cosinus discrète, ou approximation de l'intégrale en cosinus de Fourier par une somme finie (avant qu'elle ne devienne Fast par application de la méthode de calcul de Cooley et Tuckey). Le M de Modified fait référence à un léger déplacement des points d'échantillonnage; la MDCT délivre en sortie deux fois moins de valeurs qu'en entrée.
Parallèlement, le signal d'entrée se voit appliquer une transformation de Fourier "classique" -i;e; non modifiée, en version rapide évidemment. On la soumet au "modèle psycho-acoustique" qui la débarasse de fréquences élevées auxquelles l'oreille "moyenne" d'un individu est réputée peu sensible: c'est un premier processus qui va engendrer une compression avec perte. Ses résultats vont permettre de "nettoyer" les résultats de la MDCT, la quantification enlevant les composantes faiblement représentées (en dessous d'un certain seuil; on détaillera plus bas l'exemple assez analogue de JPEG pour les images). Suit un codage de Huffman (plus de détails en anglais!), procédé classique de compression, mais conservative pour ce qui le concerne.
Qui n'a jamais fait une photo au format JPEG?
Pas grand monde, à l'évidence, depuis que la photo s'est faite numérique. Et encore moins depuis que l'appareil photo a eu l'idée de se déguiser en téléphone... Les images stockées ont des noms du type IMG001.jpg, et cette extension ".jpg" désigne le format de fichier le plus courant. Il y en a certes d'autres, à commencer par le format brut, dans lequel une image en noir et blanc (pour simplifier) est un tableau de valeurs de gris, codées entre 0 et 255, une par pixel de l'image. JPEG permet de compresser spectaculairement ce volume de donnés., grâce à la tranformation de Fourier et au prix d'une légère dégradation, qu'on peut rendre imperceptible,| 1. Avant
de
transformer l''image, on la découpe en blocs de 8x8
pixels, démarche comparable (mais en 2 doimensions) à celle appliquée
par MP3 pour comprimer le son. Une image 512x512 (c'était beaucoup, au
temps des
débuts héroïques...) sera donc
partitionnée
en 64x64 = 4096 petits carrés de cette taille, chacun
à
64 pixels. Vérifiez, le compte y est: 512x512 = 4096x64 ! 2. C'est à chacun de ces petits carrés qu'on va appliquer une variante de la transformée de Fourier. Bidimensionnelle d'abord (Fourier avait lui même généralisé à 2 ou 3 dimensions), discrète toujours (évidemment), et limitée à l'emploi des cosinus, d'où son nom de Discrete Cosine Transform (DCT). |
|||
Les
formules peuvent paraître un peu rugueuses; n'en retenons que
l'essentiel (au pire, sautons les...):
Après cet effeuillage, il ne reste qu'une somme (double, pour aller dans les deux sens dimmensionnels) des produits de la fonction pix (qui donne le niveau de gris), et de cos [...] qui prennent la place des exp[i...]. Une transformée de Fourier, quoi! Et la
merveilleuse propriété reste: la
formule inverse est
la même, à quelques broutilles près!
|
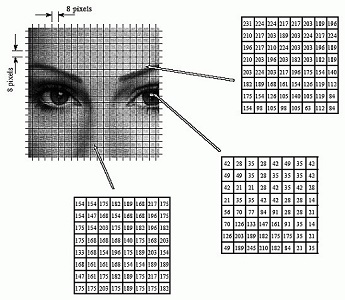 source de l'image |
||
3. À ce stade, on peut légitimement penser qu'on n'a fait que compliquer...
D'autant que la notion de fréquence est bien plus abstraite dans le cas des images que dans le cas du son. Il se passe toutefois quelque chose d'analogue; commençons par un exemple (emprunté au livre de Mark Nelson, La Compression des Données, Dunod); les valeurs sont bien sûr arrondies aux entiers:
La majorité des coefficients à valeur élevée se situent vers le haut et la gauche. Pourquoi? parce que les basses fréquences de l'image encodent l'essentiel des contours, les fréquences plus hautes ajoutant de la précision. Un peu comme pour une voix: les fréquences les plus basses suffisent à la comprendre, et c'était exploité par le téléphone avant l'ère numérique: en coupant les fréquences au delà de 2000Hz, le discours était net, mais si l'on faisait écouter de la musique à son interlocuteur, elle souffrait beaucoup -tout en laissant le morceau reconnaissable. Cela se reproduit avec l'image; la première somme calculée est, à un coefficient près, la moyenne des valeurs du tableau; les autres coefficients encodent des variations plus fines de l'image. De plus en plus fines en s'éloignant vers le sommet opposé du carré.
À ce niveau, la DCT Inverse restituerait exactement la portion d'image; et on na clairement rien gagné en espace, puisqu'on remplace par un tableau de la même taille.
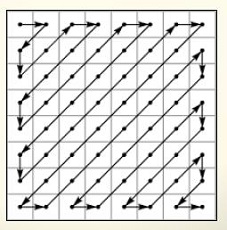
4. Une fois constaté le phénomène, on l'accentue en divisant par un facteur de quantification, qui traduit cet éloignement: en général: comme p et q croissent à partir du coin en haut et à gauche, p+q est constant sur une diagonale montant de gauche à droite, et cellte valeur est d'autant plus élevée que l'on va vers le coin en bas , à droite. On prend en général, 1+a*(p+q+1); a est réglable, par ex a=2, etn arrondit à l'entier le plus proche.
|
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| après DCT et quantification | parcours zig-zag | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Le procédé est clairement irréversible; il y aura donc perte (modérée avec un a bien réglé, mais la compression consistera à éviter de répéter tous ces zéros: un procédé classique, le Run Length Encoding, qu'on ne détaillera pas ici mais facile à imaginer, ne retient de ce tableau que les coefficientts non nuls et la longueur des chaînes de 0 intermédiaires, grâce à un parcours en zig-zag particulièrement bien adapté à l'effet de la quantification!
5. On accède de nouveau à l'image par "déquantification" (produit par l'inverse) et DCT inverse.
En résumé, la transformation de Fourier est intervenue:
- sous forme discrète, mais non "rapide" (pas de FFT);
- pour mettre les tableaux de valeurs de gris sous une forme qui permet la compression.
Qu'est ce qui rend un scanner médical performant?
Introduction égyptienneLes stars aussi passent au scanner! Les nouvelles techniques d'imagerie médicale, après avoir fourni une aide au diagnostic sans précédent, et ainsi contribué à sauver des milliers de vies, ont naturellement étendu leur champ de compétence... à l'archéologie. L'avantage est évident: ce sont des techniques non invasives, qui permettent de voir à l'intérieur d'un objet, d'une sculpture, sans y toucher!
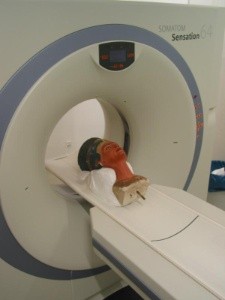
En l'honneur de "Fourier l'Égyptien", commençons avec un des bustes les plus célèbres de l'Histoire de l'Art... et comme vous l'avez vu et revu, le Mathouriste, qui n'aime rien tant qu'un regard décalé, vous le fait voir de façon un peu moins attendue... d'abord, avec une toile qu'il aime particulièrement, car elle confronte deux de ses artistes préférés, l'un auteur, l'autre sujet: le peintre Bernard Rancillac, figure de proue de la Figuration Narrative, et, vous l'aurez reconnu, Alberto Giacometti dans son atelier. Rancillac conçoit ses toiles à partir de photos, découpées, réassemblées, projetées à l'épiscope sur la toile qu'il colore à son gré... et voilà comment une charmante curieuse s'invite chez Alberto! Á droite, cette beauté va faire savoir ce qu'elle a dans la tête, grâce à un passage au scanner (2006, mais une première séance s'était déroulée en 1992, 20 ans après l'invention du scanner médical). Les experts ont notamment pu découvrir le modèle brut en pierre, savoir comment il avait été "stuqué" avant d'être peint (voir cet article), et accessoirement de désamorcer une argumentation fantaisiste prétendant que la statue n'était qu'un faux, âgé d'une centaine d'années seulement.
 |
 |
|
| Bernard Rancillac, "chez
Alberto" (1966) vu à la rétrospective 2017, Espace Niemeyer (Paris) |
photographie originale l'ayant
inspirée: par Sabine Weiss (1954) voir ce site (Musée de la Photographie) |
Néfertiti passe son
examen (voir ici l'article) |
|
"Jusqu'à
cet examen,
nous ne connaissions pas l'épaisseur du stuc, ni ne savions
s'il y avait un deuxième visage sculpté dans la
pierre. L'hypothèse courante était que
celle-ci ne constituait qu'une simple armature."
A. HUPPERT,
directeur del'Institut d'Imageire Scientifique
Hôpital de la Charité, Berlin |
||
Prenez le temps, avant de plonger vos yeux dans le cambouis mathématique, de contempler la reine en écoutant le mythique Nefertiti du Miles Davis Quintet (Wayne Shorter, Herbie Hancock, Ron Carter et Tony Williams aux côtés du maître).
Un scanner, comment ça marche? Et que vient faire Fourier?
Un petit coup d'œil au matériel des premiers temps (1972) et... aux images obtenues dit mieux que des mots, le formidable progrès technique qui a accompagné une innovation presque immédiatement récompensée par un prix Nobel de médecine (1979, Allan M. Cormack, Godfrey N. Hounsfield [plus détaillé en Anglais])
 |
 |
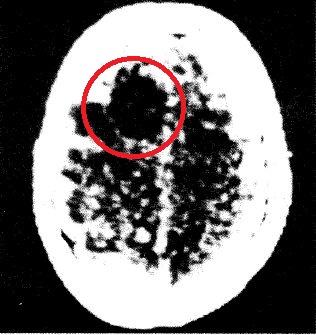 |
| première image d'un cerveau | machine ayant
réalisé l'image de droite. Elle permet seulment le passage d'une tête...aujourd'hui le corps entier! |
première image d'une tumeur cérébrale |
| Source des images: discours
de réception du prix Nobel,
rédigé par Hounsfield. |
||
Au départ, le principe ne diffère pas d'une radiographie ordinaire. Celle-ci permet de bien distinguer un os dans un environnement de muscle et de graisse, parce qu'avec une capacité d'absroption supérieure des rayons X, il apparait comme une tâche plus sombre. On vise bien le même but pour voir une tumeur dans un cerveau atteint, mais les différences de niveau de gris sont moindres.
Mais l'essentiel du problème est ailleurs: une projection d'un objet de l'espace sur un plan perd l'information spatiale en écrabouillant tout! Sur toute sa trajectoire linéaire, un rayon X "somme les atténuations" en chacun des points et délivre un résultat global, sans qu'on puisse revenir en arrière pour séparer les contributions.
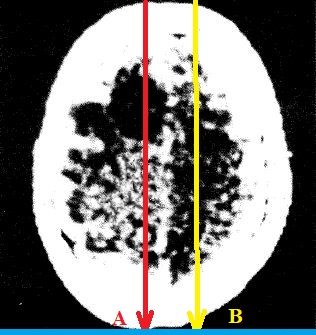 |
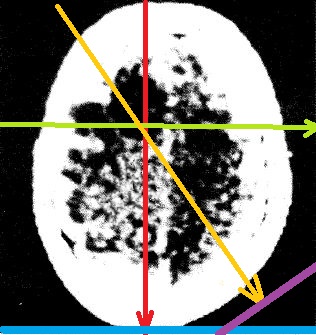
Sur toute sa trajectoire linéaire, un rayon X "somme les atténuations" en chacun des points et délivre un résultat global, sans qu'on puisse revenir en arrière pour séparer les contributions. Sur la figure de gauche (image "historique" modifiée pour les besoins de notre démonstration), les sommes présentées sur la droite bleue, au point A par le rayon rouge, au point B par le rayon jaune, peuvent fort bien être égales, donc n'apporter aucune information au médecin, alors que ces sommes ont été obtenues de façons radicalement différentes: l'une (rayon rouge) par une grosse contribution (70% à 80%) dans la partie sombre suspecte et le complément dans les zones assez claires restantes; l'autre (rayon jaune) de manière plutôt uniforme. Dans ces conditions, comment le médecin pourrait-il savoir que l'un traverse une zone tumorale, l'autre une zone saine? À droite, une analogie numérique: donnons nous 4 nombres: a, b, c,d, dont nous connaissons les sommes par colonne: pouvons nous les déterminer, inversement? Bien sûr que non! a
+ c = b + d = 40
Nous n'avons que
deux équations pour quatre inconnues, il y a des tas de
manières de réaliser cela.
|
|
||||||||||||||||||
 |
À droite, restons-y, une information sur les sommes en ligne élimine une partie de l'indétermination. Par exemple, a = 15, b = 17, c = = 25, d = 23, n'est plus envisageable. Mais le système a
+ c = b + d = 40
en conserve une certaine part, car l'équation a + c + b + d = 80,
qui résulte des sommes de colonnes, détermine c + d = 24
dés qu'on connait a
+ b = 56. Autrement
dit, la dernière équation n'apporte aucune
information
supplémentaire. Le système se
réduit en
fait à 3 équations, par exemple:a + b = 56, c + d = 24 a
+ c = b + d = 40
a + b = 56 Mais avec une somme de ligne et une diagonale, par exemple: a + c = b + d = 40
a + b = 56 a + d = 52 on trouve
facilement tous les éléments du tableau de
manière unique, à savoir
a = 34, b =
22, c = 6 ,
d = 18
|
pas tout à fait assez...
gagné!
|
||||||||||||||||||
Repassons à l'image de gauche: pour avoir quelque espoir de reconstituer les valeurs des niveaux de gris en tout point de cette coupe, il vient l'idée qu'il faut connaître les sommes dans plusieurs directions, beaucoup de directions... en fait tous les angles possibles. Et voilà pourquoi le scanner a une forme d'anneau!
Ce n'est pas gagné pour autant, car les choses sont, bien sûr, plus compliquées. Il faut trouver une fonction inconnue d(x, y) qui représente la densité de gris au point (x, y) de l'image précédente en connaissant les fameuses sommes dans toutes les directions, qui s'écrivent maintenant avec des intégrales

où (X, Y) sont les
coordonnées dans le repère ayant
tourné de l'angle θ, D traduisant d dans ce
système de coordonnées. La chose s'annonce ardue!
Mais ce qui est impossible dans les coordonnées "naturelles" d'espace devient possible dans l'espace des fréquences, c'est à dire après transformation de Fourier!
Un théorème, dit théorème de rétroprojection, vient opportunément relier les deux transformées, celle, unidimensionnelle, de Pθ pour toute les valeurs de θ et celle, bimensionnelle, de d.
Mais ce qui est impossible dans les coordonnées "naturelles" d'espace devient possible dans l'espace des fréquences, c'est à dire après transformation de Fourier!
Un théorème, dit théorème de rétroprojection, vient opportunément relier les deux transformées, celle, unidimensionnelle, de Pθ pour toute les valeurs de θ et celle, bimensionnelle, de d.
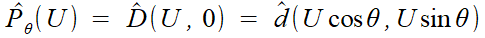
| explication
détaillée <à
venir>
|
On reviendra à d par la formule de réciprocité de la transformée de Fourier bidimensionnelle; c'est à dire
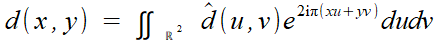
En effectuant des coupes successives, grâce à l'avancée par échelons du "lit" à l'intérieur de l'anneau, on obtient une reconstituion tridimensionnelle, qui peut donner lieu à des images en perspective de l'objet etudié, qu'on peut même animer par rotations successives!
Mais revenons à l'Egyptologie...
Avec deux exemples fameux.où le scanner et sa FFT ont apporté une aide décisive. Et d'abord, la célébrité qu'on ne présente plus, qui fut la première momie radiographiée... puis la première à passer au scanner:
|
"Notre technologie a pour but, avant tout, d'améliorer le suivi médical des patients dans le monde entier. Cependant, nous sommes heureux de contribuer aux efforts de ceux qui cherchent à percer les mystères de l'archéologie. Voilà deux ans que nous avons scanné la momie de Toutankhamon, et maintenant, nous apportons notre aide à l'étude d'un autre trésor de l'ancienne Égypte." B.
MONTAG, président
de Siemens Medical
Solutions
|
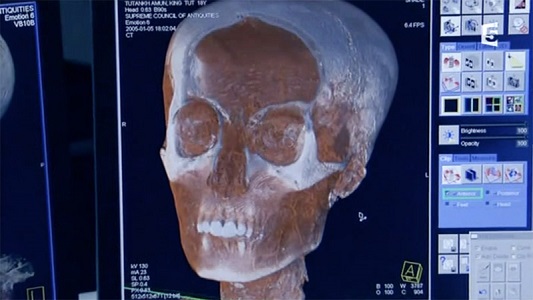 scanner du crâne de
Toutankhamon, reconstruction 3D.
Source de l'image: cet aticle |
Deuxième exemple, choisi parce qu'il est un cas très récent (2012) où cette technique a permis de résoudre une véritable énigme historique: la mort de Ramsès III.
| Intrigués par une épaisseur de tissu tout à fait inusuelle autour du cou de la momie, mais non autorisés à l'enlever -il est interdit de "déshabiller" la momie, les scientifiques qui l'étudient n'ont plus qu'une ressource pour percer le mystère de cette singularité: examiner le pharaon au scanner... | ||
Toutes ces images sont des captures d'écran de ce vidéo-reportage que nous vous invitons à visionner (3') |
||
|
et c'est ainsi qu'ils
découvrent que Ramsès III a eu la gorge tranchée; la blessure, très
profonde, a dû entraîner une mort instantané: un membre de l'équipe
fait voir que la trachée a été sectionnée en dessous du larynx.
L'hypothèse du complot du harem se trouve ainsi validée.: Et le crime apparut au scanner, titra Sciences & Vie à cette occasion.
Voilà donc comment deux siècles après avoir été l'un des fondateurs de l'égyptologie (voir notre page: Fourier l'Egyptien), Fourier est encore à la pointe pour aider les chercheurs du domaine! |
||
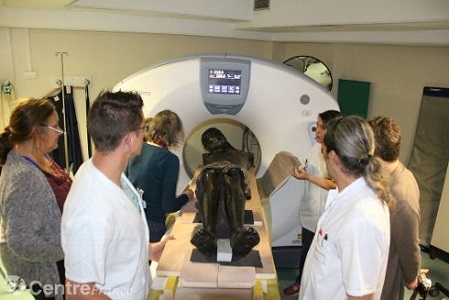
Et puis, ces techniques se démocratisent et se répandent, et c'est tant mieux: de nos jours, sur le territoire français, on n'est jamais très loin d'un scanner, ce qui est crucial pour qu'il n'y ait pas une médecine des riches et une des pauvres, une des villes et une des champs... En voici une preuve archéologique, si l'on ose dire: même au fin fond de l'Auvergne natale du Mathouriste, là où les christs sont noirs... comme les charbonniers du pays, ces bougnats aux curieuses enseignes dans le Paris de jadis: Vins et Charbon, le scanner est aussi devenu un outil d'aide aux historiens de l'Art!
 |
 |
| Images illustrant cet article du quotidien La Montagne (16/06/2016 ) : "Le Christ noir de la cathédrale de Saint-Flour est passé au scanner" | |
Quid de l'IRMN?
Les techniques
d'imageire se sont diversifiées, notamment avec
l'arrivée de l'IRMN. Avec celle-ci, qu'on ne
détaillera pas dans cette page, les détecteurs
reçoivent des signaux, dont il faut
démêler les fréquences...
grâce à la FFT, et c'est une nouvelle fois par
transformée de Fourier inverse que l'on reconstruit l'image
compréhensible par les médecins... et le reste
des humains!
< détails à venir bientôt!>Applications "Optiques" en cristallographie, spectroscopie, astronomie...
sont à retrouver dans la page suivante!Références
- J. COOLEY, The Re-Discovery of the Fast FourierTransform Algorithm (Mikrochimica Acta, 1988)
- J. COOLEY, J.TUKEY , On the Origin and Publication of the FFT Paper (1993)
- J.R. DELLER, Tom, Dick, and Mary Discover the DFT ( IEEE Signal Processing Magazine, Avril 1994)
- M. HEIDEMAN, D. JOHNSON, C. BURRUS, Gauss and the History of the Fast Fourier Transform ( IEEE ASSP Magazine, Avril 1994)
- D. ROCKMORE, The FFT: An Algorithm the Whole Family Can Use (Computing in Science & Engineering, 2000, IEEE)
- J.L. ROCH, La Transformée de Fourier en Algorithmique: Discrète et Efficace (LIG/INRIA Grenoble)
- E. BRIGHAM, The Fast Fourier Transform and its Applications (Prentice Hall)
- H; GOLDSTINE, A History of Numerical Analysis from the 16th through the 19th Century (Spinger)
Poursuivre...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Revenir à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Revenir à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
ller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique
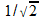 ):
): 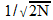 devant
est normalisé
pour que
les deux formules soient le plus similaires possible. Attention, d'un
ouvrage à l'autre, ces normalisations peuvent varier!
devant
est normalisé
pour que
les deux formules soient le plus similaires possible. Attention, d'un
ouvrage à l'autre, ces normalisations peuvent varier!