Kelvin, l'Analyse Harmonique et les Marées

Une Promenade Fouriériste... au Bord de la Mer!

La marée, je l'ai dans le cœur
Qui me remonte comme un signe
...
Une mathématique bleue,
Dans cette mer jamais étale
D'où me remonte peu à peu
Cette mémoire des étoiles

Léo Ferré, La Mémoire et la Mer (1970)

N'hésitez pas à prendre le temps de voir et d'écouter l'auteur, en tête à tête avec son piano; et comme les grandes chansons et les grands interprètes sont faits pour se rencontrer, pourquoi ne pas savourer aussi les versions différentes, forcément, mais avec quel goût, quelle pudeur, quel sens de l'hommage, de Bernard Lavilliers ou Catherine Ribeiro.

Et maintenant, vous devez être plus serein pour aborder le face à face entre marées et Analyse de Fourier, magistralement arbitré par William Thomson, alias Lord Kelvin (1824-1907). Qui a conçu deux appareils, l'un d'analyse du signal -en l'occurence, la hauteur de la marée dans un port donné, l'autre de synthèse -un prédicteur des marées à venir- si efficaces qu'ils ont, un temps au moins, survécu face aux ordinateurs!

Vous pouvez d'ailleurs sauter, en première lecture, les détails techniques pour vous laisser aller à la seule admiration de ces merveilleuses machines...


L'analyseur harmonique des marées conçu par Kelvin. Londres, Sciences Museum	Kelvin. vu par Raoul Dufy: in La Fée Électricité Musée d'Art Moderne, ville de Paris	Son prédicteur de marées. Londres, Sciences Museum

Prédire les horaires des marées: c'est bien le problème pour les marins en général, qui doivent en être informés pour quitter et rallier les ports, et la Grande Bretagne du XIX^ème siècle en particulier, dont la puissance économique -et militaire- est tributaire de connaissances précises sur ce point. On comprend dès lors mieux que la question ait mobilisé un de ses meilleurs physiciens.

Modèle(s) Mathématique(s) des Marées

A priori, parler d'Analyse de Fourier dans ce contexte peut surprendre, car la marée n'est pas un phénomène périodique. Pourtant, elle est la somme d'influences qui, elles, sont périodiques: de la lune et du soleil essentiellement.
Mais voilà: ces diverses périodes ne sont pas commensurables, c'est à dire, n'ont pas un rapport rationnel grâce auquel une période commune, plus longue, pourrait être trouvée. Les deux situations sont illustrées par deux exemples simples ci-dessous.

	équation	périodes des constituants	période
exemple 1	f(t) = 2 sin (t/6) + 3 sin (t/8)	T₁ = 12 π ;.T₂ = 16 π	.T = 48π
exemple 2	f(t) = 2 sin t + 3 sin (t √2)	T₁ = 2 π ; T₂ = √2 π	NON

Le cas des marées s'apparente à notre exemple 2, sauf qu'il y a beaucoup plus de termes, 7 à 10 dans la théorie de Kelvin, une quarantaine, voire une une centaine dans les modèles utilisés aujourd'hui dans les ordinateurs. Chacun correspond à une influence diurne ou semi-diurne (c'est à dire se manifestant deux fois par jour) de la lune ou du soleil: les facteurs prépondérants viennent du mouvement moyen des deux astres (mouvement apparent dans le cas du soleil), mais des corrections concernent chacun d'eux et sont responsables de termes d'importance décroissante, pris en compte ou négligés suivant la précision recherchée.

Voici, à gauche, les dix facteurs d'influence retenus par Kelvin pour construire son prédicteur; à droite, la table numérique des caractéristiques relevées pour un port des U.S.A., Bridgeport (Connecticut); les termes y sont classé par amplitude décroissante. Le terme prépondérant est, sans surprise, celui du à une rotation circulaire de la lune autour de la terre, noté M2; il se lit:

M2 = 3.185 cos (28.984 t - 127.24)

Symbol         speed       amplitude   phase at 
                                      midnight, 9/1/91   

  M2     2T-2s+2h = 28.984    3.185     -127.24
  N2   2T-3s+2h+p = 28.439    0.696      263.60
  S2           2T = 30.000    0.538     -343.66
  K1          T+h = 15.041    0.295      142.02
  L2    2T-s+2h-p = 29.528    0.277       -4.72
  O1       T-2s+h = 13.943    0.212      505.93
  Sa            h = 0.041     0.192      301.50
 \nu2  2T-3s+4h-p = 28.512    0.159       45.70
  K2        2T+2h = 30.082    0.144       -2.55
  Mm          s-p = 0.544     0.108       86.82
  P1          T-h = 14.958    0.102      340.11

T: rotation terrestre (sur son axe)
h: rotation terrestre (autour du soleil)
s: rotation lunaire (autour de la terre)
p: précession du périgée lunaire

Ainsi, Kelvin, et les successeurs qui perfectionnent son modèle (notamment George Darwin qui a fixé en 1883 les notations utilisées) prennent un modèle de la forme

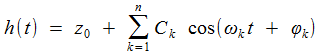
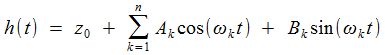
C'est Kelvin lui-même qui emploie le mot harmoniques pour les diverses composantes, quoiqu'elles ne soient plus multiples d'une même fondamentale. Les périodes des constituants, puisqu'elles sont elles-mêmes exprimées à l'aide de périodes astronomiques, sont parfaitement connues. L'enjeu est donc de passer:

de h aux A_k et B_k, c'est la tâche dévolue à l'analyseur;
des A_k et B_k, à de nombreuses valeurs de h(t) c'est celle du prédicteur.

Le travail s'annonce donc similaire à l'analyse harmonique de Fourier, sauf qu'une nouvelle difficulté surgit dans le premier cas: comment calculer les coefficients? Y a-til un substitut pour les formules de Fourier dans ce cas non périodique?
Il peut être instructif de regarder ce qui se passe sur un prototype du genre de l'exemple 2 ci-dessus:

f(t) = A sin t + B sin (t √2)

On peut certes calculer l'intégrale de f(t) sin t , mais... entre quelles bornes? Et plus de relation d'orthogonalité pour annuler celle de sin t . sin (t √2), donc tirer A immédiatement... Cependant, si l'on intègre entre 0 et T, seul le premier terme aura une contribution non bornée (le calcul, facile, repose sur la même linéarisation). D'où une manière de trouver A (et, de façon similaire, B), adaptée, mais sauvegardant l'esprit des formules de Fourier:

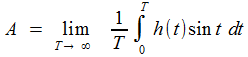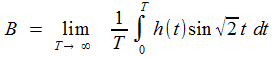On devine alors sans peine l'adaptation au cas général; la démonstration est similaire.

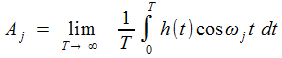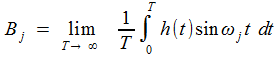et voilà le problème résolu... en théorie seulement!

Remarque: cette théorie a été étendue à des séries, donnant naissance au concept de fonction presque périodique, inventé (1923) et étudié par Harald Bohr (Danois, 1887-1951). Attention, un Bohr peut en cacher un autre: il souffre un peu de l'ombre du prix Nobel (en Physique) de son frère Niels (1922)!

Au sens de Bohr, une fonction presque périodique est une limite uniforme de "polynômes triginométriques" du modèle ci-dessus. On peut les développer en série, conserver les formules de calcul des coefficients ci-dessus; ils prennent alors logiquement le nom de coefficients de Fourier-Bohr. On conserve aussi une formule de Parseval.

Niels et Harald (photo sur le site du Niels Bohr Institute)

L'Analyseur Harmonique de Kelvin


Lord Kelvin, buste par A. McFarlane Shannann (Londres, Sciences Museum)	Prêt à calculer 7 coefficients ( Londres, Sciences Museum)

Voici comment l'auteur présente lui-même sa machine:

Substituer de la matière cuivrée à la matière grise: l'expression est non seulement jolie, elle reflète aussi la technologie de construction des instruments de précision héritée de la tradition horlogère des siècles antérieurs. Clairement, il s'agit de mécaniser ce calcul! Si l'on devine sans peine qu'à la limite, on substiuera un T "assez grand" et que les valeurs de h seront fournies à partir d'enregistrements de la marée (Kelvin décrit, dans son § I, ses propres perfectionnements de la jauge à flotteur, reliée à un style encreur qui trace l'évolution sur un cylindre mû par un mécanisme d'horlogerie) , reste le plat de résistance: le calcul de l'intégrale du produit. Il attribue à son frère James le principe de cette machine:


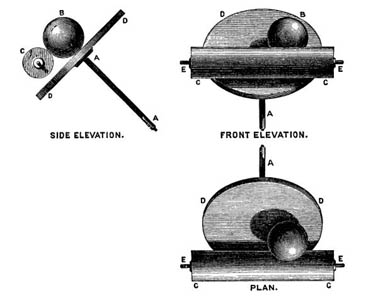
Lord Kelvin, Texte de Présentation de l'Analyseur Harmonique des Marées in Mathematical & Physical Papers, vol. 6 (Cambridge University Press), pp. 272-297	Kelvin, un enregistrement et le dispositif "Disque-Sphère-Cylindre". Londres, Sciences Museum

Le principe de fonctionnement dérive de celui d'un appareil plus simple, le planimètre à cône, dont le but est de calculer la surface délimitée par une courbe parcourue par un style, que voici:


Planimètre à cône (Clair, Paris 1830) Londres, Sciences Museum	Panneau explicatif du fonctionnement. Exposition "Prendre l'Aire", Musée des Arts & Métiers (Paris)

Selon la hauteur sur le cône, qui est proportionnelle à f(x), la roulette tourne plus ou ou moins; très précisément, une "petite" avancée dx le long de la courbe de traduit par une rotation infinitésimale de la roulette (proportionnelle à)

dθ = f(x).dx

La variation totale de l'angle lors du parcours de la courbe somme toutes ces variations; elle est donc proportionnelle à l'intégrale de h.
Ce type d'appareil a par la suite été perfectionné sous divers avatars, décrits en détails dans l'ouvrrage d'Henri de Morin cité en référence, jusqu'au système des frères Thomson, qu'il présente ainsi:

Les Détails Techniques de l'Intégrateur (Calcul Mécanique des Coefficients de Fourier-Bohr)


Détail du dispositif "Disque-Sphère-Cylindre", remarquer la fourche qui pilote la sphère. Londres, Sciences Museum	Gravure représentant l'ensemble in Thomson & Tait, Treatise on Natural Philosophy, vol. 1, part 1	Schéma de principe in H. de Morin, Les Appareils d'Intégration

Le disque tourne à une vitesse x(t) proportionnelle à une primitive de sin ω_jt ou cos ω_jt, le centre de la sphère (guidé par une fourche) étant maintenu à une distance proportionnelle à h(t) de celui du disque. L'inclinaison à 45° de ce dernier, qui saute aux yeux, n'a d'autre utilité que d'optimiser l'appui des surfaces les unes sur les autres, de manière à engendrer un roulement sans glissement. Lequel permet d'écrire l'égalité des vitesses tangentielles sur deux surfaces en contact:

	disque D	sphère B	cylindre C
rayon		R	ρ
vitesse angulaire	x = x(t)	ψ	φ
contact D/B	K h(t) dx = R dψ
contact B/C		R dψ = ρdφ
synthèse	ρdφ = K h(t) x'(t) dt

Sommant ces variations infinitésimales, la variation d'angle totale de est donc bien proportionnelle à l'intégrale de h(t) x'(t) , soit à h(t).cos ω_jt ou h(t).sin ω_jt selon le cas.

Restent encore deux détails techniques à régler. En premier lieu, comment obtenir une vitesse de rotation proportionnelle, non à t ou nt, mais à leur sinus (ou cosinus)? Kelvin emploie pour cela un mécanisme de crémaillère décrit avec plus de détails ci-dessous; pour le résumer, un mouvement de rotation uniforme en t fournit par projection un mouvement harmonique de translation (ie proportionnel à sin t), que la crémaillère sur roue dentée retransforme en rotation à cette vitesse.


Principe général ( x quelconque)	Adaptation à x = sin t (ou cos t)	Adaptation à x = sin nt (ou cos nt)
source : H. de Morin, Les Appareils d'Intégration

En second lieu, il convient de produire, grâce à un mouvement d'horlogerie, des vitesses angulaires aussi proches que possible de celles des astresresponsables; il s'agit donc le les approcher par un rapport rationnel ... seul réalisable avec des dents d'engrenages! Kelvin présente la solution aimablement fournie par M. Roberts, du Bureau des Almanachs Nautiques


Données à approcher	Qualité de l'approximation retenue

Il n'y a plus... qu'à donner le mode d'emploi!

" Pour faire fonctionner la machine, l'opérateur tourne de sa main gauche la roue d'entraînement, et de sa main droite actionne la pointe traçante, qui commande le déplacement longitudinal de la barre portant les fourches des sphères. Sa main gauche tourne toujours dans le même sens, à une vitesse aussi constante que possible de façon à ce que la droite, qui va et vient dans un sens et l'autre, suive exactement avec la pointe d'acier la courbe de marée tracée sur le papier enroulé sur le tambour cylindrique, mu à une vitesse proportionnelle à celle de la main gauche de l'opérateur.
Les onze petits compteurs des cylindres en face des disques doivent être remis à zéro au début de l'opération, et relevés de temps à autre durant l'opération, afin de donner la valeur des onze intégrales pour autant d'instants que l'on souhaitera."

Kelvin conclut en signalant une application déjà réalisée, plus simple puisque dévolue au calcul d'une vraie série de Fourier, destinée à estimer la déviation d'une boussole dans un navire à coque métallique.

analyseur à 5 termes (source inconnue)

Le Prédicteur de Kelvin

Le problème de la synthèse peut, en comparaison, sembler beaucoup plus simple: les coefficients étant connus pour un port (en ayant fait tourner l'analyseur), calculer, mais pour de nombreuses valeurs du temps t,

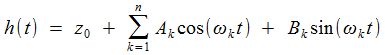
C'est un calcul long: un seul instant t requiert une dizaine de lectures dans une table trigonométrique, autant de produits -peu commodes- et de sommes... Le risque d'erreurs en est d'autant plus élevé.

"Le but est de prédire les marées pour n'importe quel port pour lequel les composants de la marée ont été déterminés par l'analyse harmonique à partir de relevés : non seulement de prévoir les horaires des hautes et basses eaux, mais la profondeur à n'importe quel instant, de manière à pouvoir la représenter par une courbe continue, pour un an, voire un nombre d'années fixé à l'avance."

Lord Kelvin

Il peut donc être utile de le mécaniser! Voici en raccourci l''évolution de l'idée en trois étapes, du tout premier schéma de l'auteur dans sa communication à la Royal Society (1872, mais publié en 1882), à la machine conservée au Musée des Sciences de Londres.


modèle n°1 (approximatif): rotation des centres des poulies supérieures	modèle n°3 (exact): translation (harmonique) des centres des poulies supérieures

Dans la partie du texte ci-contre, Kelvin décrit le principe de sa machine; il raconte aussi comment il a finalisé son idée lors d'une discussion avec un ingénieur, dans un train, en 1872, alors qu'ils se rendaient tous deux à un congrès. Les idées essentielles sont les suivantes (voir le croquis du modèle n°2 ci-dessus): Grâce aux engrenages en partie basse, la rotation de la manivelle engendre des rotations à des vitesses angulaires (et périodes) proportionnelles à celles des divers composants de la marée. Par des cames (on détaillera plus loin ce processus), ce mouvement angulaire ωt est transformé en mouvement harmonique sin ωt de la tige verticale correspondante. Grâce à un réglage initial (valeur du coefficient), la poulie en haut de la k^ième tige monte et descend de la valeur de la k^ième composante de la marée. La sommation est alors réalisée "naturellement" à l'extrémité du câble qui passe successivement dans toutes ces poulies: un style qui lui est fixé, monte et descend proportionnellement à la fonction h(t).

Vues de détail sur le fil "calculant" la somme, son passage sur les poulies... et la manivelle de commande (Londres, Sciences Museum)

Additionner / Soustraire ... avec un fil et des poulies?
Un jeu d'enfant!

Cela peut surprendre au premier abord, mais le comportement additif est très élémentaire, réalisable et utilisable par un enfant à l'école primaire!
Expliquons la chose en deux croquis


situation initiale	mouvement de M₂: h vers le haut	mouvement de S₂: h' vers le bas

Monter la poulie M₂ d'une hauteur h raccourcit de deux longueurs h, chacune de part et d'autre de la poulie, le fil au niveau de cette poulie. Sa longueur totale étant fixe, la pointe traçante descend de 2h sur le cylindre enregistreur. (figure centrale)
Le même travail autout de S₂, avec une hauteur h', ferait, s'il était seul, descendre le style de 2h'. Conjugué avec le premier mouvement, il ferait descendre la pointe de 2h+2h': ainsi, on additionne les effets des deux poulies. Mais si S₂, au lieu de monter, descend de h', alors la variation totale de la pointe traçante est 2h-2h'. (figure de droite)
Avec 10 poulies, on obtient clairement l'addition (ou soustraction) de 10 termes.

Il ne reste plus qu'à expliquer (ci-dessous) comment rélaliser des variations de hauteur qui, au lieu d'être constantes comme dans cet exemple, sont du type h = A sin ωt

Kelvin n'hésite pas à expliquer préalablement que la motivation première, pour ce modèle plus élaboré, réside dans la complexité des marées dans les ports lointains de sa Gracieuse Majesté, Impératrice des Indes


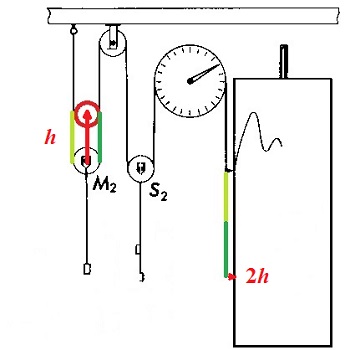
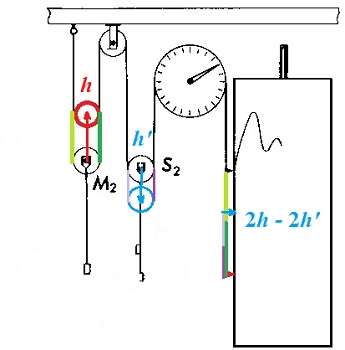
Le nom du fabricant, mentionné à plusieurs reprises, apparait aussi sur le cadran-calendrier.

Le cas, par sa difficulté, exige que soit réalisé exactement, pour chaque centre de poulie un mouvement vertical harmonique, c'est à dite en Asin ωt .
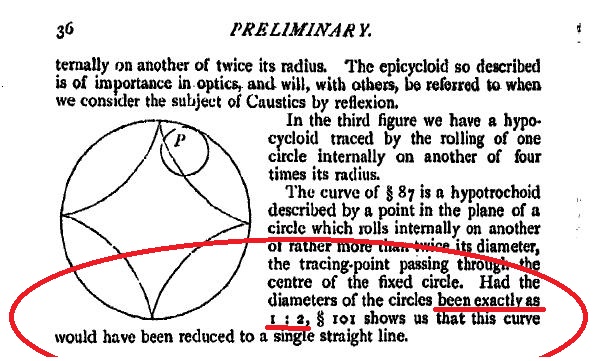
C'est pourquoi il aborde ce point au tout débur de la partie III, consacrée à l'appareil prédicteur... pour dire que c'est un problème fort classique, pour lequel il renvoie au célèbre traité dont il est cosignataire:
W. THOMSON, P. TAIT, Treatise on Natural Philosophy, vol. 1, part 1
Dans cette référence, le mouvement rectiligne harmonique est engendré comme cas particulier d'une hypocycloïde (voir ci-dessous).
Son article sur la machine prédictive signale, sans le moindre schéma, un système de came dont la rainure réalise la projection orthogonale H d'un boulon B, fixé sur un disque tournant uniformément à la vitesse ωt, sur l'axe qui porte le mouvement vertical.
H a donc pour coordonnée sur cet axe Asin ωt (ou Acos ωt ): c'est la simple traduction mécanique de la définition du sinus (ou du cosinus)!

	sinus mécanique... d'après une image de Wikipedia, article: Tide Predicting Machine

Dans le Treatise on Natural Philosophy, une hypocycloïde un peu particulière!

Mais... quelle est cette solution? N'a-t-elle pas un air de déjà vu?
SI, bien sûr! C'est le célèbre couple d'Al-Tusi! Après avoir été outil théorique dans le De Revolutionibus de Copernic, le voici célébré d'un point de vue mécanique concret.

Les détails mécaniques de la conception sont mieux en évidence sur cette machine américaine de William Ferrel:


came commandant le mouvement harmonique vertical de la poulie	chaîne "totalisatrice"	Réglage, par l'opérateur, d'amplitude et de phase d'une composante

Ultime trésor mathématique de la machine, Kelvin revient sur l'approximation rationnelle des rapports de vitesses angulaires. Mais non seulement la liste est ici plus longue que dans la section relative à l'Analyseur, mais l'auteur se fait plus précis sur la méthode employée pour déterminer ces valeurs: il affirme avoir utilisé les convergents ( "converging fractions") des développements en fractions continues.

Certes, la technique n'est pas nouvelle, puisqu'elle est attestée depuis la Grèce antique (Mécanisme d'Anticythère). Mais il est toujours sympathique de voir une nouvelle application horlogère d'un principe simple et performant, où les mathématiques démontrent leur efficacité en évitant de longs tâtonnements.

Page recomposée à partir de W. THOMSON (Lord KELVIN), Mathematical & Physical Papers, vol. 6
pp 294-295

"La machine peut sans difficulté être actionnée à une vitesse suffisante pour assurer en quatre heures le tracé de la prévision des marées pour un an, et ce pour n'importe quel port."

Lord Kelvin

Une démonstration sous forme d'Applet Java est disponible ici; elle est l'œuvre de Bill Casselman pour l'AMS (American Mathematical Society ), et accompagnée d'explications de fonctionnement.
Vous pouvez aussi regarder ces deux vidéos d'un prédicteur en action: partie I, partie II.


Quelques captures d'écran: où l'on voit les poulies monter et descendre!

Des variantes, essentiellement dans le nombre de termes pris en compte, ont été construites aux U.S.A., en Allemagne, en Angleterre même par Roberts et Légé, les assistants que mentionne Kelvin dans son article.

la machine n°2, USA 1912

Elles n'ont été réformées qu'entre 1965 et 1970 lors de la montée en puissance des ordinateurs (mémoire ET calcul); auparavant, la "deuxième machine" des USA, mise en service en 1912, tenait, avec ses 37 constituants et sa double rangée de poulies calculant simultanément les marées haute et basse, la dragée haute aux futurs géants du calcul électronique:

"Pendant la décennie 1950-1960, les programmes de prédiction des marées qui tournaient sur l'IBM 350 ou l'IBM 1620 mettaient plus de temps à fournir leurs résultats que la machine mécanique dont on tournait la manivelle à la main, et c'était profondément déprimant pour les gens d'IBM qui y travaillaient . "

P. ZETLER, The Evolution of Modern Tide Analysis and Prediction- Some Personal Memories (1987)

Fort heureusement un bon nombre de modèles a pu être sauvegardé dans des musées (exemple à Liverpool, Mûnich, U.S.A.). Ce diaporama d'une conférence de P. WOODWORTH (National Oceanography Centre, Liverpool) en présente un grand nombre d'exemples, avec leur dates de fabrication.

La Machine de Kelvin et le D-Day (6 Juin 1944)

Un très intéressant article de Bruce Parker (sur le site Physics Today) dévoile à tout lecteur capable de lire un article généraliste en Anglais le rôle important joué, pour optimiser le choix de la date du Débarquement, par la machine de Kelvin (et l'originale de 1872, sil vous plaît! - Il est vraie "doppée" en 1942 pour traiter 26 composantes pluôt que 10) et une machine conçue par Roberts en 1906. Les deux machines avaient été le plus possible éloignées l'une de l'autre dans le bâtiment de l'Amirauté afin de limiter les risques en cas de bombardement, et, concernant les ports anglais, l'Amirauté disposait de deux ans de résultats d'avance.

Une note de 1943 demanda le calcul urgent de prévisions d'Avril 1944 à Juillet 1944... pour un point désigné par le nom de code: Position Z. N'étaient fournies que les pulsations d'origine astronomique ω_jrelatives au lieu... certainement le meilleur moyen de le tenir secret! Ces constantes sont désignées par leur nom habituel, on le voit ci-contre.
Mais... comment celles-ci avaient-elles été obtenues? L'Amirauté Britannique en disposait pour Le Havre et Cherbourg, mais une interpolation linéaire semblait hasardeuse, pour ne pas dire vouée à un éche certain. Ce point d'histoire n'a pas été totalement divulgué; l'interpolation a sans doute été faite "au feeling" au vu des terrains côtiers, des courants... et des quelques maigres observations nocturnes glanées lors de misions de reconnaissance à hauts risques.

Toujours est-il que le verdict tomba du cuivre des machines de Kelvin: 5, 6 ou 7 Juin! On sait que la météo du 5, très mauvaise, et l'espoir d'une légère amélioration, firent reporter la date du 5, choisie par Eisenhower, au 6.

Note demandant le calcul (d'après une image de l'article de B. Parker)

Pour Conclure...

Kelvin était, dès sa jeunesse, un grand admirateur de Fourier; il avait eu comme un coup de foudre pour son traité, qu'il avait découvert en 1839, à l'âge de 15 ans:

"J' étais rempli de la plus profonde admiration pour la splendeur et la poésie qui émanaient du livre de Fourier. [...]
Aussi, le 1^er Mai, le jour même où les prix furent remis, j'empruntais son ouvrage à la bibliothèque de l'Université et je le dévorais sans relâche; en une quinzaine, j'en maîtrisais la matière. "

Lord Kelvin

Aujourd'hui, les composantes principales de la marée dans un port quelconque peuvent être facilement repérées en analysant les données (hauteurs fonctions du temps) grâce à la... Transformation de Fourier. Celle-ci déterminera les fréquences essentielles (en abcisse sur le graphique ci-contre) qu'il sera facile d'identifier avec leurs habituels noms de code, et l'importance de leur contribution (en ordonnée) Tout se passe comme si chaque port laisse, par transformée de Fourier, son empreinte digitale!
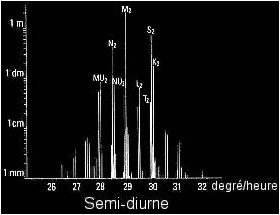Spectre de marée, image issue de cette page (de ce site)
D'autres spectres de marée sur le site de l'Ifremer

D'autres machines mécaniques plus ou moins similaires (pour les coefficients de Fourier)

Un premier exemple est une variante sur le principe (elle utilise une intégration par parties) de l'analyseur de Kelvin. Elle a été conçue par Olaus Henrici (1840-1918), présentée par lui-même (1894) ou décrite dans ce document (Dayton Miller in Journal of the Franklin Institute, vol 182, n°3 [1916], pp.285-322). Cette machine calcule 30 paires de coefficients, mais certains modèles pouvaient aller jusqu'à 100, ainsi celui de la DGA au Bassin des Carènes à Rouen (voir l'ouvrage d'E. Hébert dans les références ci-dessous).

Un second et fascinant exemple est une machine construite en 1897 par Albert Michelson (le célèbre physicien de l'expérience éponyme, démontrant l'invariance de la vitesse de la lumière): elle peut effectuer à elle-seule l'analyse et et la synthèse! Son fonctionnement est détaillé en détails dans cette excellente préesntation vidéo de Bill Hammack:

Elle est complétée par cette description.

Michelson a voulu éviter la sommation par le câble, qui entrainait trop d'erreurs si l'on augmentait le nombre de termes, d'une part, et produire les mouvements harmoniques de base en utilisant des ressorts, d'autre part. Cette première machine pouvait sommer 20 termes, ou calculer 20 coefficients de Fourier; mais fort de son succès, Michelson put obtenir les financements pour en construire une à 80 termes dès l'année suivante. Machine avec laquelle, grâce aux graphes tracés, il a peut-être pris conscience de ce que l'on appelle le phénomène de Gibbs.

Références Spécifiques à cette page

B. CASSELMAN, Fourier Analysis of Ocean Tides
B. CASSELMAN, JAVA animation of theTide Predicting Machine
M.-J. DURAND-RICHARD, Les Mathématiques comme Production Culturelle (diaporama , IREM Nantes 2008)
B. ESCUDIE, C. GAZANHES, H. TACHOIRE, V. TORRA, Des Cordes aux Ondelettes (Presses de l'Université de Provence)
C. GAZANHES, L'Analyse Harmonique, des Procédés Mécaniques aux Procédés Électroniques
B. HAMMACK, S. KRANZ, B. CARPENTER, Albert Michelson's Harmonic Analyzer (Articulate Noise Books)
E. HEBERT, Instruments Scientifiques à travers l'Histoire (Ellipses)
T. KÖRNER, Fourier Analysis (Cambridge University Press)
H. de MORIN, Les Appareils d'Intégration (Gauthier-Villars)
R. OTNES, Notes on Mechanical Fourier Analyzers
T. PHILIPS, Tides and Tide Prediction
P. SCHUREMAN, Manual of Harmonic Analysis and Prediction of Tides (U.S. Department of Commerce)
W. THOMSON (Lord KELVIN), Mathematical & Physical Papers, vol. 6 (Cambridge University Press), pp. 272-297
W. THOMSON, P. TAIT, Treatise on Natural Philosophy, vol. 1, part 1 (Cambridge University Press, 2^nd ed 1879), pp. 272-297
W. THOMSON, P. TAIT, Un Instrument pour le Calcul de l'Intégrale du produit de Deux Fonctions (Trad. M.-J. DURAND-RICHARD)
P. WOODWORTH, Tide Prediction Machines (Congrès SLOC, 21/06/2103)
P. ZETLER, The Evolution of Modern Tide Analysis and Prediction- Some Personal Memories (1987)

Site du SHOM: Prédictions en Ligne.
Site TIDES & CURRENTS: Machines à Prédire aux USA (bien documenté, avec photos)

Poursuivre...

Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes    (Prélude à la Théorie Analytique, #0.2)

Aller à la Page:    Naissance des Séries de Fourier       (Promenade dans la Théorie Analytique, #1)
Aller à la Page:    l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Aller à la Page: Naissance de la Transformée de Fourier    (Promenade dans la Théorie Analytique, #3)

Aller à la Page:    Naissance de la FFT: Fast and Fourier !     (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page:    Signaux, Transformées... et Applications         (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie...    (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page:     Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page:    Brève Histoire des Séries Trigonométriques   (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes          (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval        (Promenade dans... la suite de l'histoire, #6)

Aller à la Page:       du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page:     Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire      (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres       (e est irrationnel... sa VRAIE preuve !)
Aller à la Page:     Hommage à Jean-Pierre Kahane                                                                 (une vie pour Fourier...)

Revenir à la Home Page du Mathouriste