Harmonique, vous avez dit: Analyse Harmonique?

... Une Promenade Fouriériste! (Partie 0.3)

Si la musique qui nous a servi d'illustration était du XX^ème siècle, la physique et les mathématiques utilisées dataient indiscutablement du XIX^ème ... La merveilleuse simplicité de la méthode de séparation des variables de Fourier, l'élégance de la recherche des modes propres sont-elles encore d'actualité dans la science récente?
La réponse est oui... en trois exemples!
Notre vagabondage musical se pouruit donc à l'avant-garde de la Physique contemporaine.

Quelques Applications Modernes des Modes Propres et des Séries de Fourier...

Niveaux d'Énergie de l'Atome d'Hydrogène

La Mécanique Quantique est l'une des deux révolutions de la Physique du XXème siècle (l'autre étant, évidemment, la Relativité d'Einstein).

Pour présenter très brièvement le problème, le modèle planétaire de l'atome (Rutherford, 1911) offrait une contradiction, évidente dès le cas le plus simple, celui d'un électron gravitant autour d'un noyau d'hydrogène : la rotation de l'électron autour du noyau devait, du fait de sa charge électrique, engendrer une perte d'énergie par rayonnement, donc induire un mouvement en spirale, menant à une collision finale: aucun atome n'aurait pu être stable, et... nous n'aurions pas été là pour le remarquer! Elle fut résolue en 1913 par Niels Bohr , qui proposa l'existence d'orbites stationnaires (ou stables) où il n'y a plus cette perte d'énergie. Elles correspondent à des valeurs exceptionnelles, les niveaux d'énergie (on parle donc de quantification de l'énergie). Cet article fondateur est présenté et commenté sur BibNum, pour les lecteurs qu'un résumé de quelques lignes peut frustrer.

Le calcul de ces valeurs est l'un des premiers que rencontre l'étudiant lors de son initiation quantique. Et tout commence par l'application à l'équation de Schrödinger de la "bonne vieille" méthode de séparation des variables de Fourier!

À titre provisoire, le Mathouriste (qui entend placer ici un résumé des calculs plutôt que leur développement complet), vous propose ce petit document manuscrit, de sa main, détaillant cette application de la méthode de Fourier: vous y constaterez que cela continue de fonctionner sur le même schéma que les cas des cordes, des membranes, ... et bien sûr de la chaleur!

À la fin de cette première phase, il reste à résoudre l'équation différentielle obtenue. C'est plus long que difficile -en fait, accessible à un étudiant scientifique de niveau Bac+1: il n'aura à traiter que des équations à coefficients constants!

Pour n'en rien perdre, suivre pas à pas cet énoncé, directement inspiré de la bible du sujet:

C. COHEN-TANNOUDJI & alias, Mécanique Quantique, tome 1 (Hermann)

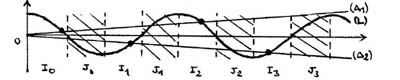
Si vous séchez, voici le corrigé.
Le point crucial, qui explique du point de vue mathématique la quantification, est que les diverses conditions à respecter aboutissent à déterminer, à deux reprises, les modes propres comme points d'intersection d'une sinusoïde et d'une droite de pente non nulle. Le caractère exceptionnel en est dès lors quasi évident.


Niveaux de première catégorie, solutions de: cos² α - α²/H = 0	Niveaux de première catégorie, solutions de: sin² α - α²/H = 0

Vous pouvez en complément voir aussi, dans notre page Fresnel, le paragraphe "Des Ondes Partout!" (petite visite en images à l'association scellée entre ondes et particules, qui présente l'irruption des ondes dans la physique des particules) et bien sûr "Fresnel et Fourier".

Chaos en Météorologie: le Système de Lorenz

Derrière les hommes politiques accusés de corruption et les médecins suspectés d'assasiner leurs malades, les prévisionnistes de la météo font une honorable troisième place sur le podium des gémonies ordinaires. Lorsque le Mathouriste était enfant, les caprices du climat étaient, vus du marché ou de la boulangerie, "la faute de ces fichus engins atomiques qui nous détraquent le temps". Depuis, on a progressé dans deux directions: la capacité de calcul des ordinateurs qui, reconnaissons le, a bien reculé l'horizon d'une prédiction assez fiable de trois jours à une, voire deux semaines, et la découverte d'une limite à l'arrogance triomphante de nos calculs: il faut beaucoup moins qu'une hideuse bombe A ou H; malheureusement, le plus charmant des papillons peut être la cause des catastrophes, ou, pour citer précisément par le titre de sa célèbre conférence, l'auteur du fameux paradigme, Edward N. Lorenz (1917-2008):

Fauteurs de troubles potentiels... ... dans la plus mathématique des collections du genre!	"Predictability : does the flap of a butterfly’s wings in Brazil set off a tornado in Texas ?" 139^th Annual Meeting of the American Association for the Advancement of Science (29/12/1972) (texte intégral)
	(texte intégral sur le site du Journal of Atmospheric Sciences)

Oui, il a fallu dix ans et un titre nettement plus accrocheur pour que l'article fasse enfin sensation dans le monde scientifique, puis que l'effet papillon ne devienne une expression courante, voire galvaudée. Mais quel mathématicien, quel physicien lisait le Journal of Atmospheric Sciences? Au fait, lisaient-ils seulement un de leurs plus éminents confrères?

"Pourquoi les mété́eorologistes ont-ils tant de peine à prédire le temps avec quelque certitude? Pourquoi les chutes de pluie, les tempêtes elles-mêmes nous semblent-elles arriver au hasard, de sorte que bien des gens trouvent tout naturel de prier pour avoir la pluie ou le beau temps, alors qu’ils jugeraient ridicule de demander une éclipse par une prière ? Nous voyons que les grandes perturbations se produisent généralement dans les régions où l’atmosphère est en équilibre instable. Les mété́orologistes voient bien que cet équilibre est instable, qu’un cyclone va naître quelque part ; mais où, ils sont hors d’état de le dire ; un dixième de degré en plus ou en moins en un point quelconque, le cyclone éclate ici et non pas là, et il étend ses ravages sur des contrées qu’il aurait épargnées. Si l’on avait connu ce dixième de degré , on aurait pu le savoir d’avance, mais les observations n’étaient ni assez serrées, ni assez précises, et c’est pour cela que tout semble dû à l’intervention du hasard."

H. Poincaré, Science et Méthode (1908)

Son buste, dans le Hall d'Honneur de l'École Polytechnique

Dix ans pour agiter un peu la communauté scientifique, et quinze de plus pour que le livre de James Gleick, La Theorie du Chaos (1987), fasse de Lorenz une star et mette l'effet papillon sur toutes les lèvres, avec un sens certain de la mise en scène, du décor (le MIT) et... de ce que était à son héros ce que l'Aston Martin est à James Bond:

"La machine, un Royal McBee, était un fouillis de fils et de tubes à vide peu esthétique qui occupait une partie du bureau de Lorenz; faisait un bruit insolite et irritant, et tombait en panne pratiquement chaque semaine. Elle n'eut jamais la vitesse et la mémoire suffisante pour simuler de façon réaliste l'atmosphère et les océans terrestres. Poiurtant, la météo miniature que Lorenz inventa en 1960 stupéfia ses collègues. Toutes les minutes, la machine indiquait l'écoulement d'une journée en alignant une rangée de chiffres sur une page de listing."

J. Gleick, La Theorie du Chaos

À ce stade, vous vous posez sûreùent la bonne question...

"Mais que vient faire l'Analyse de Fourier dans cette histoire? "

C'est là que Lorenz va plus loin que Poincaré, avec un calcul effectif. Mais c'est chez un prédécesseur peu connu, pour ainsi dire jamais cité par les (très nombreux) articles présentant celui de Lorenz, qu'il va chercher son point de départ. Et dans celui-ci, on découvre des séries de Fourier!

Météo: dificile, mais pourquoi?

Venu au Syndicat d'Initiative d'un village pyrénéen pour consulter, selon un sage principe de montagnard, les prévisions des jours à venir afin d'organiser ses randonnées, le Mathouriste put y lire cette nouvelle goguenardise:

"La météo est une science exacte... que Météo-France ne maîtrise pas complètement."

Tout modèle météorologique repose sur de méchantes équations aux dérivées partielles: les équations de Navier-Stokes (ou plus simplement ici, un survol assez convivial de l'essentiel), qui régissent les mouvements des fluides (liquides et gaz): les déplacements des masses d'air en relèvent donc. Leur différence essentielle avec celles des ondes ou de la chaleur, auxquelles la méthode de Fourier s'est appliquée avec succès, est leur non-linéarité; dès lors, le concept de superposition de solutions élémentaires ne s'applique plus. Pour ceux qui ne mesurent la difficulté qu'au montant de la rétribution, elles constituent le sixième des 7 problèmes du prix du millénaire offert par l'Institut de mathématiques Clay en 2000: leur tête a été mise à prix pour un million de dollars, à qui apportera une solution!

La prévision à l'échelle du globe avait commencé en 1855 sous l'impulsion de Le Verrier (voir notre page), qui avait compris que l'essor du télégraphe permettait d'obtenir instantanément des relevés en plusieurs points du globe. Une nouvelle étape décisive fut franchie en 1922 par Lewis Fry Richardson (1881-1953) qui publia Weather Prediction by Numerical Process, ouvrage qui définit les principes encore appliqués dans les modèles actuels: diviser la terre en "tranches" par méridiens et parallèles, et l'air au dessus selon plusieurs couches, formant ainsi des boîtes contigües comme autant de morceaux d'atmosphere dans lesquels les indicateurs météorologiques habituels: pression, température, vecteur vitesse du vent sont à peu près constants, et en tout cas supposés tels dans le modèle.


ensemble de cellules couvrant le globe terrestre (source: Interstices)	Cellules couvrant l'Europe (source: Luxorion)

Une version discrétisée des équations de Navier-Stokes (les dérivées deviennent des différences) permet de calculer, par un recours exclusif aux quatre opérations arithmértiques, l'évolution des valeurs du temps t au temps t +Δt, en fonction de l'état des cellules voisines. En théorie, rien de plus simple, mais en pratique, un nombre colossal d'opérations à effectuer, même avec un maillage relativement grossier; en particulier, il se limitait, verticalement, à 5 couches d'atmosphère (1 colonne = 5 cellules). Richardson a donné une évaluation intéressante dans son livre:

"Cela m'a pris le plus gros de six semaines de travail pour préparer les formulaires de calcul et déterminer une première fois la nouvelle distribution des valeurs dans deux colonnes. Avec l'habitude, un calculateur¹ moyen pourrait peut-être aller dix fois plus vite. Pour un pas de temps de 3 heures, il faudrait 32 individus pour effectuer le calcul en deux points, au même rythme que l'évolution réeelle. [...] Avec un quadrillage au sol défini par des divisions de 200km en 200km, la surface du globe serait couverte par 3200 colonnes. Le temps dans les tropiques est souvent bien connu à l'avance; on pourrait donc se contenter de 2000 colonnes. Il faudrait donc 32 x 2000 = 64000 calculateurs pour faire une prévision météorologique à l'échelle du globe. C'est une valeur atterrante. [...] Peut-être sera-t-il possible, dans quelques années, de simplifier ce processus."

L. Richarson, Weather Prediction by Numerical Process (1922)

Projet de quadrillage de l'Europe de l'Ouest,
donné par Richarson dans son livre Il envisageait "au dessus" cinq couches d'atmosphère.

1. Il s'agit évidemment d'un calculateur humain!

"Ce schéma de travail est compliqué parce que l'atmosphère est compliquée. Mais il a été réduit à un ensemble de formulaires de calcul. [...] Peut-être qu'un jour, dans un avenir imprécis, il sera possible d'effectuer les calculs plus rapidement que l'évolution des conditions météorologiques, et pour un coût moindre que celui que cette connaissance fera économiser à l'humanité. Mais c'est là un rêve."

L. Richarson, préface de
Weather Prediction by Numerical Process (1922)

ci-contre: un Cray-2 ayant appartenu à la Météorologie Nationale
(Paris, Musée des Arts & Métiers)

Météo: de Saltzman à Lorenz...

Il faut attendre le cinquième paragraphe de son texte (il en comporte 8, dont introduction et conclusion), pour qu'après des généralités plutôt abstraites, Lorenz se décide à présenter sa source d' inspiration:

"Dans cette section, nous introduisons un système de trois équations différentielles ordinaires dont les solutions présentent l'exemple le plus simple, à la connaissance de l'auteur, d'un flot déterministe non périodique. Ce système est une simplification de celui qu'a obtenu Salzman (1962) pour étudier la convection. [...]
Rayleigh (1916) a étudié le flot dans une couche de fluide de profondeur H, l'écart de température étant maintenu constant entre la surface supérieure et la surface inférieure. Ce système posède une solution d'équilibre, dans laquelle il n'y a aucun mouvement, et dans laquelle la température varie linéairement avec la profondeur. Si cette solution est instable, la convection peut se développer."

E. Lorenz, Deterministic Nonperiodic Flow

Source de l'image: site du documentaire de Josh Kastorf, The Real Lorenz

On peut d'emblée remarquer une différence importante entre les deux articles: alors que Saltzman cite 4 fois le nom de Fourier dès son préambule, Lorenz n'y fera quune petite allusion à la dérobée, en résumant le travail de Saltzman! Certes, le sujet n'est pas le même, et Lorenz part du point où Saltzman s'arrête, en quelque sorte.

L'article de Saltzman est, lui aussi intégralement disponible; nous en présentons ci-dessous les passages cruciaux où intervient l'analyse de Fourier.

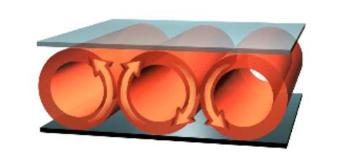
Saltzman commence par écrire les équations générales du fluide en mouvement: les fonctions inconnues sont:

(u,v,w) , coomposantes de la vitesse d'un point;
P, pression au point;
T₁, température au point.

Les variables sont x, y, z, coordonnées du point, et le temps t.
Les cercles rouges indiquent les non-linéarités.

Une simplification importante est de considérer qu'il n'y a aucun mouvement selon la coordonnée y: il n'est plus nécessaire de faire figurer ni y, ni la composante v dans cette direction, et le problème est réduit à deux coordonnées d'espace. Cela correspond à l'étude classique de rouleaux de convection (voir figure ci-dessus; y va d'avant en arrière), dite de Rayleigh-Bénard. Cest le phénomène évoqué plus haut avec Lorenz, et dont Saltzman situe la généralité dès la première phrase de son article:

" Á très peu d'exceptions près, les mouvements de l'atmosphère, à toutes les échelles, sont d'origine convective. Les causes premières des mouvements des masses d'air sont les inégalités thermiques que subit en permanence l'atmosphère soumise au rayonnement solaire. Les formes particulières que prennent ces mouvements varient énormément en échelle comme en caractère, allant de la turbulence chaotique à des systèmes hautement organisés comme les ouragans. Dans tous les cas, ils ont la propriété commune de transporter de la chaleur et de la vorticité, et ces processus sont responsables de la non-linarité du comportement de l'atmosphère. "

L'absence de y et v rend son équation de divergence (10) particulièrement agréable, car elle exprime que le champ (-u,v) dérive d'un potentiel scalaire qu'il introduit sous le nom de ψ .

	Cela lui permet, en éliminant la pression entre (7) et (8), de ne plus avoir que deux équations au lieu du groupe de quatre (7)-(10), avec deux fonctions inconnues, ψ et θ qui est une légère modification de T₁, Au vu de quoi, un diplômé de master de mathématiques, baignant dans les équations différentielles avec la même délectation que Bugs Bunny dans la Rhapsodie Hongroise n°2 de Franz Liszt, devrait avoir une réaction proche de celle de notre lapin préféré... au moment où il tourne la page! ( voir le dessin animé complet... pourquoi se priver de ce plaisir?)

Devant une difficulté clairement inhumaine... il faut ruser! La recherche de rouleaux de convection, traduits par des courbes fermées en x et z, pousse à l'emploi d'un développement périodique en chacune de ces coordonnées. Saltzman dégaine donc l'arme abolue:

Les formules sont certes un peu grosses, mais, en les décortiquant d'un peu plus près, elles n'ont rien de vraiment effrayant.

Les diverses * ne font que traduire des changements de variable simples visant à ne manipuler que des quantités adimensionnées.
Une fonction de deux variables φ (x,z) se développera en une série double au lieu d'une série simple, de fonctions

a_m,n exp (imx/L).exp (inz/H)

la forme exponentielle est bien plus simple, au moins pour la théorie, que celle qui utiliserait sinus et cosinus, et on ne se prive pas d'utiliser la propriété fonctionnelle

a_m,n exp (imx/L + inz/H)

les coefficients de Fourier s'expriment alors par des intégrales doubles analogues; pour chaque variable l'intégration porte sur un intervalle de longueur une période.
enfin, s'il y a une variable de plus, le temps t, pour chaque t fixé la fonction φ (x, z, t) se développera comme ci-dessus, avec des coefficients qui changeront avec chaque valeur de t, donc seront des fonctions de t.
a_m,n (t).exp (imx/L + inz/H)

Ces belles séries peuvent donc être reportées dans les équations, Lorenz résume fort bien la suite du calcul, au demeurant plus volumiseuse que difficile:

"Saltzman a obtenu un ensemble d'équations différentielles ordinaires en développant ψ et θ en séries de Fourier doubles de x et z, et en les substituant dans les équations. Il a mis chacune sous la forme d'une série de Fourier double, en remplaçant les produits de fonctions trigonométriques de x et z par des sommes de telles fonctions, et a identifié les coefficients d'une même fonction trigonométrique. Obtenant ainsi un système infini, il l'a réduit à un système fini en le tronquant à un ordre qu'il a choisi."

E. Lorenz, Deterministic Nonperiodic Flow

Les dérivations par rapport au temps sont uniquement du premier ordre dans le système dans (16), (17). Par suite, les seules dérivées par rapport au temps qui figureront seront des a'_m,n (t). Par ailleurs, les termes non linéaires induiront des produits de deux termes, qui laisseront leur trace dans des produits de deux coefficients, mais rien de plus "méchant". Ce qui permet à Saltzman de prédire la forme (ci-contre) du système différentiel ordinaire qu'il obtient, avec pour seule variable t.

La troncature le laisse tout de même avec... 52 équations!

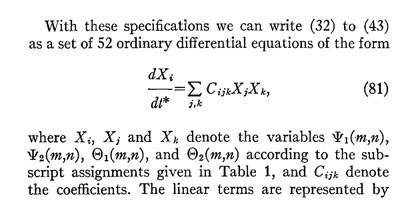Avait-on le droit de dériver terme à terme? D'identifier?
Quiconque a fait un peu de mathématiques sait qu'on ne manipule pas les sommes infinies comme les sommes finies. MAIS

Puisqu'on va tronquer, la question est assez byzantine! Ôtons d'abord tous les termes qui n'interviendront pas dans le résultat du calcul formellement effectué par Saltzman, c'est à dire, tronquons a priori "assez loin": les mêmes calculs portent sur une somme finie, il n'y a plus aucun manque de rigueur!
Tronquer fournit-il encore un système représentatif? Voilà belle lurette que les astronomes le font et que cela donne de bons résultats! Sans doute faut-il garder l'esprit vigilant, et se tenir prêt à réintroduire un terme abusivement négligé... Le procédé reste inévitable pour les calculs pratiques; il se contrôlera en reconfrontant a posteriori les prévisions obtenus d'une part à la réalité observée, mais aussi à un modèle tronqué "plus loin" pour mesurer au moins l'influence des premiers termes négligés.
Concernant la météo, on peut induire que si un système simple, avec peu de termes, met en évidence de l'imprévisibilité, ce sera a fortiori vrai pour un système plus compliqué!

Saltzman donne un peu plus loin un exemple encore plus réduit, à 7 fonctions inconnues seulement, et met en évidence numériquement une instabilité. Lorenz quant à lui, tire profit des résultats de son prédécesseur pour se limiter à 3 fonctions seulement, les autres s'avérant assez proches de zéro après le calcul numérique de Saltzman. Voici comment Ian Stewart résume le passage de l'un à l'autre; il est l'un des rares vulgarisateurs à ne pas faire une injuste impasse sur Saltzman... mais saurez-vous repéréer l'endroit où, à mots couverts, il fait allusion aux séries de Fourier?

" Sur un mode typique des mathématiques appliquées classiques, Saltzman devina une forme approximative de la solution, il la substitua dans ses équations, négligea quelques termes bizarres mais petits, et jeta un coup d'æil au résultat. Même ses équations tronquées étaient trop difficiles à résoudre par une formule, il les mit donc dans un ordinateur.
Il remarqua que la solution semblait subir des fluctuations irrégulières: une convection irrégulière. Mais elle n'avait pas du tout l'air périodique.
Lorenz était intéressé et décida d'en savoir plus. Observant que seules trois des variables de Saltzman jouaient un rôle dans cet effet, Lorenz se débarassa des autres. C'était un acte hautement désinvolte mais parfaitement conscient. Il obtint un système d'équations qui est maintenant devenu classsique."

I; Stewart, Dieu joue-t-il aux dés?

La limitation à la dimension 3 permettra la fantastique visualisation qui contribuera largement à son succès... bien sûr, il ne le sait pas encore! Voici ces deux systèmes: observons que Lorenz opte pour une troncature a priori (cf rem. 1 ci-dessus), ce qui allège bien le calcul; les deux termes non linéaires qui demeurent dans son système ont été encerclés, il y en a bien davantage (treize) dans celui de Saltzman.

SALTZMAN	LORENZ

La suite est bien connue; elle a été racontée de nombreuses fois, vous la retrouverez en détails dans les ouvrages donnés ci-dessous en référence. Le calcul repris "à mi-course", pour gagner du temps et aller plus loin, la réintroduction manuelle des valeurs de l'état affiché du système à ce moment là, et la divergence rapide avec la partie connue du calcul précédent, poursuivi à partir de l'état calculé. L'état affiché n'en différait que de façon infime, par l'effet d'arrondi à l'affichage; ainsi se trouvait mise en évidence la sensibilité aux conditions initiales. Les séries de Fourier étaient déjà bien loin en arrière...


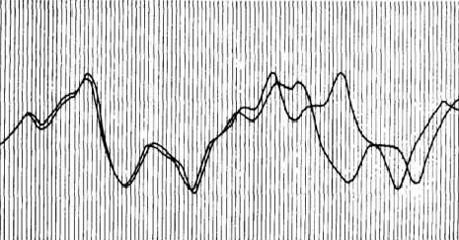
graphique d'une des coordonnées du système de Lorenz: départ en deux points très proches, divergence au bout d'un temps fini assez bref.	Image de Paul Bouke à voir (ave bien d'autres) dans cette page

La meilleure façon de poursuivre en images animées de qualité, c'est LE film d'Etienne Ghys et Jos Leys : CHAOS, Une aventure mathématique; 9 chapitres de 13' chacun, pour tous publics!
En particulier, le chapitre consacré à l'attracteur de Lorenz; vous pouvez d'ailleurs le voir directement, sans passer par les chapitres précédents (que vous ne manquerez pas de visionner par ailleurs, vous perdriez quelque chose à vous en priver!)


d'après la page d'accueil du film et sa bande annonce	sur la page du chapitre

Météo: et Aujourd'hui?

Tout d'abord, pour un panorama de présentation, nous vous conseillons ce diaporama de présentation des méthodes actuelles, qui n'oublie d'ailleurs pas l'histoire de la prévision. Il a été conçu à l'École Nationale de la Météorologie, difficile d'avoir une meilleure référence. Nous en extrayons deux faits saillants parmi beaucoup d'informations intéressantes:

L'évolution des calculateurs (cette fois, il s'agit des machines!) a permis de passer du modèle de Richardson (5 couches et points du maillage distants de 200km, écarts temporels de 3h) à des modèles comme ARPEGE, de Météo-France: 105 niveaux verticaux de 10m, des points de maillage distants de 7,5km en France, 36km aux antipodes, un pas de temps de 6'!
Une nouvelle méthode, la méthode spectrale, se substitue au calcul des différences finies, approximation discrète du calcul des dérivées (remplaçant les équations différentielles par des sytèmes algébriques). Petit rappel: c'est pour ce type de traitement que Babbage avait inventé ses machines à différences... voir notre page!

Mais quest-ce que la méthode spectrale? Pour le dire en peu de mots, une décomposition des fonctins inconnues du système de Navier-Stokes en séries de fonctions orthogonales, sinusoïdes (cas initial de Fourier) ou fonctions plus générales, comme les harmoniques sphériques, particulièrement bien adaptées à la géométrie du globe et de son atmosphère. Ces fonctions particulières ont été introduites par Legendre pour son étude du potentiel, mais l'idée générale des développements orthogonaux est celle qui tisse le fil conducteur du traité de Fourier (voir nos pages d'étude du traité, particulièrement celle-ci) et qui constitue le succès éclatant de sa méthode dans les problèmes physiques.
Aujourd'hui donc, plus que jamais, la météo, c'est du Fourier, encore du Fourier, toujours du Fourier!

En tout cas, ne ratez pas ce prétexte pour déguster un Weather Report grande époque!

Au hasard, un Birdland live...
... ou mieux encore, live toujours, mais avec LA rencontre surprise: on ajoute le groupe qui en a fait une mythique version vocale, Manhattan Transfer... quand on vous dit que la prévision est difficile!

Références pour ce Paragraphe

Pour s'initier...

E. GHYS, L’Effet Papillon sur le site Image des Maths (CNRS)
E. GHYS, J. LEYS, CHAOS, Une aventure mathématique; film en 9 épisodes.( les chapitres 7 et 8 vous parlent de Lorenz)
J. GLEICK, La Theorie du Chaos (Champs-Flammarion)
I. STEWART, Dieu joue-t-il aux dés? (Champs-Flammarion)
A. DAHAN-DALMEDICO, J.-L. CHABERT, K. CHEMLA & alias, Chaos et Déterminisme (Champs-Flammarion)

Pour aller un peu plus loin...

K. ALLIGOOD, T. SAUER, J. YORKE , Chaos, an Introduction to Dynamical Systems (Springer)
E. GHYS, L’attracteur de Lorenz, Paradigme du Chaos
E. GHYS, The butterfly effect (12ème Congès sur l'Éducation Mathématique, Séoul 2012)
M. KREITZ, Prévoir le temps, Météo à l'École ('École Nationale de la Météorologie / Météo-France, Toulouse)
H.-O. PEITGEN, H.JÜRGENS, D. SAUPE, Chaos and Fractals: New Frontiers of Science (Springer)
P. LYNCH, The Emergence of Numerical Weather Prediction, Richardson's Dream (Cambridge)
F. VERHULST, Nonlinear Differential Equations and Dynamical Systems (Springer)
L.F. RICHARDSON, Weather Prediction by Numerical Process (Cambridge)
M. VIANA, What’s new on Lorenz strange attractors ? (Math. Intelligencer, 22, n^o. 3, 2000)

Système Solaire, Héliosismologie, Exoplanètes, Ondes Gravitationnelles

Vous brûlez d'en savoir plus sur les succès de la Transformée de Fourier dans l'espace au XXI^ème siècle?
des atmosphères des planète sde notre brave système solaire aux exoplanètes, des galaxies aux trous noirs?

Vite, n'attendez plus! Consultez nos pages dédiées (afin de ne pas augmenter démesurément le volume de celle-ci)

Fourier, Vénus, Mars et les Autres : au service de l'Astrophysique, de 1977 à... l'actualité la plus récente.;
Fourier et les Exoplanètes : au service de la méthode des vitesses radiales;
Fourier et les Ondes Gravitationnelles grâce à une géniale généralisation, la théorie des Ondelettes.

Poursuivre...

Revenir à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Revenir à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)

Aller à la Page:    Naissance des Séries de Fourier       (Promenade dans la Théorie Analytique, #1)
Aller à la Page:    l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Aller à la Page:    Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)

Aller à la Page:    Naissance de la FFT: Fast and Fourier !     (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page:    Signaux, Transformées... et Applications       (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page:     Cristallographie, Optique, Spectroscopie...    (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page:     Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page:      Brève Histoire des Séries Trigonométriques   (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page:    De Gabor aux Ondelettes        (Promenade dans... la suite de l'histoire, #5)
Aller à la Page:    De Pythagore à Parseval          (Promenade dans... la suite de l'histoire, #6)

Aller à la Page:       du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page:     Kelvin, l'Analyse de Fourier et les Marées     (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page:     Fourier, père de l'Optimisation Linéaire      (Promenade dansles sommets... avec Giacometti!)
Aller à la Page:     Fourier, Théoricien des Nombres       (e est irrationnel... sa VRAIE preuve !)
Aller à la Page:     Hommage à Jean-Pierre Kahane                                                                 (une vie pour Fourier...)

Revenir à la Page Biographique

Revenir à la Home Page du Mathouriste