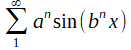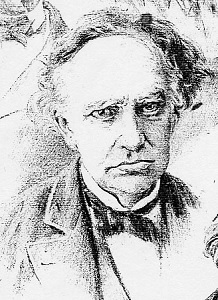Une Brève Histoire des Séries Trigonométriques ...
... Une Promenade Fouriériste! (Partie 4.4)
Le Mathouriste vous propose ici une petite promenade dans le temps, pour faire voir la richesse, la variété et... la difficulté! des questions soulevées par le travail de Fourier, tout le temps qu'il a fallu pour les résoudre, et l'immense chamboulement des Mathématiques qui s'en est suivi. Un chantier qu'on pourrait comparer, pour qui n'a pas fréquenté ces chapitres de mathématiques (c'est à dire, une très grande partie de la population... donc, chères lectrices et cherslecteurs, pas de complexes déplacés), au bouleversement qu'a fait subir Hausmann à la ville de Paris!. D'autres de nos pages sont dévolues aux applications: on n'évoque donc ici que les retombées internes à la discipline, et, autant que possible, sans trop de technicité.
Il s'agira surtout de l'après Fourier, mais, pour le lecteur qui rentrerait par cette porte, on mentionnera quelques liens et repères.
Calendrier de l'Avent
- Entre 100 et 200... Considérée d'un point de vue géométrique, l'utilisation des séries trigonométriques remonte à l'Antiquité grecque, dont la Compositione Mathématique de Ptolémée (~100-~170) contitue triomphalement la synthèse, la mise en ordre, l'achèvement: les astronomes musulmans ne s'y sont pas trompés, qui lui ont laissé le nom mieux connu d'Almageste ("La très grande", en Arabe).
z = R1 eiω1t + R2 eiω2t
ou, si l'on est plus habitué aux coordonnées réelles:x = R cos ω1t + R2 cos ω2t
y = R1 sin ω1t + R2 sin ω2t
y = R1 sin ω1t + R2 sin ω2t
Rien n'empêche de continuer, en disposant un troisième cercle centré sur le deuxième, ce qui revient à introduire un troisième terme dans les expressions des coordonnées; de fait, certains astronomes postérieurs l'on fait, pour améliorer la précision du modèle. Car s'il est mécaniquement faux (on sait maintenant qu'il n'en est pas ainsi), le modèle est prédictif, donc scientifique (il permet de calculer les positions futures) et d'une grande rigueur au sens de l'approximation mathématique: que la trajectoire soit une ellipse képlérienne (modèle où le soeleil est vu "seul" avec la planète étudiée), ou plus compliquée si l'on tient compte des perturbations dues à l'attraction d'autres astres (voir comment Le Verrier a découvert Neptune), tant que cette trajectoire est régulière (possède en tout point une tangente qui varie sans à coups), le théorème de Dirichlet, qu'on évoquera plus bas, montre que l'on peut réaliser une approximation à n'importe qu'elle précision par la série de Fourier. Les méthodes de l'astronomie grecque constituent donc une approche empirique de cette théorie.
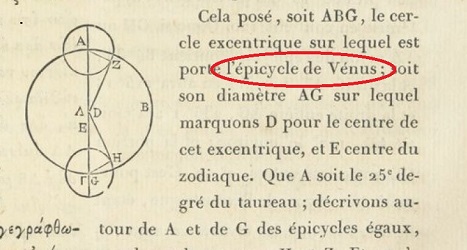 Mouvement de Vénus sur un épicycle, dans l'Almageste |
 Mouvement de Saturne sur un épicycle, dans l'Almageste |
|
" [...] Hipparque, l'homme le plus passionné pour la vérité, n'a recherché que les hypothèses du soleil et de la lune, en
prouvant qu'il était possible de rendre absolument compte de leur
révolution par des combinaisons de leurs révolutions par des
combinaisons de mouvements circulaires et uniformes ; tandis que pour les cinq planètes, dans les mémoires qu'il nous a maissés, il n'a même pas abordé kla question [...]"
C. PTOLÉMÉE, Compositione Mathématique, IX.2
|
|
Ainsi Ptolémée signale t-il que, s'il est le premier à employer les épicycles pour le mouvement des planètes, Hipparque les connaissait déjà; et il faut probablement en faire remonter l'invention à unée époque antérieure:
|
"Quelques grands, en effet, que
soient les services rendus par Hipparque à la science, son rôle me
paraît avoir été singulièrement exagéré. C'est aux astronomes
antérieurs de l'École d'Alexandrie, et en particulier à Apollonius de Pergé que doivent, à mon avis, être restituées l'invention des méthodes géométriques et trigonométriques [...] ."
P. TANNERY, Recherches sur l'Histoire de l'Astronomie Ancienne
|
- Entre 1200 et 1600... On retrouvera cette technique d'approximation efficace chez les astronomes musulmans, notamment Al-Tusi à l'Observatoire de Maragheh, mais aussi, plus surprenant peut-être, au moins si l'on se réfère, non à ce qui en est dit couramment, mais à ce qui n'en est presque jamais dit... dans le De Revolutionibus de Copernic: remettre en cause la position relative du Soleil et de la Terre, c'est une chose; abandonner la théorie des épicycles, c'en est une autre... il faudra attendre Képler et ses ellipses!
- Entre 1700 et 1800.. Du point de vue analytique, cest encore l'Astronomie qui mettra les séries de Fourier à l'honneur, avec la théorie de la lune de Clairaut (1745). Pour étudier une équation différentielle à cœfficients constants, mais avec un second membre "compliqué" (échappant aux cas usuellement calculables)
U "(θ) + U(θ) = 1 + Ω(θ)
il a l'idée de le remplacer par un développement en série trigonométrique, pour se ramener par somme au cas élémentaire d'un second membre en sinus ou cosinus.
Sur les sujets de ce paragraphe, vous trouverez un peu plus de précisions mathématiques dans ce petit article écrit par votre serviteur.
Et Fourier créa la Série...
Juste avant Fourier... c'est bien sûr la célèbre Controverse des Cordes Vibrantes. Sa place pourrait (devrait ?) être dans le paragraphe précédent, mais puisque nous cela fait partie de nos pages d'initiation à la théorie de Fourier, allez la découvrir dans notre page d'initiation musicale, en compagnie de quelques virtuoses de la Gibson, pour un plaisir maximum!À ce moment de l'histoire, c'est là qu'il aurait été naturel de creuser le sujet des séries trigonométriques. Personne ne semble y avoir pensé... de sorte que Fourier l'introduit sur la question de la chaleur (voir notre page), pour lequel la décomposition en modes propres est physiquement bien moins naturelle, quoique mathématiquement-c'est à dire abstraitement!- tout aussi pertinente. Fourier n'est pas pour rien le fondateur de la Physique Mathématique!
Fourier for Ever: Il n'y a plus d'Après?
La Convergence
- 1807, 1811, 1822: le point de vue de Fourier.
| "En général, les séries auxquelles nous sommes parvenus, en développant les diverses fonctions, sont toujours convergentes; mais il ne nous a point paru nécessaire de le démontrer ici: car les termes qui composent ces suites ne sont que les coefficients des termes qui donnent les valeurs des températures; et ces coefficients affectent des quantités exponentielles, qui décroisseent très rapidement, en sorte que ces dernières séries sont très convergentes. "
Fourier, Théorie Analytique de
la Chaleur, ch III, § 228 ( 1822)
|
Et tâchons de le comprendre un peu mieux que Poisson et Lagrange:
- la convergence de sa série n'est pas son objet d'étudie! Ce n'est qu'un problème marginal, au sens propre du terme: cela concerne un bord du domaine
ESPACE × TEMPS. Il a besoin des coefficients, non pou
reconstruire la fonction de départ, mais pour obtenir la solution de
l'équation de la chaleur à l'intérieur du domaine.
- Et là, non seulement il y est attentif "en théorie" (la présence des exponentielles en fait une évidence puisque les coofficients sont bornés pour toutes les fonctions quil peut considérer), mais aussi en pratique: il suffit, nous dit-il plus loin, de quelques termes seulement -guère plus de 3, le plus souvent) pour avoir une excellente approximation: c'est le sens à donner à l'expression, qui peut surpendre aujourd'hui, mais qui est pleine de bon sens. Le résultat est correct, et en accord avec l'expérience. Que demander de plus?
- 1829: La première preuve rigoureuse!

Elle est donnée par l'allemand Gustav Lejeune-Dirichlet (1805-1859) , dont la famille par alliance ne vous sera pas inconnue: il avait épousé Rebecca, la plus jeune sœur de Felix Mendelssohn. De 1822 à 1826, il avait étudié en Sorbonne à Paris, et il avait eu l'occasion de côtoyer Fourier. On ne s'étonnera donc pas que l'article soit rédigé en Français. On peut le lire ici.
Quoique'il commence par dire, comme Fourier, que ces séries " jouissent entre autre propriétés remarquables de celle d'être convergentes", il va introduire des hypothèse un peu plus restrictives, en théorie au moins, puisqu'elles seront vérifiées sur tous les exemples considérés... jusque là!
Mais d'abord... il va se payer Cauchy: l'apôtre de la rigueur a commis, dans sa tentative de preuve, une hénaurme faute, du genre à faire rugir un prof de prépa: il a affirmé que deux séries équivalentes (les termes génraux ont un rapport de limite 1) sont de même nature. Or, ce n'est vrai que pour les séries de signe constant, et Dirichlet lui assène le contrre-exemple maintrnant célèbre, et donné depuis dans tous les cours: qu'il commence par balayer devant sa porte!
Après quoi il entreprend sa démonstration, pratiquement telle qu'on la donne aujourd'hui: rassembler la somme partielle de rang n sous la forme d'une seule intégrale, faisant apparaître le noyau de Dirichlet:
sin (nt) / sin t



Ou, pour laisser à Riemann le soin de le dire, dans un texte qu'on évoquera un peu plus loin:
|
"En effet, pour tous les cas de la nature, les seuls dont il d'agit ici, la question était complètement résolue;
car si peu que nous sachions comment les forces et les états de la
matière varient avec le lieu et avec le temps dans les infiniment
petits, nous pouvons cependant admettre en toute sécurité que les fonctions auxquelles ne s'appliqueraient pas les recherches de Dirichlet ne se rencontrent pas dans la nature."
B. RIEMANN, op.cit.
|
- 1873: Le premier accroc!
| Qu'en est-il pour une fonction qui ne serait que continue? Dans l'ensemble, les mathématiciens croient à un résultat positif. Bernhard, frère Bernhard, ne vois-tu rien venir? Hélas, l'intéressé se morfond!
Mais quand arrive une réponse sous la plume de Paul Du Bois-Reymond (1831-1889), la surprise est de taille: il a réussi à construire une fonction continue pour qui la série de Fourier diverge en un point. (Son article, en Allemand). C'est évidemment un exemple construit ad hoc: l'auteur lui a doonné une infinité de fortes oscillations au voisinage de 0. Très loin déjà des braves et honnêtes fonctions rencontrées en pratique... |
 |
|
- 1966: ENFIN tout savoir sur le cas des fonctions continues!
 |
Cela pouvait-il être plus grave? L'ensemble de divergence pouvait-il être "grand"? Il a fallu presqu'un siècle pour en venir à bout! Lennart Carleson (né en 1928) a établi en 1966 que, pour une fonction continue, l'ensemble des points de divergence est de mesure nulle. (Sommairement: pour tout ε>0, l'ensemble peut être enfermé dans une réunion d'intervalles ouverts dont la longueur, s'ils étaient mis bout à bout, n'excèderait pas ε: cette notion a pour cadre la théorie de l'intégrale de Lebesgue, dont on parlera plus loin). Un dégât somme toute limité, si l'on pense qu'Andreï Kolmogorov (1903-1987) avait réussi a construire en 1926 une fonction intégrable (au sens de Lebesgue) dont la série de Fourier diverge partout! L'article de Carleson est réputé très difficile: on peut en lire la présentation de Jean-Pierre Kahane au Séminaire Bourbaki. Il a obtenu le Prix Abel en 2006, et le communiqué de presse (montage d'extraits ci-contre), qui rend hommage à son travail, ne manque pas de commencer par saluer celui de Fourier. Il souligne la double surprise que constitue la résistance inattendue du problème et sa solution à un moment où l'on ne l'attendait pas. Lire aussi une interview de Carleson. |
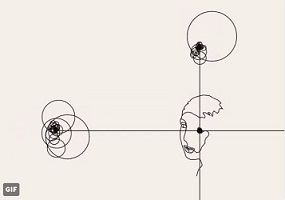
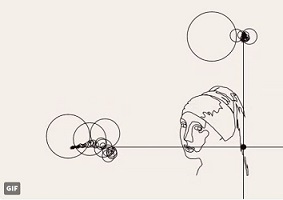
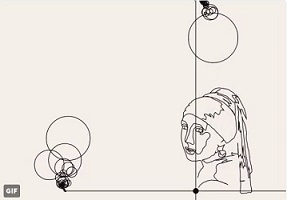
Récréation: tout ce qu'on peut faire avec le théorème de Dirichlet!En Février 2018 est apparue sur
la toile une vidéo assez spectaculaire: on y voit un crayon dessiner
d'un seul trait, à partir de deux "mystérieux" mouvements circulaires
combinés, l'un en abcisse, l'autre en ordonnée, la Jeune fille à la Perle de Vermeer de Delft.
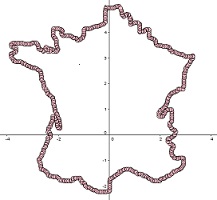
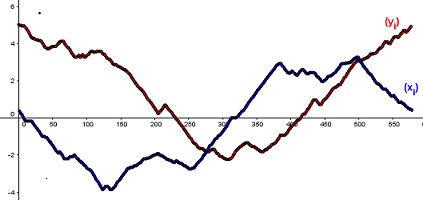
Sur sa lancée, Choux, etc... nous propose un autre exemple, tout aussi propre à surprendre le visiteur non averti, tout aussi justiciable du théorème de Dirchlet : un tracé d'une carte de France. L'envers du décor est ainsi révélé: grâce à une (patiente et courageuse) numérisation de 578 points, on peut déployer abcisse et ordonnée pour mieux visualiser ces fonctions, et faire un calcul approché, par transformée de Fourier discrète, des coefficients de Fourier: on possède alors tout ce dont on a besoin pour l'opération inverse. Et ça marche bien, et c'est normal: la France a un bord de classe C1, comme on dit, ou mieux C1 par morceaux, car, tout de même, il ne faut pas exagérer: le fond de l'estuaire de la Gironde, la presqu'île de Crozon, le Cap Gris-Nez ou la pointe de la frontière Nord-Est du côté de Strasbourg ont l'allure d'aspérités avec deux demi-tangentes différentes à droite et à gauche... Une remarque...
Et voilà qui nous permet de poser une intéressante question subsidiaire: cela marchera-t-il pour tout pays? |
|||||||||||||||
 |
 Voir l'article complet (l'emploi des séries de Fourier est mis en évidence) |
|
| Maison natale de Von Neumann et sa plaque commémorative, à Budapest (Hongrie) |
||
|
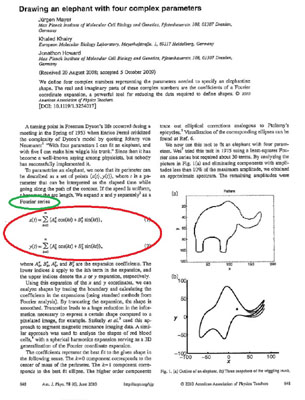
Von Neumann voulait seulement signifier qu'à force de rajouter des
paramètres à un modèle, on peut lui faire prédire tout ce qu'on veut.
Mais un chimiste a tenté, en 1975, et trois biologistes ont réussi, en
2009, à relever le gant en publiant un article sur le sujet. Jusqu'au mouvement de trompe de l'éléphant!
Pour ce faire, un développement de Fourier à une trentaine de termes a été filtré (c'est un des principes de compression - voir notre page dédiée ) en ne retenant que les 4 (ou 5) composantes qui ont le plus grand coefficient.
|
||
La Mauvaise Réputation
Jean-Pierre Kahane a pu titrer à bon droit un paragraphe "Les Séries Trigonométriques comme Sujet peu Recommandable" dans l'ouvrage co-éctrit avec P.-G. Lemarié, Séries de Fourier et Ondelettes. Avant même l'irruption de la fonction de Du Bois Reymond, Riemann avait semé le trouble. Une première fois dans son mémoire de 1854 (voir ci-dessous), en y introduisant une série "exotique":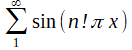
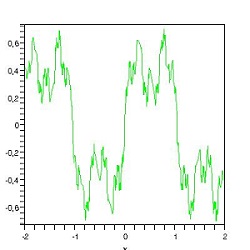
De la deuxième fois, il n'y a hélas pas de trace écrite. Weierstrass rapporte que Riemann, qui croyait à l'existence de fonctions continues mais nulle part dérivable, aurait proposé à ses étudiants l'exemple
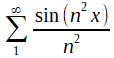
m Stèle à Jean Perrin
(Paris, Rond-Point des Champs Elysées) |
"Si
les fonctions à dérivée sont les plus simples, les plus faciles à
traiter, elles sont pourtant l'exception; ou, si l'on préfère un
langage géométrique, les courbes qui
n'ont pas de tangente sont la règle, et les courbes bien régulières,
telles que le cercle, sont des cas fort intéressants, masis très
particuliers.
Au premier abord, de telles restrictions semblent n'être qu'un exercice intellectuel, ingénieux sans doute, mais en définitive artificiel et stérile, om se trouve poussé jusqu'à la manie le désir d'une rigueur parfaite. Et le plus souvent, ceux auxquels on parle de courbes sans tangentes ou de fonctions sans dérivées commencent par penser qu'évidemment la nature ne présente pas de telles complications et n'en suggère pas l'idée. C'est pourtant le contraire qui est vrai, et la logique des mathématiciens les a maintenus plus près du réeel que ne faisaient les représentations pratiques employées par les physiciens. " J. PERRIN, Les Atomes (1913)
|
le médaillon; l'inscription gravée aurait bien besoin d'être repeinte!
|
La Sérénité Retrouvée
- 1900: Fejér: Le hongrois Lipót Fejér (1880 – 1959) ramène la confiance après la "bombe" de Du Bois-Reymond. Si, pour une fonction continue, les sommes partielles de Fourier peuvent diverger, leur moyenne arithmétique converge toujours. Des notes de devoirs surveillés aux vicissitudes boursières, tout un chacun peut comprendre que la moyenne a un effet régulateur, apaisant, gommant les accidents et bizarrerieLa première publication est en Français, comme le veut l'époque... c'est une note assez brève aux Comptes-rendus de l'Académie des Sciences, qui commence par un rappel du théorème d'Ernesto Cesàro (si une suite admet une limite l, la suite des moyennes arithmétiques converge aussi vers l) et se poursuit en montrant qu'au sens de la moyenne, la série cos(nx) est sommable et de somme nulle. L'exemple a une grande importance, car il va intervenir dans le calcul de la moyenne des sommes partielles de Fourier! Plus étendu, l'article en allemand commence, lui, par rappeler que Dirichlet, et peut-être même Riemann, avaient cru à la convergence sans condition supplémentaire pour les fonctions continues, puis queDu Bois-Reymond avait mis un terme à cet espoir.
 |
 |
 |
| la note de Fejér aux CRAS (1900) |
Fejér jeune, à l'époque de sa trouvaille |
la version allemande, plus étendue (1903) |
On trouvera la genèse des idées de Fejér (et bien plus!) dans l'article de Jean-Pierre Kahane, Léopold Fejér et l'Analyse Mathématique au début du XXe siècle (1981)
- 1885, Weierstrass: un petit retour en arrière s'impose. Weirstrass avait prouvé un autre résultat rassurant; toute fonction continue peut être approchée uniformément sur un segment par des polynômes trigonométriques. (Donc, pas toujours des sommes de Fourier!). L'article, paru d'abord en allemand (épisode 1, épisode 2) est traduit dès l'année suivante au Journal de Liouville (épisode 1, épisode 2).
[N.B.:
Les articles de Weierstrass proviennent du site HAT: History of
Approximation Theory d'Allan Pinkus, d'une grande richesse en papiers
originaux.]
De façon immédiate, le théorème de Fejér fournit une nouvelle démonstration du résultat, beaucoup plus simple que celle de Weierstrass, et avec des approximants qu'on pourrait expliciter (en théorie au moins).
Deux Visions Révolutionnaires de l'Intégrale
Encore un retour en arrière, pour voir comment, au delà de la
seule question de laconvergence, les séries de Fourier ont
extraordinairement enrichi les mathématiques.Cela faisait deux bons siècles que sont nés les pères du Calcul Intégral, Newton et Leibniz, et que l'on somme à tour de bras. C'est pourtant en étudiant les séries trigonométriques et en s'interrogeant sur les coefficients de Fourier que deux mathématiciens vont poser les défintions modernes du concept de fonction intégrable. C'est la première des retombées inattendues de la théorie de Fourier... ce ne sera pas la seule!
Dirichlet a montré la nécessité de mieux préciser la notion à la fin de son article, avec un contre-exemple encore plus célèbre que celui qu'il a jeté à la figure de Cauchy
|
"...
l'intégrale d'une fonction ne siginfie quelque chose qu'autant que la
fonction satisfait à la condition précédemment énoncée. On aurait un exemple d'une fonction qui ne remplit pas cette condition , si l'on supposait φ(x) égale à une constante déterminée c lorsque la variable x obtient une valeur rationnelle, et égale à une autre constante d lorsque cette variable est irrationnelle. La fonction ainsi définie a des valeurs finies et déterminées pour toute valeur de la variable x, et cependant on ne saurait la substituer dans la série, attendu que les différentes intégrales qui entrent dans cette série, perdraient toute signification dans ce cas."
G. LEJEUNE-DIRICHLET, op.cit.
|
 |
 |
- 1854: Riemann. Le but de son travail est bien d'étendre les conditions de convergence de Dirichlet; et il donne ses raisons:
|
"Toutefois, ces cas non élucidés par Dirichlet semblent, pour une double raison, mériter l'attention. [...]
En second lieu, l'application des séries de Fourier n'est pas restreinte aux seules recherches physiques; on l'emploie maintenant avec succès dans une branche des mathématiques pures, la théorie des nombres, et ici ce sont précisément les fonctions dont Dirichlet n'a pas étusié la représentation en série trigonométrique qui semblent être les plus importantes." B. RIEMANN, op.cit.
|
Son
mémoire a commencé par un historique soigné, qui s'étend des cordes
vibrantes à la vaine attente d'une suite au mémoire de Dirichlet. La
formule intégrale des coefficients, présentée comme un coup de génie,
lui donne l'occasion d'un vibrant hommage à Fourier:
et d'un rappel de l'incompréhenssion à laquelle il se heurta:
|
 |
||
Mais ce sont ces mêmes coefficients qui l'amènent à poser la question fondamentale:

et à la résoudre en introduisant ce qui est resté sous la dénomination sommes de Riemann: la fonction est dite intégrable si elles ont toutes la même limite fixe lorsque les δj tendent vers 0.
La fonction de Dirichlet n'est pas intégrable au sens de Riemann.
- 1902-1906: Lebesgue.
|
"On
peut se demander, il est vrai, s'il y a quelque intérêt à s'occuper de
telles complications et s'il ne vaut pas mieux se borner à l'étude des
fonctions qui ne nécessitent que des définitions simples.
[...]Mais, si l'on voulait toujours se limiter à la considération
de ces bonnes fonctions, il faudrait renoncer à résoudre bien des
problèmes à énoncés simples posés depuis longtemps. C'est
pour la résolution de ces problèmes, et non par amour des
complications, que j'ai introduit dans ce Livre une définition de
l'intégrale plus générale que celle de Riemann et comprenant celle-ci comme cas particulier. [...]
Comme application de la définition de l'intégrale, j'ai étudié la recherche des fonctions primitives et la rectification des courbes. A ces deux applications j'aurais voulu en joindre une autre très importante : l'étude du développement trigonométrique des fonctions; mais, dans mon Cours, je n'ai pu donner à ce sujet que des indications tellement incomplètes que j'ai jugé inutile de les reproduire ici." H. LEBESGUE, Leçons sur l'Intégration et la Recheche des Fonctions Primitives.
|
Les secondes commencent par une introduction brève mais essentielle, sur la façon dont il faut envisager toutes les intégrales rencontrées dans l'étude des séries trigonométriques: elles devront être considérées au sens de sa nouvelle intégrale. Un des acteurs essentiels de son utilisation, Frédéric Riesz, témoignera avoir eu pour "déclencheur" cet ouvrage! (Son article et cette mention, ci-dessous).
Étudier ce remarquable ouvrage (qui est d'une grande clarté et n'est en rien démodé!) serait une digression trop longue dans notre sujet. Mais il est instructif de voir à l'œuvre la pédagogie de Lebesgue, le "révolutionnaire tranquille" qui se fait passer pour un... continuateur, avec une simple inversion du point de vue: le regroupement des valeurs de la fonction par leurs ordonnées plutôt que par les abcisses:
|
"Remarquons que notre définition constructive de l'intégrale est aussi très analogue à celle de Riemann; seulement,
alors que Riemann divisait en petits intervalles partiels l'intervalle
de variation de x, c'est l'intervalle de variation de f(x) que nous
avons subdivisé.
Cette façon d'opérer s'imposait, et ses avantages sont évidents. Lorsque l'on forme la somme S= f (ξi)[ xi+1- xi ] pour une fonction continue f(x), on groupe des valeurs de x fournissant des valeurs peu différentes de f(x) et c'est parce que ces valeurs sont peu différentes qu'on peut les remplacer dans S par l'une d'elles f(ξi). Mais, si f(x) est discontinue, il n'y a plus aucune raison que des choix d'intervalles (xi, xi+1) de plus en plus petits conduisent à grouper des valeurs de f (x) de moins en moins différentes. Et c'est pourquoi le procédé de Riemann ne réussit que rarement et en quelque sorte par hasard. Puisque nous voulons grouper des valeurs peu différentes de f(x), il est bien clair que nous devons, comme nous l'avons fait dans ce Chapitre, subdiviser l'intervalle de variation de f(x) et non l'intervalle de variation de x." H. LEBESGUE, Leçons sur l'Intégration et la Recheche des Fonctions Primitives.
|
ou, de manière encore plus imagée:
|
"Je
dois payer une certaine somme, disait-il; je fouille dans mes poches et
j’en sors des pièces et des billets de différentes valeurs. Je les
verse à mon créancier dans l’ordre où elles se présentent jusqu’à
atteindre le total de ma dette. C’est l’intégrale de Riemann. Mais
je peux opérer autrement. Ayant sorti tout mon argent, je réunis les
billets de même valeur, les pièces semblables et j’effectue le paiement
en donnant ensemble les signes monétaires de même valeur. C’est mon
intégrale."
H. LEBESGUE, cité par
A. DENJOY, L. FELIX, P. MONTEL Henri Lebesgue: le Savant, le Professeur, l'Homme
. |
Et c'est ainsi que la fonction de Dirichlet est intégrable au sens de Lebesgue!
Les deux noms sont aujourd'hui inséparables dans le remarquable énoncé de 3 mots, pas un de plus, que l'on donne aux étudiants de L3: "Lp est complet". Cet énoncé synthétise beaucoup de choses; il va très vite au but. N'importe qui est à même de comprendre que la voiture, le TGV et l'avion ont une utilité indéniable, mais vous privent trop souvent des charmes instructifs de la randonnée pédestre. Il en est de même ici: par sa progressivité naturelle, la promenade historique fera mieux apercevoir le paysage des vastes espaces... de Hilbert!
Pour commencer, la notation Lp n'existait pas encore: on parlait d'espace des fonctions de puissance p-ième sommable (c(est à dire intégrable en module ou valeur absolue), et pour le plus important d'entre eux, L2 , d'espace des fonctions de carré intégrable. Le "L" n'est venu qu'après, en hommage à Lebesgue, et ce geste dit déjà à lui seul que son intégrale est au cœur de ces résultats.
Ensuite, Riesz et Fischer ne s'intéressent dans leurs premiers articles respectifs, qu'au cas de L2 .
Alors, suivons un excellent guide, en savourant le commentaire qui suit la position du problème, qui concerne les séries de Fourier::
|
"Quelles relations y-a-t-il entre une fonction f et la suite (cn) de ses coefficients de Fourier?
Quelles propriétés de f peut on lire sur la suite (cn) , et réciproquement? La plus belle réponse à cette question est le théorème de Riesz-Fischer, obtenu indépendamment en 1907 par Frédéric Riesz et Ernest Fischer. [...] C'est pour [Riesz] le triomphe de l'intégrale de Lebesgue. Aujourd'hui, dans les cours sur l'intégrale de Lebesgue, on énonce souvent comme théorème de Riesz la proposition suivante: Lp est complet. Riesz n'a jamais énoncé un tel théorème. Pour la démonstration du théorème de Riesz-Fischer, il utilise un lemme, qui signifie en effet que L2 est complet. Mais les choses ne s'exprimaient pas de façon si compacte à l'époque. On n'avait pas encore baptisé l'espace L2, et la notion de complétion était encore implicite. Ainsi le lemme est devenu théorème , et l'essentiel du lemme est passé dans les définitions. [...] Ce qu'on prend aujourd'hui pour base d'une théorie, les définitions de base, sont bien souvent, historiquement, l'aboutissement de la théorie quand elle était en marche. Il est bien difficile, quand on enseigne ou simplement qu'on expose des mathématiques, de ne pas être infidèle à la démarche de la découverte." J.-P. KAHANE, journées X-UPS, École Polytechnique ( Mai 1989)
.
|
Le cas élémentaire des fonctions continues est une porte d'entrée commode: sonnez chez Pythagore et entrez! ... grâce à notre page dédiée! Vous y verrez comment établir élémentairement le résultat qu'on appelle inégalité de Bessel (et vou spourrez vous approcher de l'égalité):
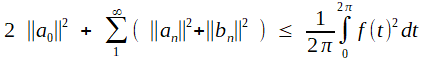
- Donnant des suites arbitraires de nombres (an) et (bn), telles que la série des carrés converge, existe-t-il une fonction dont ce sont les coefficients de Fourier?
- Si oui, est-elle de carré intégrable?
si pour ce problème sur les séries trigonométriques, l'intégrale de Lebesgue n'avait pas existé... il aurait fallu l'inventer!
Et c'est pourquoi Kahane est fondé à y voir le triomphe de l'intégrale de Lebesgue.
Riesz et Fischer inséparables... dans le temps aussi: ils firent leur découverte indépendamment, mais quasiment au même moment, et ils la publièrent à moins de deux mois d'intervalle. Il est teùps de revenir aux sources instructif de revenir aux sources et de comparer leurs contributions. Riesz prolonge les travaux de Hilbert sur les équations intégrales, et la référence aux coefficients de Fourier, éventuellement généralisés au cas d'un autre système orthogonal, est explicite. Fischer se positionne par rapport à Riesz: sans contester à celui-ci la primeur de publication, il prouve son indépendance par la date d'un exposé devant témoins. Mais, bien plus important, il va en donner une deuxième preuve, par sa démonstration qui est différente.différente

|

|
 |
 |
| La version de RIESZ ( lire l'article complet de Riesz) |
La version de FISCHER ( lire l'article complet de Fischer) |
|
Riesz répond à la question, qu'il a d'ailleurs lui-même posée au début
de son article, de la correspondance entre fonctions et séries des
coefficients de Fourier.
Sa réponse positive équivaut à la complétude, mais ce ne sera jamais dit en ces termes, seule l'expression de système complet -on dirait plutôt, de nos jours,système total- sera employée dans son papier. Bien des années après (voir ci-contre), il revient sur sa vision, en légitime et fier pionnier de l'utilisation de l'intégrale de Lebesgue, saluant l'influence décisive de ses Leçons sur les Séries Trigonométriques. Et trouve l'image juste!
|
 (lire l'article historique de Riesz) |
||
La formulation de Fischer, en revanche, est bien plus proche de notre présentation actuelle: c'est, très explicitement, le critère de Cauchy dans , qui affirme sa complétude pour la norme quadratique (noter que Fischer parle simplement de convergence en moyenne, mà où nous disons: convergence en moyenne quadratique. La théorie des espaces vectoriels normés va naître bientôt, avec Hilbert, Schmidt, Banach (voir notre page sur Banach & les espaces complets); les notations si commodes de produit scalaire et de norme sont encore absentes; on ne les verra guère arriver, par exemple, que dans le célèbre ouvrage de Riesz et Nagy, Leçons d'Analyse Fonctionnelle (1952).
La Naissance de la Théorie des Ensembles
|
"C'est à l'occasion de la théorie des séries trigonométriques que M. G. Cantor a commencé l'étude des ensembles de points."
H. LEBESGUE, Leçons sur les Séries Trigonométriques.
|
 |
Georg Cantor (1845-1918) met ses pas dans ceux de Riemann. Sur la suggestion de Heine,
il aborde le problème de l'unicité de l'écriture d'une série
trigonométrique partout convergente. Par différence, on le ramène à
celui-ci: si 0 = a0 + a1 cos x + b1 sin x + ... + an cos nx + bn sin nx + ...
cela entraîne-t-il que tous les coefficients sont nuls? Il y parvient en 1869, et cherche à généraliser, dans les cas où
la série converge sauf en un point, en un nombre fini de points, en une
infinité dénombrable de points... Tout ceci l'amène en 1872, dans
l'article Über die Ausdehnung eines Satzes aus der Theorie
der trigonometrischen Reihen,
(Mathematische Annalen, vol. 5, pp. 123-132, 1872) -c'est à dire: Sur la Généralisation d'un Théorème relatif aux Séries Trigonométriques, à définir les points d'accumulation, leur ensemble (ç y est, le mot est lâché!), dit ensemble dérivé, puis le dérivé du dérivé... puis à ce que l'on appellera plus tard la construction de Méray-Cantor des nombres réels, ceux-ci étant définis comme limites des suites de Cauchy de rationnels! (On
notera la formulation impeccable, moderne, du fameux critère, qui était
bien plus rustique et branlant chez celui dont il porte le nom).
 De là s'enchaîneront en 1874 la preuve qu'il y a plus de réels que de rationnels, dans un article sur la dénombrabilité des nombres algébriques (le célèbre procédé diagonal ne viendra qu'en 1891), et de 1879 et 1884 les six articles fondateurs de la théorie des ensembles. et de la théorie de la cardinalité. |
| Voilà donc Cantor, parti de Fourier, qui s'en éloigne de plus en plus... voire! Beatrice Lumpkin (AAAS & Malcom X College, Chicago) a suggéré que son célèbre ensemble tri-addique, construit par retraits successifs du tiers central d'un intervalle, lui aurait été suggéré par... un chapiteau égyptien de l'île de Philaé, vu dans la Description de l'Égypte, qu'il avait de bonnes raisons d'avoir feuiilleté: il avait un cousin égyptologue! On pourra accorder un sourire à cette anecdote, qui n'est pas... documentée de façon irréfutable. Mais, comme l'on dit en Italie: |
 |
Incidemment, ce n'est qu'après sa mort qu'il sera prouvé (Rajchman, 1921) que le tri-addique K de Cantor est un ensemble d'unicité: si la série trigonométrique converge vers 0 sauf sur K, elle est nulle. Mais... qu'au lieu d'enlever le tiers central à [0,1], on enlève ]ξ,1-ξ[, et qu'on réitère le procédé, on définit un ensemble K(ξ) qui généralise K=K(1/3), le résultat dépend de la valeur de ξ. Et, beaucoup plus déconcertant, d'une manière curieuse et subtile, révélant un lien secret avec un domaine des mathématiques a priori sans rapport, la théorie des nombres:
K(ξ) estensemble d'unicité: si et seulement si θ = 1/ξ est un nombre algébrique, vérifiant une condition technique annexe!
Vers une Généralisation des Fonctions
Immédiatement après la fin de la Seconde Guerre Mondiale, Laurent Schwartz publie... aux Annales de l'Institut Fourier (Grenoble), un article fondateur de sa théorie des distributions, pour laquelle il recevra la médaille Fields en 1950. La transformation de Fourier figure en bonne place dans le titre, et pour cause: la fonction constante égale à 1 (élément neutre multiplicatif pour les fonctions) a comme antécédent par la transformation de Fourier un objet bien moins orthodoxe, la "fonction de Dirac"... qui n'est pas une fonction! (lire notre encadré dans notre page sur la Transformée de Fourier)L'idée de Schwartz est d'interpréter les fonctions comme des densités de charge ou de masse (un rôle qu'elles assument couramment en physique); devenue "masse de Dirac", l'objet insolite s'assimile à une charge ponctuelle et l'idée de distribution (au sens : "distribution de charge" englobe alors les deux. Bien sûr, faire fonctionner cette idée demande encore du travail; lidée géniale est de faire opérer ces objets sur les fonctions indéfiniment dérivables, à "support compact" ou à "décroissance rapide à l'infini".
 l'article fondateur (Annales de l'Institut Fourier) |
|
| Pendant la guerre, Laurent Schwartz et son épouse sont, pour leur sécurité, contraints à employer une fausse identité! (Archives de l'École Polytechnique)
|
|
 (l'article complet à télécharger) |
Tout en "dénonçant" l'emploi hardi de procédés inavouables par les physiciens et ingénieurs, Schwartz reconnaît leur "succès incontestable" , leurs"constants services en éléctricité",et leur "grande adaptation à l'étude de la transformation de Fourier" ; aussi n'hésite-t-il pas à s'adresser à ces catégories dans leurs revues pour populariser sa théorie et montrer qu'elle apporte le fondement mathématique qui manquait jusqu'alors à cet emploi empirique. |
| On est loin, très loin du refus des applications jugées dégradantes pour les mathématiques pures d'un certain Bourbaki, à la même époque, et du mépris absolu dans lequel il tient Fourier et son œuvre: une seule page en parle, et sous quel titre improbable! Avec quelle consdescendance sur l'originalité de son travail! On en viendrait à comprendre pourquoi les rédacteurs ont préféré se réfugier derrière un pseudonyme... |
|
Références
- J.-P. KAHANE, P.-G. LEMARIÉ, Séries de Fourier et Ondelettes (Cassini)
- F. RIESZ, B. NAGY, Leçons d'Analyse Fonctionnelle (3ème éd, J. Gabay) ou Fonctiunal Analysis (Dover)
- W. RUDIN, Analyse Réelle et Complexe (Dunod)
- C. ZUILY, H. QUEFFELEC, Éléments d'Analyse pour l'Agrégation (Masson)
Poursuivre...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Revenir à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Revenir à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique