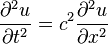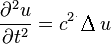Harmonique, vous avez dit: Analyse Harmonique?
... Une Promenade Fouriériste! (Partie 0.2)
Nous poursuivons ici notre vagabondage musical en compagnie de l'équation des ondes. Les mathématiques y seront un peu plus présentes et un peu plus compliquées que dans le cas des cordes, mais pas tant que cela: la merveilleuse simplicité de la méthode de séparation des variables de Fourier ramène vite au cas unidimensionnel, et nous avons surtout en vue la recherche des modes propres associée, sans s'occuper ici de leur sommation. Alors, pour commencer... roulez, tambours!
Pourquoi les Tambours sont-ils Circulaires?
Avant de vous poser ce genre de questions, écoutez donc ces deux monstres de l'instrument sur le célébrissime Night in Tunisia: Art Blakey, Elvin Jones. |
 |
| Art Blakey (et ses Jazz
Messengers) Nice, jardins de Cimiez, 18 Juillet 1988, 20h |
Elvin Jones (et sa Jazz Machine)
Nice, jardins de Cimiez, 14
Juillet 1993, 20h
|
L'équation des membranes
vibrantes a la même forme que celle des cordes: dans ce dernier
cas, la dérivée seconde en x est un laplacien réduit à une seule variable. On a donc deux coordonnées d'espace (x, y) repérant un point M de la membrane; la célérité de propagation de l'onde est ici notée c.
Les conditions initiales correspondent à une corde ou
membrane au repos, frappée... bien frappée sur nos images!
 Charlie Haden à Nice, Jardins de Cimiez, 17/07/88, 19h |
cordes | QUI vibre? | membranes |
 Poncho Sanchez
Nice, Arènes de Cimiez, 10/07/89, 19h |
| y = u (x, t) | inconnue | z = u (x, y ; t) | ||
 |
évolution | 
|
||
| u (0, t) = 0 u (L, t) = 0 |
conditions au bord |
u (a, b ; t) = 0 pour P(a, b) au bord |
||
u (x, 0) = 0 |
conditions initales | u (x, y, 0) = 0 |
La méthode de Fourier séparera, dans un premier temps, les variables de temps et d'espace, en
cherchant les fonctions
u(x, y, t) = v(x, y) . w(t)
On obtient ainsi deux équations, dont la première est toujours une équation aux dérivées partielles, dite équation d'Helmholtz, et qu'on peut interpréter "savamment" comme recherche des valeurs propres du laplacien. | variables | |
| d'espace | Δ v(x, y) = λ v(x, y) |
| de temps | w"(t) = λc² w(t) |
| conditions au bord |
v (a, b) = 0 si le point P(a, b) est au bord |
Et d'abord, pourquoi pas carrés?
Si le tambour est un carré, x et y sont astreints à varier entre 0 et L, d'où les conditions aux limites: v(x, 0) = 0, v(x, L) = 0, v(0, y) = 0, v(L, y) = 0
On sépare maintenant les deux
variables d'espace, ce qui paraît approprié à la
géométrie du tambour:
v(x, y) = h(x) . k(y)
h et k vont vérifier chacune une équation différentielle du second ordre de la forme h" + αh =0 , mais (petit exercice...) seules les constantes α > 0 pourront permettre de satisfaire les deux conditions en 0 et L; on écrit donc directement ces constantes comme des carrés.
| variable | x | y | t |
| équation | h"(x) + μ² h(x) = 0 | k"(y) + ν² k(y) = 0 | w"(t) + (μ² + ν²) c² w(t) = 0 |
| conditions au bord |
h (0) = 0 h (L) = 0 |
k (0) = 0 k (L) = 0 |
|
| conditions initales | u (x, 0) = 0 |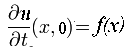
u (x, y, 0) = 0 |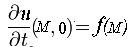
On retrouve en fait les équations du cas de la corde: c'est un peu comme si chaque parallèle à un côté du carré vibrait comme une corde!
h est donc une sinusoïde h(x) = A sin μx + B cos μx, et les conditions aux limites imposeront B = 0, puis μ= nπ /L, n entier naturel. Pour le dire de façon plus imagée, ce sont les seules valeurs qui règlent correctement l'écartement de la sinusoïde pour qu'elle passe par 0 en x = 0, x = L; ou enfin, c'est le calcul mathématique qui justifie la découverte expérimentale des harmoniques par Sauveur.
On obtient donc les solutions "séparées":
un,p (x, y, t) = sin ( nπx /L) . sin ( pπy /L) . sin (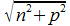
πct/L )
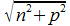πct/L )Oui, mais voilà: n² + p² n'est que très rarement un carré d'entier q² (ex: n = 3, p = 4, q = 5) et la plupart du temps q est irrationnel. Dès lors, les fréquences temporelles du dernier sinus ne sont pas les multiples entiers d'une même fréquence, et le son est très mélangé... ce qui risque bien lui valoir le qualificatif de bruit!
N.B.: en cherchant bien... il existe un instrument de cette forme, ou plus exactement parallélépipédique (une dimension supplémentaire n'arrange rien, on devine aisément comment modifier la forme de la solution ci-dessus): c'est le cajón péruvien, à l'origine sans doute, un simple cageot destiné à la cueillette des fruits, et sa variante cubaine le cajón tumbadora, ou cajón de rumba. Qui, entre les mains d'un bon percussioniste -mais à Cuba, c'est un pléonasme!- s'avère nettement plus agréable que le matériel hypersophistiqué de batteurs aussi mauvais que prétentieux, remplissant pourtant les conditions mathématiques que nous allons évoquer maintenant...
N.B.: en cherchant bien... il existe un instrument de cette forme, ou plus exactement parallélépipédique (une dimension supplémentaire n'arrange rien, on devine aisément comment modifier la forme de la solution ci-dessus): c'est le cajón péruvien, à l'origine sans doute, un simple cageot destiné à la cueillette des fruits, et sa variante cubaine le cajón tumbadora, ou cajón de rumba. Qui, entre les mains d'un bon percussioniste -mais à Cuba, c'est un pléonasme!- s'avère nettement plus agréable que le matériel hypersophistiqué de batteurs aussi mauvais que prétentieux, remplissant pourtant les conditions mathématiques que nous allons évoquer maintenant...
Le cercle, PRESQUE l'Harmonie...
Il semblerait que les latinos apprécient quand même davantage le cercle que le carré: |
 |
| Tito Puente (timbales), Giovanni Hidalgo (bongo), Ignacio Berroa (congas), Nice, jardins de Cimiez, 17 Juillet 1993, 20h |
Mongo Santamaria (congas)
Nice, jardins de Cimiez, 18
Juillet 1991, 22h
|
Savourez le célébrissime Oye Como Va de Tito (eh oui... Carlos Santana n'a fait que le reprendre!), les danseuses sont offertes sans supplément; et Mongo Santamaria dans sa carte de visite Afro Blue (eh oui... John Coltrane n'a fait que le reprendre!)... et passons aux équations!
Le travail est complètement similaire à celui qu'a fait Fourier dans le cas du cylindre. Nous vous suggérons d'ailleurs d'ouvrir une deuxième fenêtre sur ce sujet, et de la juxtaposer à celle-ci, pour mieux voir que presque rien ne change. On aura encore recours aux coordonnées polaires, et, dans un premier temps au moins, on recherchera les solutions radiales.
Le laplacien a pour expression (rappel: r² =x² + y² )
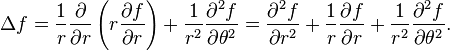
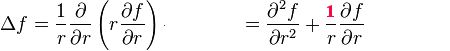
L'équation d'Helmholtz se
réduit à une équation différentielle
à une variable lorsqu'on sépare les variables :
Le seul changement est donc l'équation en t, qui est du second ordre au lieu du premier, conséquence logique de la substitution d'une dérivée partielle seconde temporelle à la dérivée première du cas de la chaleur (voir l'encadré comparatif dans la page relative à la chaleur).
Arrivent maintenant les deux faits importants:
1. J0 possède une une infinité dénombrable de racines, que l'on nommera ζk . Cela va permettre de vérifier la condition au bord avec des solutions non triviales, Tout se passe comme avec sin, mais ces racines ζk prennent la place des kπ. Ainsi peut-on proposer des solutions fondamentales à variables séparées:
ou la forme similaire en cosinus; la première rend évidente le repos de la membrane au temps t=0 pour toute combinaison de ces solutions.
2. Les ζk forment presque une progression arithmétique (ce qui siginifie que l'écart entre deux racines est presque constant). Qualitativement, cela peut se voir avec la formule approximative
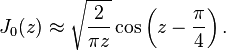Elle est théoriquement valable "pour z
assez grand", mais, en pratique, assez tôt comme on peut le voir
en superposant les deux graphes.
La table qui suit explicite la comparaison des racines:
De la proximité des graphes résulte celle des ζk avec les (k-1)π + 3π/4 qui sont les racines de la formule approximative et correspondraient à une harmonie parfaite.
On se ramène cette fois à l'équation générale de Bessel (les solutions radiales étaient données par le cas n=0)
dont on utilise la seule solution bornée en 0, à un facteur près, la fonction Jn de Bessel dont les zéros sont notés ζn,k :
Il y a donc une famille de modes propres plus importante, mise en évidence expérimentalement par Ernst Chladni (1756-1827) en plaçant du sable sur des peaux de tambour, frottées avec un archet (voir l'expérience ici, par exemple).
Voir aussi cet article de Serge Cantat sur le site Image des Mathématiques (CNRS)
u(x, y, t) = v (r, t) = j(r). w(t)
On
aura respectivement, R étant le rayon du tambour:| en t | w"(t) = λc² w(t) |
| en r | r j"(r) + u'(r) - λr j(r) = 0 |
| au bord | j(R) = 0 |
Le seul changement est donc l'équation en t, qui est du second ordre au lieu du premier, conséquence logique de la substitution d'une dérivée partielle seconde temporelle à la dérivée première du cas de la chaleur (voir l'encadré comparatif dans la page relative à la chaleur).
| Petit passage technique... (que vous pouvez sauter en admettant les réultats!)
On cherche les solutions
développables en série entière, et l'on montre que
la condition au bord ne peut être vérifiée avec des
λ>0. Ainsi l'équation en t aura-telle des solutions oscillantes, ce à quoi l'on s'attendait. On peut donc écrire λ = -γ²,
faire ce petit changement de variable dans
l'équation différentielle pour retrouver la plus simple des équations de Bessel (ou biographie en allemand
bien plus complète!)
Toutes ses solutions sont de la forme A.J0 + B.Y0 , mais la fonction Y0 présente un grave inconvénient pour un tambour: elle n'est pas bornée à l'origine! Si l'on veut éviter de voir le tambour crevé en son centre, autant l'éviter, de sorte qu'il reste j(r) = A J0
( γ
r)
|
Arrivent maintenant les deux faits importants:
1. J0 possède une une infinité dénombrable de racines, que l'on nommera ζk . Cela va permettre de vérifier la condition au bord avec des solutions non triviales, Tout se passe comme avec sin, mais ces racines ζk prennent la place des kπ. Ainsi peut-on proposer des solutions fondamentales à variables séparées:
vk (r, t) = J0
( ζk
r/R) . sin ( ζk ct/R)
ou la forme similaire en cosinus; la première rend évidente le repos de la membrane au temps t=0 pour toute combinaison de ces solutions.
2. Les ζk forment presque une progression arithmétique (ce qui siginifie que l'écart entre deux racines est presque constant). Qualitativement, cela peut se voir avec la formule approximative
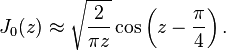
La table qui suit explicite la comparaison des racines:
| k | 1 | 2 | 3 | 4 | 5 | 10 | 15 |
| ζk | 2,405 | 5,520 | 8,654 | 11,792 | 14,931 | 30,634 | 46,341 |
| (k-1)π + 3π / 4 | 2,356 | 5,498 | 8,639 | 11,781 | 14,922 | 30,631 | 46,338 |
De la proximité des graphes résulte celle des ζk avec les (k-1)π + 3π/4 qui sont les racines de la formule approximative et correspondraient à une harmonie parfaite.
Et voilà pourquoi on
entend chanter les tambours d'un Art Blakey (réécoutez
Night in Tunisia!) ou d'un Max Roach!
Remarque: et plus généralement...
On peut trouver abusive la recherche d'une solution radiale de l'équation d'Helmholtz -on peut d'ailleurs en douter aisément si le tambour n'est pas frappé initialement en son centre, mais en un point quelconque. Toutefois seules de légères corrections serontà apporter si l'on poursuit la séparation des variables pour les paramètres de distance radiale et d'écart angulaireu(x, y, t) = v (r, θ, t) = j(r). k(θ). w(t)
| en θ | k"(θ) = - n² k(θ) |
| en r | j"(r) +(1/r) u'(r) +(γ²/c²- n²/r²) j(r) = 0 |
| au bord | j(R) = 0 |
On se ramène cette fois à l'équation générale de Bessel (les solutions radiales étaient données par le cas n=0)
Y"(r) +(1/r) Y'(r) +(1- n²/r²) Y(r)
= 0
dont on utilise la seule solution bornée en 0, à un facteur près, la fonction Jn de Bessel dont les zéros sont notés ζn,k :
vn,k (r, θ, t ) = Jn
( ζn,k
r/R). sin (nθ + ψ) . sin ( ζn,k ct/R)
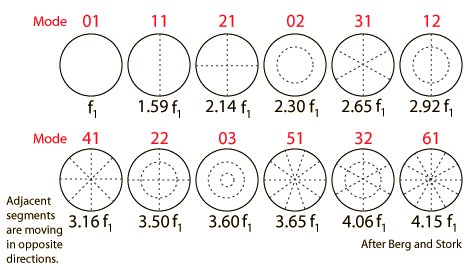
Il y a donc une famille de modes propres plus importante, mise en évidence expérimentalement par Ernst Chladni (1756-1827) en plaçant du sable sur des peaux de tambour, frottées avec un archet (voir l'expérience ici, par exemple).
 |
 |
|
Figures de Chladni,
avec les rapports des fréquences à la fondamentale ζn,k / ζ0,1
|
Figures de Chladni, sable sur plaques métalliques (exposition Fourier, IHP Paris, juin 2018)
|
Voir aussi cet article de Serge Cantat sur le site Image des Mathématiques (CNRS)
Peut-on entendre la forme d'un tambour?
|
Cette question peut surprendre avec sa feinte naïveté enfantine... mais
les enfants posent parfois des questions très intelligentes. Elle est
le titre d'un célèbre article de Mark Kac, écrit en 1966... et dont la réponse
ne fut pas donnée avant1992!
Nous avons jusqu'ici montré qu'un tambour carré et un tambour circulaire n'ont pas les mêmes modes propres, ou fréquences propres, de vibration. On peut aussi effectuer les calculs pour un tambour elliptique -la chose se complique encore, et fait appel à une nouvelle famille de fonctions, dites de Mathieu, en remplacement de celles de Bessel. Cela peut vous paraître une idée saugrenue pour un tambour, mais ce n'est rien en comparaison de ce qui vous attend quelques lignes plus bas... en tout cas, on trouverait une troisième famille de modes propres. Autrement dit, ces trois tambours sont identifiables en aveugle, au moins par un instrument de laboratoire qui affichera leur spectre (ensemble des modes propres). Le problème est de savoir si cela se généralise, ou si, au contraire, il est possible que deux tambours de formes distinctes aient rigoureusement le même ensemble de modes propres. Mathématiquement, ce spectre est celui du laplacien dans le domaine considéré, puisqu'il s'agit de déterminer les λ pour qui l'on a Δ v = λ v
c'est à dire, pour tout point M (x, y) du domaine -la peau du tambour: |
 |
| La première page de l'article de Kac, avec l'équation des ondes. |
|
 |
 |
|
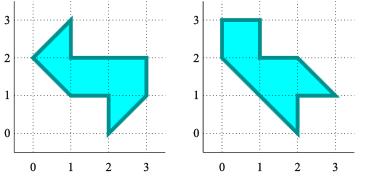
Le premier contrexemple:
Gordon, Webb & Wolpert (1992) |
Un contrexemple simple, sur la page Wikipedia dédiée |
Cet article fait un point récent (2010) sur la question (dont des conditions permettant d'assurer la caractérisation par le spectre: théorème de Zelditch, 2009).
Autres Instruments à Percussion
Percussions à lames: le vibraphone
Avant d'affronter les
équations, pour vous donner du courage, un petit coup
d'œil... et d'oreille aux deux maîtres historiques de
l'instrument:
 |
 |
|
Lionel
Hampton, dans son costume spécialement réalisé pour
célébrer le bicentenaire de la Révolution
Française... un an après!
Nice, jardins de Cimiez, 12 Juillet 1990, 22h |
Milt Jackson avec le Modern Jazz Quartet Nice,arènes de Cimiez, 11 Juillet 1982, 19h |
Lionel Hampton a fait date dans l'histoire avec ses deux enregistrements de Flying Home en 1942: le premier avec Illinois Jacquet au sax ténor, le second avec Arnett Cobb sur le même instrument. Pour profiter d'une vidéo, pourquoi pas cette version de 1957? Autre classique, Hamp's Boogie-Woogie, ici en 1988...
Milt Jackson est l'un des quatre piliers du Modern Jazz Quartet: admirez leur complicité dans True Blues, et retrouvez Milt avec un autre groupe dans son emblématique Bag's Groove.
Tout cela est fort bon, mais avec les lames, l'équation définissant la vibration se complique. Pourquoi? Sans entrer trop dans le détail de la physique, il est intéressant de voir que cela résulte du fait que le système est mainteant régi par deux équations et deux fonctions inconnues.On étudie, comme dans le cas d'une corde, l'élongation transversale y (x, t). Mais en plus intervient une deuxième fonction qui prend en compte le fait que la lame se courbe: le cas le plus évident est celui d'une règle métallique souple fermement tenue à une extrémité, que l'on fait osciller en agissant sur l'extrémité libre, mais il en va de même pour une lame frappée par la mailloche.
Oublions un instant le temps: cette déformation fait intervenir une fonction M(x), appelée moment de flexion, inversement proportionnelle au rayon de courbure R(x) de la lame à l'abcisse x. On a , avec des constantes E et I (E en particulier prend en compte la nature du matériau, c'est son module de Young)
Milt Jackson est l'un des quatre piliers du Modern Jazz Quartet: admirez leur complicité dans True Blues, et retrouvez Milt avec un autre groupe dans son emblématique Bag's Groove.
Tout cela est fort bon, mais avec les lames, l'équation définissant la vibration se complique. Pourquoi? Sans entrer trop dans le détail de la physique, il est intéressant de voir que cela résulte du fait que le système est mainteant régi par deux équations et deux fonctions inconnues.On étudie, comme dans le cas d'une corde, l'élongation transversale y (x, t). Mais en plus intervient une deuxième fonction qui prend en compte le fait que la lame se courbe: le cas le plus évident est celui d'une règle métallique souple fermement tenue à une extrémité, que l'on fait osciller en agissant sur l'extrémité libre, mais il en va de même pour une lame frappée par la mailloche.
Oublions un instant le temps: cette déformation fait intervenir une fonction M(x), appelée moment de flexion, inversement proportionnelle au rayon de courbure R(x) de la lame à l'abcisse x. On a , avec des constantes E et I (E en particulier prend en compte la nature du matériau, c'est son module de Young)
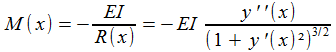
selon la formule mathématique
donnant le rayon de courbure: quelques connaissances de
géométrie peuvent toujours être utiles! Il reste
alors à se dire qu'en pratique, y'(x) n'est pas très grand, donc son carré est négligeable: cela permet de linéariser cette formule en
M(x) = - EI y"(x)
Enfin, revenant à une fonction y (x, t),
la dérivée seconde doit être remplacée par
la dérivée partielle correspondante, ce qui fournit la
première équation. La deuxième se contente de
traduire la relation fondamentale de la dynamique; en combinant les
deux, l'équation en y est du quatrième ordre!| moment de flexion |  |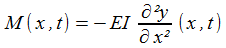
| relation fondamentale de la dynamique |
 |
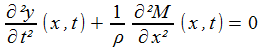| synthèse |  |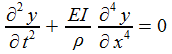
Tout ceci est connu comme théorie des poutres d'Euler-Bernoulli.
L'équation étant linéaire (mais pas d'hypocrisie:
c'est nous qui l'avons rendue telle par l'approximation ci-dessus!),
elle se prête à la méthode de séparation des
variables aussi bien que les précédentes.
Pour un vibraphone, les extrémités de la lame (de longueur L) sont libres: cela peut surprendre de prime abord, pourtant, revoyez le Bag's Groove de Milt Jackson, vous devriez être convaincu... La traduction mécanique en est l'annulation des dérivées partielles secondes et troisièmes aux abcisses limites, à tout instant t; on les a transcrites sur v.
La fin de l'histoire n'est qu'une variante des précédentes: résoudre une équation à coefficients constants du 4ème ordre n'est pas plus difficile qu'au second, à partir de l'équation caractéristique
y (x, t) = v (x). w(t)
Comme dans le cas des tambours, l'équation obtenue en t, w"(t) + μ w(t)
= 0 ne fournira des oscillations que dans le cas μ
= ω2 ; on s'y limite d'emblée. On
aura alors respectivement, en posant α4 = ρ ω2 / EI | en t | w"(t) + ω² w(t) = 0 |
| en x | v(4)(x) - α4 v(x) = 0 |
| aux extrémités, x = 0, x = L |
v"(0)
= 0 , v(3)(0)
= 0 v"(L) = 0 , v(3)(L) = 0 |
Pour un vibraphone, les extrémités de la lame (de longueur L) sont libres: cela peut surprendre de prime abord, pourtant, revoyez le Bag's Groove de Milt Jackson, vous devriez être convaincu... La traduction mécanique en est l'annulation des dérivées partielles secondes et troisièmes aux abcisses limites, à tout instant t; on les a transcrites sur v.
La fin de l'histoire n'est qu'une variante des précédentes: résoudre une équation à coefficients constants du 4ème ordre n'est pas plus difficile qu'au second, à partir de l'équation caractéristique
r4 - α4
= (r2 - α2 )(r2 + α2 ) = 0
on tire
y (x, t) = (A sin αx + B cos αx + C sh αx + D ch αx). sin (ωt + φ)
Les conditions en 0 donnent, à vue, A = C et B = D, et, en L, se traduisent par:
Les conditions en 0 donnent, à vue, A = C et B = D, et, en L, se traduisent par:
A (sh αL - sin αL) + B (ch αL - cos αL) = 0
A (ch αL - cos αL) + B (sh αL +sin αL) = 0
Ce système ne peut avoir de solution que si son déterminant est nul
La recherche des modes propres s'avère, au vu de la géométrie circulaire, plus commode en coordonnées polaires; la forme des solutions séparées emploie les fonctions de Bessel Jn mentionnées plus haut et leurs "cousines", dites modifiées, In :
Les conditions au bord, plus délicates, n'ont été formulées avec exactitude qu'en 1850, par Kirchhoff: sur ce point, Sophie Germain s'était trompée. L'important pour notre propos est de savoir qu'elles conduisent de nouveau à des familles de modes propres, calculables numériquement; autrement dit, la méthode de Fourier réussit pleinement dans ce cas qui mêle la complexité des deux précédents.
200 ans après ses premiers travaux sur la vibration des plaques (et 240 ans après sa naissance), la Poste Française a la bonne idée d'émettre un timbre en l'honneur de Sophie Germain; il évoque, outre les recherches que nous venons de présenter, sa célèbre avancée sur le Grand Théorème de Fermat. Son lancement aura mieu le 18 Mars 2016, dans le cadre d'une journée commémorative (voir le communiqué de presse) à l'Institut Henri Poincaré (Paris).
A (ch αL - cos αL) + B (sh αL +sin αL) = 0
Ce système ne peut avoir de solution que si son déterminant est nul
sh² αL - sin² αL - (ch αL - cos αL)² = 0
et, par la magie des relations ch² u - sh² u = 1 et cos² u + sin² u = 1
et, par la magie des relations ch² u - sh² u = 1 et cos² u + sin² u = 1
ch λ . cos λ = 1 ; λ = αL
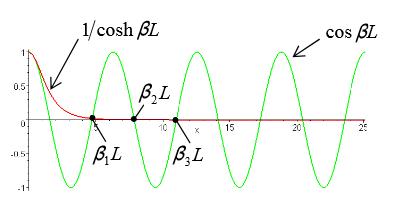
Bien sûr, cette équation ne peut être résolue que numériquement, mais, en revanche, on démontre que sa kième racine λk est proche de (2k + 1)π / 2 à l'ordre de grandeur e-n près.
Et d'ailleurs, cela saute aux yeux sur une figure où l'on trace les courbes cos et 1/ ch:
Les fréquences de vibration ω/2π sont proportionnelles aux α² , soit aux λ².
Donc, comme dans le cas des tambours, les rapports de fréquences propres sont "presque des rapports d'entiers", ce qui assure une perception proche de l'harmonie parfaite.
En pratique, les lames, au lieu d'être des parallélépipèdes minces, sont plus creusées au centre, sur la face inférieure, pour perfectionner la justesse: il s'agit là d'un travail empirique de facteurs d'instruments, non de modélisation théorique! Et, quoiqu'il y ait changement de matière (on passe du métal au bois), la théorie reste la même pour le marimba...
Joueur de marimba au Guatemala
Assez grossièrement, elles peuvent être modélisées par des plaques circulaires minces, planes (Dans la réalité, ce sont des cônes très évasés). Mathématiquement, tout se passe comme si l'on combinait les "difficultés" des cas du tambour et des lames: on y rencontre à la fois une équation du quatrième ordre et des fonctions de Bessel! Aussi passerons nous assez rapidement... mais comment taire dans ces pages consacrées à Fourier que c'est la jeune mathématicienne qu'il a encouragée et soutenue, Sophie Germain, qui a la première, en 1816, formé correctement l'équation qui les régit?
Le soutien de Fourier, alors à la position stratégique de secrétaire perpétuel de l'Académie, est attesté par plusieurs courriers, privés ou officiels; qu'on juge de sa vigilance contre tout coup de griffe de son "vieil ennemi" Poisson!
Sophie, quant à elle, rend un hommage direct au soutien de Fourier dès la préface de son ouvrage:
N.B.: Le mémoire complet de Sophie Germain est en ligne ici; et là une étude se son travail par Amy Dahan-Dalmédico (plus généralement, ce site regroupe pas mal d'informations sur sa vie et son œuvre. )
L'équation des cymbales fait intervenir un "double laplacien", c'est à dire le laplacien du laplacien
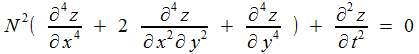
Bien sûr, cette équation ne peut être résolue que numériquement, mais, en revanche, on démontre que sa kième racine λk est proche de (2k + 1)π / 2 à l'ordre de grandeur e-n près.
| k | 1 | 2 | 3 | 4 | 5 |
| λk | 4,730 | 7,853 2 | 10,995 61 | 14,137165 | 17,278 759 65 |
| (2k + 1)π / 2 | 2,356 | 7,853 9 | 10,995 57 | 14,137167 | 17,278 759 59 |
Et d'ailleurs, cela saute aux yeux sur une figure où l'on trace les courbes cos et 1/ ch:
Les fréquences de vibration ω/2π sont proportionnelles aux α² , soit aux λ².
Donc, comme dans le cas des tambours, les rapports de fréquences propres sont "presque des rapports d'entiers", ce qui assure une perception proche de l'harmonie parfaite.
En pratique, les lames, au lieu d'être des parallélépipèdes minces, sont plus creusées au centre, sur la face inférieure, pour perfectionner la justesse: il s'agit là d'un travail empirique de facteurs d'instruments, non de modélisation théorique! Et, quoiqu'il y ait changement de matière (on passe du métal au bois), la théorie reste la même pour le marimba...
Joueur de marimba au Guatemala
Les Cymbales
 |
 |
|
Elvin Jones (et sa Jazz Machine)
Nice, jardins de Cimiez, 15 Juillet 1993, 19h |
Roy Haynes (sous l'œil du ténor Craig Handy)
à l'avant de la scène, avec sa seule cymbale high hat! Nice, jardins de Cimiez, 12
Juillet 1990, 23h
|
Assez grossièrement, elles peuvent être modélisées par des plaques circulaires minces, planes (Dans la réalité, ce sont des cônes très évasés). Mathématiquement, tout se passe comme si l'on combinait les "difficultés" des cas du tambour et des lames: on y rencontre à la fois une équation du quatrième ordre et des fonctions de Bessel! Aussi passerons nous assez rapidement... mais comment taire dans ces pages consacrées à Fourier que c'est la jeune mathématicienne qu'il a encouragée et soutenue, Sophie Germain, qui a la première, en 1816, formé correctement l'équation qui les régit?
 |
 |
|
| Billet manuscrit de Fourier: il s'invite à passer la voir un soir! (source: Gallica BnF) |
Paris, 13 rue de Savoie:
dernière demeure de Sophie Germain. |
|
Le soutien de Fourier, alors à la position stratégique de secrétaire perpétuel de l'Académie, est attesté par plusieurs courriers, privés ou officiels; qu'on juge de sa vigilance contre tout coup de griffe de son "vieil ennemi" Poisson!
| "Mademoiselle, Je regrette extrêmement de n'avoir pu répondre aussi promptement que je l'aurais désiré au sujet du Mémoire de Mathématiques que vous nous avez envoyé. Je me suis acquitté fidèlement de la commission que vous m'aviez donnée en m'adressant cette pièce. [...] Si M. Poisson a le dessein de montrer quelque opposition au résultat de vos recherches, il ne pourra s'empêcher de céder à l'autorité de l'expérience que personne ne sait consulter mieux que vous. Autant que j'ai pu prendre connaissance de la discussion dont vous vous êtes occupée, il m'a paru que vous mettez dans tout son jour l'insuffisance de l'hypothèse théorique dont il a voulu déduire l'équation du quatrième ordre, que vous avez trouvée. [...] Toutes les personnes présentes à la séance ont entendu avec le plus grand intérêt l'annonce de votre Mémoire. La difficulté du sujet, la célébrité des auteurs qui l'ont traité et votre nom ne pouvaient manquer d'exciter l'attention. Nous nous en sommes entretenus avec plusieurs personnes à l'Académie et chez M. de Laplace. Je vous remercie, Mademoiselle, des nouvelles marques d'intérêt que vous me donnez en vous occupant de ma santé et de mes travaux. C'est une obligation fâcheuse que celle des discours publics, et les personnes dont j'estime le plus les suffrages sont celles que je crains le plus d'avoir pour auditeurs. [...] " Fourier, Lettre à Sophie Germain, 12 Mars 1824)
|
 Le courier officiel (probablement écrit par un secrétaire) envoyé 3 jours plus tard...
|
Sophie, quant à elle, rend un hommage direct au soutien de Fourier dès la préface de son ouvrage:
 |
 |
Le Mémoire de Sophie Germain fut publié à compte d'auteur, en 1821. Page où Sophie Germain obtient l'équation, dans un cadre général d'abord, puis celui qui nous intéresse ici. (Source des images: page de titre:Wikipedia page de calculs: Gallica BnF) |
|
"La
Classe accorda le prix à mon Mémoire; mais elle
annonça pourtant que ma démonstration ne lui avait pas
paru entièrement satisfaisante.
Depuis cette époque, je me suis occupée, à diverses reprises , de la théorie des surfaces élastiques. J'ai multiplié les expériences, les calculs et les réflexions. J'avouerai que j'ai toujours cru voir de nouveaux motifs pour tenir à mon opinion. Je me disposais à publier mes raisons, lorsque M. Fourier voulut bien prendre connaissance de ma démonstration. Ce juge éclairé témoigna qu'il préférait aux raisonnemens sur lesquels je m'appuyais, une démonstration purement géométrique; il me proposa pour modèle celle que Jacques Bernoulli avait autrefois donnée pour l'hypothèse relative au cas de la lame droite. Cette démonstration semblait être tombée dans l'oubli; j'en ignorais entièrement l'existence. Fondée sur la manière dont s'expriment Euler et surtout M. de Lagrange (Mécan. analytique, Mém. sur les Ressorts ployés) , j'avais toujours cru que l'hypothèse n'avait été admise que comme une supposition purement arbitraire. Le Mémoire de Bernoulli me parut obscur. M. Fourier poussa la complaisance jusqu'à prendre la peine de me l'expliquer. Je me plais à reconnaître que, sans le secours de cet habile géomètre, je n'aurais su ni apprécier ni même entendre la démonstration de l'auteur." Sophie Germain, Préface des Recherches sur la Théorie des Surfaces Élastiques, 1821
|
||
N.B.: Le mémoire complet de Sophie Germain est en ligne ici; et là une étude se son travail par Amy Dahan-Dalmédico (plus généralement, ce site regroupe pas mal d'informations sur sa vie et son œuvre. )
L'équation des cymbales fait intervenir un "double laplacien", c'est à dire le laplacien du laplacien
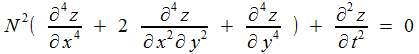
Y séparer les variables d'espace et de temps revient à écrire, une fois de plus
| variables | |
| d'espace | Δ [Δ v] (x, y) = ω²/N² . v(x, y) |
| de temps | w"(t)+ ω² w(t) = 0 |
La recherche des modes propres s'avère, au vu de la géométrie circulaire, plus commode en coordonnées polaires; la forme des solutions séparées emploie les fonctions de Bessel Jn mentionnées plus haut et leurs "cousines", dites modifiées, In :
z (x, y; t) = Z (r, θ; t) = [ A Jn
( α
r) + B In
( α
r) ] . sin (nθ + ψ) . sin (ωt + φ)
Les conditions au bord, plus délicates, n'ont été formulées avec exactitude qu'en 1850, par Kirchhoff: sur ce point, Sophie Germain s'était trompée. L'important pour notre propos est de savoir qu'elles conduisent de nouveau à des familles de modes propres, calculables numériquement; autrement dit, la méthode de Fourier réussit pleinement dans ce cas qui mêle la complexité des deux précédents.
200 ans après ses premiers travaux sur la vibration des plaques (et 240 ans après sa naissance), la Poste Française a la bonne idée d'émettre un timbre en l'honneur de Sophie Germain; il évoque, outre les recherches que nous venons de présenter, sa célèbre avancée sur le Grand Théorème de Fermat. Son lancement aura mieu le 18 Mars 2016, dans le cadre d'une journée commémorative (voir le communiqué de presse) à l'Institut Henri Poincaré (Paris).
My Favourite Things... (Clarinette ou Sax Soprano?)
 |
Clin
d'œil du Mathouriste à
destination... de lui-même, ce
titre évoque, bien sûr, la petite chanson
gentiment
niaise de la comédie musicale (1959) de Rogers &
Hammerstein, La
Mélodie du Bonheur (The Sound of Music),
que sussure Julie Andrews dans le film (1965). Mais, dès
1961, John
Coltrane s'est emparé de cette rengaine et ne la
lâchera plus, en
offrant des versions de plus en plus longues, habitées d'une
transe incantatoire (voir cette version
de 1965,
en Belgique). Le morceau sans doute le plus emblématique du
sax soprano
avec le Summertime
de Bechet (à qui, en dépit de l'écart
de génération
et de style, Coltrane a payé son tribut: Blues to Bechet).
Bref, Now is the Time
de revenir à la comparaison promise: clarinette/soprano.
Capture d'écran de la vidéo proposée. |
Alors, avez-vous trouvé la différence importante entre ces deux instruments? Sans doute la première que l'on relèvera est la matière: ébène contre métal. Mais ce n'est pas la plus pertinente, et un exemple expérimental célèbre est là pour nous le rappeler: lors du fameux concert au Massey Hall de Toronto en 1953, Charlie Parker utilise un saxophone alto en plastique blanc; la sonorité, quoique légèrement différente (moins "chaude", serait-on tenté de dire) reste parfaitement identifiable comme celle d'un alto, sans risque d'erreur! Testez vous même sur... Night in Tunisia, on ne s'en lasse décidément pas! Il n'y a plus qu'à remercier la marque suédoise qui lui avait confié ce modèle pour essai (et tant pis pour la belle légende qui voudrait qu'ayant mis son Selmer au clou pour se procurer sa dose d'héroïne, Parker n'avait pu trouver à louer que celui-là dans toute la ville...)
La différence essentielle, quelques calculs -un peu plus "relevés"- vont le montrer, est dans la forme de l'instrument: quasi cylindrique pour la clarinette, conique pour le saxophone.
| C'est un retour à un modèle unidimensionnel en coordonnées spatiales: seule compte l'abcisse x le long de l'axe de l'instrument, et l'aire S(x) de la section du tube à cette abcisse. Par contre, l'onde est longitudinale -c'est à dire, dans la direction du tuyau, contriarement au cas de la corde où elle était transversale (perpendiculairement à la corde). Elle est caractérisée par deux fonctions: * p (x, t) : surpression de l'air au point x, au temps t; * u (x, t) : vitesse d'une particule d'air au point x, au temps t; Deux fonctions inconnues, mauvaise nouvelle... mais la bonne, c'est que nous avons deux équations pour les déterminer! ρ (x, t) désigne la masse volumique moyenne de l'air, ρ0 sa valeur moyenne. |
 |
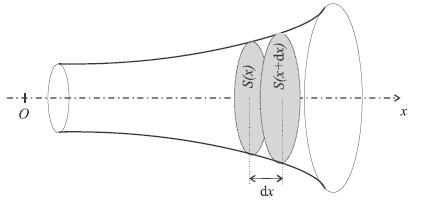Les deux équations traduisent la conservation de la masse, d'une part, et les lois fondamentales de la dynamique appliquées aux "fluides parfaits", d'autre part. Cette deuxième relation, dite équation d'Euler des fluides parfaits, s'écrit
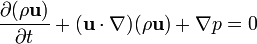
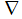désignant, selon l'habitude, le vecteur gradient. Mais comme u est petit, le deuxième terme est (souvent) très petit, ce qui invite à se débarasser providentiellement de ce terme aussi gênant que non linéaire:
on ne fait pas de bonne physique sans approximations. En outre, il n'y
a qu'une coordonnée d'espace, et de vectorielle
l'équation devient scalaire | conservation de la masse |  |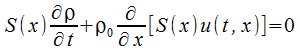
| Euler, linéarisée |  |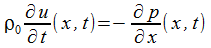
Quelques considérations de physique relatives à ρ et le report de l'une dans l'autre permettent d'obtenir les équations vérifiées par la pression d'une part, la vitesse d'autre part, avec lesquelles nous pouvons travailler:
| pression |  |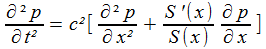
| vitesse |  |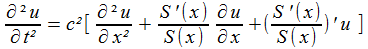
La Clarinette
Elle est cylindrique, donc S(x) est constante, et S'(x) = 0. Chacune de nos deux fonctions inconnues vérifie donc... la même équation que celle des cordes vibrantes!| pression |  |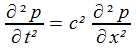
| vitesse |  |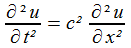
Aucun sorcier n'a (d'un coup de saxophone magique?) transformé la clarinette en guitare, ni les vibrations transversales en vibrations longitudinales: tout simplement, le même modèle mathématique s'applique à deux situations physiques différentes. Ce qui justifie, en quelque sorte, l'utilité de mathématiciens et les menus émoluments liés à leur gagne-pain.
S'y ajoutent deux conditions aux limites typiques de l'acoustique:
- le tube est (presque!) fermé à l'extrémité du bec de l'instrument; donc la vitesse s'y annule : u (0, t) = 0;
- le tube est ouvert à l'extrémité du pavillon de l'instrument; la surpression y est donc nulle: p (L, t) = 0;
u (x, t) = g(x) . h(t)
on obtiendra deux équations différentielles ordinaires, à coefficients constants:g" (x) + k² g (x) = 0 , h" (t) + ω² h (t) = 0 , k = ω / c
La condition à la limite x=0 conduit à g (x) = sin kx, et les solutions élémentaires sont de la forme
u (x, t) = sin(kx) . sin (ωt) ou u (x, t) = sin(kx) . cos(ωt)
Mais si la pression a une forme
similaire, il ne faut pas oublier que les deux sont liées entre
elles par l'équation d'Euler linéarisée. Par
suite, on a, dans le cas de la première forme (la
deuxième se traiterait de même et n'apporterait rien de
neuf)
u (x, t) = sin(kx) . sin (ωt) et p (x, t) = ρ0. c. cos(kx) . cos(ωt)
La condition à la limite x=L va restreindre à une famille bien particulière de k, et donc de ω, qui sont des pulsations propres.
cos(kL) =0 soit kL = (m+1/2).π
| ωm = (2m+1)πc / 2L ; m entier. |
La fréquence fondamentale d'une note de la clarinette étant f0 = ω0 / 2π = c / 4L
sa première harmonique est f1 = ω1 / 2π = 3c / 4L =3f0 , et ainsi de suite...
sa première harmonique est f1 = ω1 / 2π = 3c / 4L =3f0 , et ainsi de suite...
Seules les harmoniques impaires de la note émise sont présentes.
Le Soprano
L'instrument est un cône de demi-angle au sommet α ; à l'abcisse x, sa section est un disque de rayon proportionnel à x:rx = x.tan α , d'où S(x) = a x²
et l'équation de la pression devient
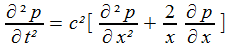
C'est presque la même équation aux dérivées partielles que celle qu'a rencontré Fourier en étudiant la chaleur dans la sphère: une dérivée temporelle seconde remplace la dérivée temporelle première. Une fois de plus, on sépare les variables
L'équation à l'inconnue g est inchangée, tandis que celle qui porte sur h passe du premier au second ordre, et remplace donc une exponentielle décroissante par une oscillation sinusoïdale. La première a été résolue... en lisant Fourier, par le changement de fonction g1(x) = x g(x). De nouveau, le même modèle mathématique s'applique à deux situations physiques différentes, pour notre plus grande économie!
D'où les solutions correspondant à des modes propres:
p (x, t) = g(x) . h(t)
| en t | h" (t) + ω² h (t) = 0 |
| en x | xg"(x) +2 g'(x) + k² x g(x) = 0 , k = ω / c |
| au bord | p (L, t) = 0 soit g(L) = 0 |
L'équation à l'inconnue g est inchangée, tandis que celle qui porte sur h passe du premier au second ordre, et remplace donc une exponentielle décroissante par une oscillation sinusoïdale. La première a été résolue... en lisant Fourier, par le changement de fonction g1(x) = x g(x). De nouveau, le même modèle mathématique s'applique à deux situations physiques différentes, pour notre plus grande économie!
D'où les solutions correspondant à des modes propres:
p (x, t) = cos(ωt) . sin(kx) / x
sin(kL) = 0 soit kL = (m + 1)π
sin(kL) = 0 soit kL = (m + 1)π
| ωm = (m+1)πc / L ; m entier. |
La fréquence fondamentale d'une note du sax soprano étant f0 = ω0 / 2π = c / L
sa première harmonique est f1 = ω1 / 2π = 2c / 2L =2f0 , et ainsi de suite...
sa première harmonique est f1 = ω1 / 2π = 2c / 2L =2f0 , et ainsi de suite...
Toutes les harmoniques paires et impaires de la note émise sont présentes ...
... contrairement au cas de la clarinette, qui n'a que les harmoniques impaires!
... contrairement au cas de la clarinette, qui n'a que les harmoniques impaires!
 |
 |
De manière plus musicale (et moins aride), admirez les différences de sonorité qui font que ces jazzmen, sur le même instrument, le saxophone alto, sont identifiables dès les deux ou trois premières notes:
L'alto est un choix amoureux du Mathouriste, mais la théorie reste la même: la forme courbée, nécessaire pour allonger le tube, n'a pas d'incidence en première approximation. Cela devrait vous convaincre qu'il reste encore beaucoup de secrets hors de la théorie précédente... Ceci dit, si quelque lecteur bien outillé peut nous fournir les spectrogrammes correspondants, nous nous ferons un plaisir de les publier!
Et du côté des Cuivres...
Une différence similaire apparaît entre la trompette, instrument essentiellement cylindrique (l'évasement final du pavillon peut être négligé) et son "cousin du pauvre" -il fut l'instrument des Noirs Américains aux débuts du jazz-, le cornet (à pistons), dont le tuyau est considéré comme conique. C'est encore plus net avec le bugle (flugelhorn), conique lui aussi, au son plus mat, plus velouté. Le mécanisme de production du son est le même pour les trois instruments, une embouchure (c'était une anche vibrante pour clarinette et saxophone), donc leur différence de son vient de la composition du spectre en harmoniques différents, qu'explique la forme du tuyau, comme dans le cas des instruments à anches. Le facétieux (mais toujours excellent) trompettiste ellingtonien Clark Terry en fit une brillante démonstration lors d'une belle et chaude soirée niçoise, alternant en bouche les deux instruments; la différence de forme est flagrante. |
 |
| Clark Terry, bugle dans la main droite, trompette dans la gauche! (Nice, Arènes de Cimiez, 13/07/90, 23h) | |
Pour vous faire une idée de la différence de son, c'est deux albums mythiques de Miles Davis que le Mathouriste vous recommande, dans le somptueux écrin des orchestrations de Gil Evans: Sketches of Spain à la trompette, Miles ahead au bugle.
Quelques Applications Modernes de la Recherche des Modes Propres...
Si la musique qui nous a servi d'illustration était du XXème siècle, la physique et les mathématiques utilisées dataient indiscutablement du XIXème ... L'élégante simplicité de la recherche de modes propres est-elle encore d'actualité dans la science récente?La réponse est oui... en trois exemples (les titres sont là pour vous allécher). L'aventure continue dans la page suivante!
Niveaux d'Énergie de l'Atome d'Hydrogène
Chaos en Météo: le Système de Lorentz
Héliosismologie, Ondes Gravitationnelles
(à
suivre...)
Références Spécifiques à cette Page
- Dave BENSON, Music: a Mathematical Offering (version en ligne, 2008)
- Dave BENSON, Music: a Mathematical Offering (Cambridge University Press); page web du livre.
- A. CHAIGNE, Les Instruments de Percussion
- B. FABRE, instruments à vent à trous latéraux (flûte, clarinette)
- C. GABRIEL, Cours d'Acoustique (téléchargeable par chapitres), ,notamment chap 4 (instruments) et chap. 11 (acoustique musicale et gammmes)
- B. GOODWINE, Engineering Differential Equations: Theory and Applications (Springer)
- Cours du Groupe Spécialisé d'Acoustique Musicale
- Liens du Groupe Spécialisé d'Acoustique Musicale
- H. HELMHOLTZ, Théorie Physiologique de la Musique (Masson)
- J.-C. PASCAL, Vibrations et Acoustique, Cours à l'ENSIM du Mans (2009)
- Lord RAYLEIGH, The Theory of Sound (Dover): en ligne: vol 1 , vol 2
- B.H. SUITS, Physics of Music, Notes (cours en ligne)
- Théorie d'Euler-Bernoulli: Poutres en Vibration sur Wikipedia
- O. THOMAS, Vibrations non Linéraires, Application aux Instruments à Percussion (Thèse)
Poursuivre...
Revenir à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Aller à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Aller à la Page: Naissance de la Transformée de Fourier (Promenade dans la Théorie Analytique, #3)
Aller à la Page: Naissance de la FFT: Fast and Fourier ! (Promenade dans... la suite de l'histoire, #4.1)
Aller à la Page: Signaux, Transformées... et Applications (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique