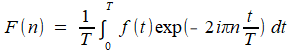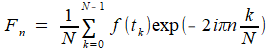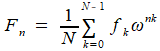Signaux: Fast and Fourier!
... Une Promenade Fouriériste! (Partie 4.1)
Cela peut surpendre à bon droit, mais c'est ainsi: la transformation intégrale de Fourier, qui adapte au cas NON périodique une technique de superposition de composantes périodiques, va être, plus encore que sa série, la clef du succès contemporain des outils de Fourier. Voici d'ailleurs un avis autorisé:
| "Et
l'analyse de Fourier sert à tout: à analyser les
sons et à les graver
sur un CD, mais aussi à analyser les images et à
les transmettre par
Internet, ou à analyser les variations du niveau de la mer
et à prédire les marées...
[...] Et ce qui est sûr, c'est que -avec tout le respect
dû à
l'écrivain surdoué dont j'ai
dévoré les œuvres quand
j'étais enfant-
l'influence de Joseph Fourier est maintenant bien plus importante
que
celle de Hugo lui-même; son "grand poème
mathématique" (comme disait
Lord Kelvin), est utilisé chaque jour par des milliards d'humains qui ne s'en rendent
même pas compte." C. Villani, Théorème
Vivant (Grasset,
2012)
|
|
Comment
faisons-nous pour qu'il en soit ainsi, que nous soyons tout
à
la fois acteurs de cet emploi inconscient et responsables de la place
qui en résulte pour Fourier, celle d'inconnu le
plus célèbre?
C'est ce que nous allons essauer d'expliquer ici. Une grande partie de
l'explication tient dans le rôle que joue la
transformation
de Fourier en imagerie numérique... c'est
déjà
dire combien notre Joseph est en
avance sur son temps: presque deux siècles!
 Une icône
de l'imagerie, le mannequin Lena... et sa transformée de
Fourier.
|
 attention tout de même
à ne pas abuser...
(cartoon trouvé sur ce site) |
La Transformée de Fourier, qu'est-ce que c'est?
Vous n'êtes pas obligé, pour lire ce qui suit, d'avoir fait avec nous la portion correspondante de la promenade dans la Théorie Analytique de la Chaleur; voici donc un petit résumé du passage du cas périodique (série) au cas NON-périodique (intégrale).< à
venir>
La Transformée de Fourier, est-ce que ça peut se faire discrètement?
La Transformée de Fourier Discrète (TFD) est une approximation de la "vraie" transformée en vue du calcul numérique effectif; elle consiste en deux étapes qui faussent un peu (mais pas trop, du moins l'espère-t-on) sa valeur. En fait, on "revient en arrière" par rapport à la démarche de Fourier, en considérant l'intégrale sur une "grande" période, et en l'apporchant par une somme finie!Caricaturons à peine:
- Le grand progrès du Calcul Infinitésimal, c'est le passage du discret au continu (donc de la somme finie à l'intégrale);
- le grand progrès du calcul informatisé, c'est... l'inverse!
|
Lorsqu'on approche
l'aire que
représente l'intégrale d'une fonction
réeelle par la somme des aires
des trapèzes (voir cette page) correspondant
à une subdivision régulière de pas h (la hauteur des
trapèzes), la valeur approchée est
h { [g(a) + g(b)]/2 + g(x1)
+ g(x2) + ... + g(xn-1) }
car les valeurs
intermédiaires g(x1)
apparaissent deux fois,
étant bases de deux trapèzes.
Le cas périodique est encore plus agréable, puisque f(a) = f(b), on a alors (avec a = x0) h { g(x0)
+ g(x1)
+ g(x2) + ... + g(xn-1) }
Appliquons cette approximation aux coefficients de Fourier sur une
grande période T,
qu'on découpe en N
morceaux: h=T/NAvec tk = kh, fk = f(tk) et ω = exp (-2iπ / N) la racine Nième fondamentale de l'unité |
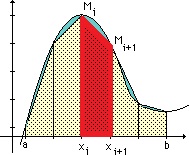 un trapèze a pour
aire
h [ g(xi) + g(xi+1)] / 2 |
|||||
Contrairement à ce que leur nom pourrait laisser croire, les nombres complexes simplifient la tâche et les formules! D'abord, selon nk modulo N, ωnk ne prend que N valeurs ωr(nk) qu'il est facile de précalculer et stocker, ce qui évitera de très nombreuses répétitions du calcul de puissances. On n'aura donc à faire, dans chaque ligne, N multiplications seulement, soit N² en tout. Ce qui
malheureusement, reste beaucoup, pour ne pas dire beaucoup trop!
Si l'on traite une image, N
est le nombre de pixels, par exemple, 106 pour
une image 1000x1000. N²
vaut alors 1012
. Cela fait beaucoup de multiplications (et tout ça, pour
rendre
méconnaissable notre amie Lena, vous indignerez vous...
patience!); c'était carrément trop pour un calcul
en
temps raisonnable dans les années 1960-d'ailleurs,
à cette époque, le traitement de
l'image nexistait pas! Il y avait cependant une demande
réelle dans d'autres domaines; voici un exemple:
Par contre, la merveilleuse formule d'inversion entre f et sa transformée de Fourier F demeure vraie: il suffit d'intervertir f et F,et de changer ω en son conjugué. (Daccord, faire gaffe au N baladeur...bon, trois fois rien: pour un informaticien, c'est le même calcul!) |
||||||
La Transformée de Fourier, est-ce que ça peut se faire rapidement?
On aura donc compris que, pour que la transformation de Fourier se rende utile, il faut accélérer le calcul précédent, qu'on a réduit à des opérations très simples à programmer dans un calculateur... mais trop nombreuses.À la question précédente, nous pouvons fièrement répondre
OUI !!!!!
... mais pas depuis si longtemps que ça! L'article qui va
bouleverser le monde du calcul (disponible intégralement en ligne)
parait en 1965; il est dû à deux
Américains: James W. Cooley (1926-2016) |
 |
 John W. Tukey (1915-2000) |
2N log2N au lieu de N²
Pour bien comprendre le gain réalisé, il ne faut savoir qu'une chose du logarithme: il représente, en gros, le nombre de chiffres avec lequel on écrit un nombre: un nombre entre 100 et 999 a un logarithme décimal qui vaut 2,***...;entre 1000 et 9999, il vaut 3,***..., etc... Celui de base 2 représente de façon similaire le nombre de chiffres en base 2, qui reste proportionnel au précédent. En pratique, on peut donc considérer le nombre d'opérations à réaliser comme inférieur à C.N, où C est une constante (N dépassera rarement 30 chiffres, par exemple), au lieu de N²; autrement dit, on a gagné un ordre de grandeur. Le gain est donc énorme! On peut le visualiser concrètement sur un échiquier ayant N cases de côté: l'algorithme naïf fait autant de produits que le nombre de cases de l'échiquier, tandis que l'algorithme de Cooley et Tukey ne requiert que quelques rangées. Ci contre, N = 8 est très petit (par rapport aux usages envisagés), mais déjà le gain est remarquable. On l'a donc baptisé Transformation de Fourier Rapide (TFR), ou, selon la dénomination internationalement en vigueur, Fast Fourier Transform (FFT) |
 |
| FFT, explication... rapide? Regardons d'abord le cas N = 4.
Ici, ω = i, ω = -1, et les formules deviennent (en omettant le facteur 1/ N)
Dans le deuxième tableau, on a réordonné pour ne pas calculer plusieurs fois, ni les mêmes sommes, ni les mêmes produits. On est passé, de manière évidente, de 4 produits à 2, et, en regardant mieux encore, à un seul: i affecte deux fois la même quantité! On calculera donc le "paquet" ( f1 - f3 ), puis une seule fois le produit i(f1 - f3 ), à ajouter à l'un des termes, retrancher à l'autre. Observons mieux encore: on a séparé les fk selon les indices pairs et impairs, fait deux fois le même calcul , sur deux paquets de données distincts (f0, f2) et (f1, f3), et réassemblé.
Et dans le cas général? Principe: quand c'est bon... on
recommence! ("Play it again, Sam!" vous dirait Woody
Allen...)
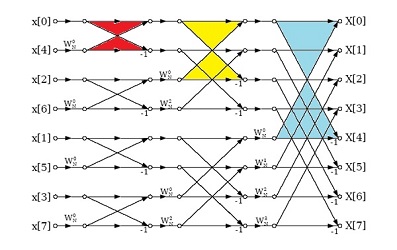
Pour N=8, on peut encore séparer en indices pairs et impairs, faire un calcul séparé, et réassembler; et de façon similaire ramener le cas N=2m à deux calculs sur des données de taille (le nombre d'indices) m, puis un réassemblage. Le succès tient à ce que ωm = -1 ; ωm + r = -ω r (
r entre
0 et m-1)
Il
suffit de prendre pour N une
puissance de 2 -les informaticiens aiment ça, c'est connu!-
et
le procédé peut être
itéré jusqu'au
cas le plus trivial, que nous venons de regarder en détails.
C'est la réitération qui fait l'efficacité du calcul: faire ceci une seule fois ne serait qu'une piètre économie. Lorsqu'on découpe le calcul sur 2q valeurs en deux calculs sur 2q-1 valeurs et un réassemblage, le coût en opérations (+ et x) s'établit à: c(q) = 2 c(q-1) + c(réassemblage)
c(q) = 2 c(q-1) + 3. 2q-1 car on doit faire un
produit et deux
sommes (i.I1,
±I0, ±iI1 dans
le cas exhibé) sur 2q-1 données
(q-1 valait
2 dans le cas exhibé)
. Cette équation de récurrence se résout aussi facilement que l'équation différentielle y' = 2y+3 exp (2x), soit dit pour ceux qui sont plus familiarisés avec ce deuxième exercice! Comme 2q est solution de la récurrence "sans second membre" c(q) = 2 c(q-1) , on pose c(q) = 2q d(q), et l'on obtient une solution particulière de type A 2qq ; A 2mm = A
N log2N
Toujours plus fort, toujours plus hard: si c'est pré-câblé, c'est encore plus rapide... et c'est pourquoi les concepteurs de circuits ont fabriqué des circuits dédiés, qui effectuent directement la reconstruction à partir du cas de deux; à la première étape, ce sont deux entrées distantes de N/2 qui doivent d'abord être combinées. |
Cooley et Tukey ont raconté l'histoire de leur découverte dans un nouvel article à quatre mains, qui révèle le contexte et toute la puissance que l'on pouvait attendre de ce procédé:
| "Lors
d'une réunion du Comité de Conseil Scientifique
du
Président Kennedy, en 1963, Dick Garwin (de l'I.B.M. Watson
Research Center,N.Y.) remarqua que John Tukey, assis à
côté de lui, gribouillait*, comme à son
habitude,
sur son bloc note; il jetait sur la page des formule de
transformées de Fourier, un sujet auquel
s'intéressait
Dick. En réponse à une question de ce dernier, il
lui dit
qu'il travaillait
à l'amélioration de l'algorithme de calcul de la
transformation de Fourier discrète [...] En fait, Dick était bien au fait du grand besoin d'un tel algorithme dans un vaste champ d'applications, et nourrissait de grands espoirs à ce sujet. Il fut révélé plus tard que Dick en avait pris conscience en travaillant sur un traité d'interdiction des essais nucléaires. Comme il n'était pas question que la Russie accepte, à cette époque, une inspection de ses sites, Dick étudiait la faisabilité d'une détection d'explosion nucléaire au moyen d'analyses spectrales des données provenant de sismographes. Il comprit que l'obstacle principal était le volume de calcul des transformées de Fourier qu'il faudrait effectuer." J.Cooley, J.Tukey , On the Origin and Publication
of the FFT Paper
(1993)
*John Tukey, who sat next to him,
was, in usual way, doodling
with a notepad...
|
Et si vour regardiez les Manhattan
Transfer en action?
Ou encore, la version du jeune
Kurt Elling avec, à 3' du début:"I feel so lost without my
doodlin'
Doodlin really helps me in my
mind! "
|
On réunit des mathématiciens et des juristes pour savoir s'il fallait breveter l'algorithme; à cette occasion on fit quelques recherches d'antériorité des idées. L'article mentionnait d'ailleurs, dès sa prmeière ligne, le statisticien F. Yates, en 1937.
| "
La «méthode du doublement»
était apparue dans
de nombreuses publications antérieures. Herman Goldstine
trouva
la plus ancienne référence connue dans un obscur
article
de C.F. Gauss, qui n'avait jamais été traduit du
latin. Il inspira à M.T. Heideman, D.H. Johnson, et
C.S.Burrus un article
fouillé sur l'histoire de la FFT" J.Cooley, J.Tukey , On the Origin and Publication
of the FFT Paper
(1993)
|
 Gauss et les astéroïdes... (source: site de Jeff Miller) |
| Il s'agissait d'un
calcul
d'interpolation relatif
à l'astéroïde Pallas. Gauss veut
modéliser sa trajectoire par une formule donnant la déclinaison
en fonction de l'ascension
droite (angles de repérage usuels en
astronomie) de la petite planète; disposant de 12
données, Gauss les avait
regroupées en 3 séries de
4; et déterminé
pour chacune les valeurs des coefficients
d'une expression de la forme p + q cos x + r sin x + s cos 2x + t sin 2x
Chaque
série donnait,
comme on peut s'y attendre, des valeurs différentes de sa
voisine, l'orbite n'ayant aucune raison de suivre une formule aussi
férocement tronquée...Puis il
considérait p,
q,
r et
s eux mêmes
comme des expressions de la forme
u + v cos 4x
+ w sin 4x
pour
tirer un développement approché
jusqu'à l'arc 6x
. Ainsi , il avait effectué à partir de 12 = 3x4, trois calculs, chacun sur le tiers des données, réassemblés ensuite: le principe d"économie appliqué au calcul manuel est le même que celui de la FFT, et Gauss envisage un produit de deux nombres quelconques. La seule différence est qu'il ne réitère pas; il n'y a qu'une seule étape! |
|
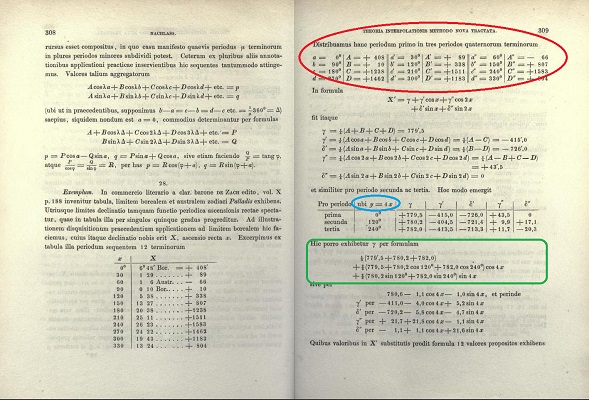
| L'article n'a été publié qu'après sa mort, mais il est logique de penser qu'il est contemporain de ses travaux sur Pallas, au vu de l'exemple choisi, de son journal et de sa correspondance. Il a dû par conséquent être écrit vers 1805! | |
 |
 |
le calcul de Gauss (Œuvres, t.3, pp308-310) |
|
La lecture commentée d'Herman Goldtsine figure dans son livre A History of Numerical Analysis from the 16th through the 19th Century, pp 251-253 (les deux premières, soit l'essentiel de son commentaire, sont consultables en ligne ici).
Voici deux avis choisis pour leur pertinence et leur profondeur.
|
Une fois bien
établie, il devint
clair que la FFT avait une longue et intéressante histoire,
qui
remontait jusqu'à Gauss. Mais avant l'avènement des
ordinateurs,
c'était une solution à la recherche d'un
problème! Les mathématiques,
sans doute plus encore que toute autre entreprise humaine, sont
parsemées d'idées nées en
dehors de leur époque. (Considérez, par
exemple, le travail de Fourier sur la programmation linéaire
-un sujet
dont l'utilité dépend de l'existence
d'ordinateurs, ou la découverte
par Wilbraham du phénomène de Gibbs)
T. KÖRNER,
Fourier
Analysis (1988)
|
| "De nos jours, qu'il y ait eu un
temps avant la technologie numérique est au delà
de l'imaginable (au moins pour beaucoup de mes étudiants).
Presque chacun sait que, d'une certaine manière, toutes les
données qui circulent sur Internet, à travers nos
modems et nos téléphones cellulaires, ne sont que
des suites de 0 et de 1 qui donnent au monde, comme par magie, la
grande vitesse qui le caractérise aujourd'hui. Beaucoup de
cette magie vient d'une famille d'algorithmes à qui l'on a
donné le nom de "Fast Fourier Transform", FFT pour les
intimes, dont la version publiée par
Cooley et
Tukey est la plus célèbre. Et vraiment,
la FFT est probablement l'algorithme
dont l'ubiquité est la
plus évidente dans l'analyse et le traitement
des
données discrètes.". D.
ROCKMORE, The
FFT: An Algorithm the Whole
Family Can Use (2000)
|
Les deux autres idées trop en avance sur leur temps citées dans le premier sont, l'une de Fourier lui-même (totalement en dehors de sa Théorie Analytique, ce qui est particulièrement remarquable de sa part, l'autre liée à la théorie des séries de Fourier... pour laquelle un ordinateur aurait été d'un grand secours!
Et pourtant, quand on y réfléchit, en 1830, à la mort de Fourier, tout est presque là: sa théorie, l'idée algorithmique de Gauss, et... l'ordinateur de Babbage et Ada Lovelace, en phase de conception (complète en 1840), qui ne sera malheureusement jamais construit!
Une belle unanimité s'est faite autour de son inclusion dans un Top Ten des Algorithmes; au tournant du troisième millénaire:
Lire la
liste entière,
présentée par Barry Cipra
Passons à la Pratique!
 |
 |
Si l'algorithme est dans le Top 10, c'est, vous vous en doutez bien,
que les applications sont nombreuses; vous les trouverez donc dans des
pages qui leur sont spécialement dédiées. Contentons nous ici d'une
séquence délicieusement vintage, celle où Hewlett-Packard, qui
fabriquait déjà des analyseurs de Fourier électroniques, commercialisa
une nouvelle machine, la HP5451A (1972), pouvant intégrer une unité
supplémentaire dédiée à la FFT. Laquelle permet de "réduire à 15ms le calcul des fréquences d''un jeu de 1024 données, contre 1,5s au seul 5451A", temps lui-même présenté comme une nette amélioration par rapport aux modèles antérieurs.
Et si vous êtes tenté, la notice de la machine est toujours disponible en ligne! |
|
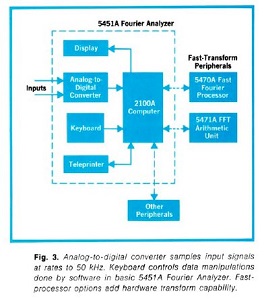
| Le schéma ci-dessous met bien évidence l'un ou l'autre des modules additionnels | |||
Des images ci-dessus, celle de gauche est tirée d'un article de présentation New Capabilities in Digital Low Frequency Spectrum Analysis
et la montre en compagnie des chefs de projets responsables de
limplémentation de la FFT. Celle de droite est... une image de
promotion commerciale! (mais... comment croyez-vous qu'on présentait
une voiture de luxe à la même époque?)
En tout cas, Fourier y est clairement montré à son avantage, et ne
manquez pas de l'agrandir, car ce que vous pourriez prendre pour des
franges de la robe est une phrase tout à fait sympathique.
|
 |
||
Pour ne pas trop allonger cette page, vous en trouverez la suite dans chacune des deux pages suivantes, dont seul figure ici le sommaire. Mais la liste est loin d'être complète!
-
Traitement du Signal
-
Parole et... Musique!
-
Qui n'a jamais fait une photo au format JPEG?
-
Qu'est ce qui rend un scanner médical (ou une IRM) performant?
-
Applications Optiques
-
Des cristaux aux quasi-cristaux
-
Naissance de "l'Optique de Fourier"
-
Tout ce que vous voulez savoir sur les étoiles... sans y avoir jamais mis le pied!
Références
- S. CLINE, N. MARSCHKE, New Capabilities in Digital Low Frequency Spectrum Analysis (HP Journal, Juin 1972, vol.23 n°10)
- J. COOLEY, The Re-Discovery of the Fast FourierTransform Algorithm (Mikrochimica Acta, 1988)
- J. COOLEY, J.TUKEY , On the Origin and Publication of the FFT Paper (1993)
- J.R. DELLER, Tom, Dick, and Mary Discover the DFT ( IEEE Signal Processing Magazine, Avril 1994)
- M. HEIDEMAN, D. JOHNSON, C. BURRUS, Gauss and the History of the Fast Fourier Transform ( IEEE ASSP Magazine, Avril 1994)
- D. ROCKMORE, The FFT: An Algorithm the Whole Family Can Use (Computing in Science & Engineering, 2000, IEEE)
- J.L. ROCH, La Transformée de Fourier en Algorithmique: Discrète et Efficace (LIG/INRIA Grenoble)
- P. Flandrin, Des signaux partout. Des chauves-souris à Internet, conférence à l’Académie des sciences (2020, disponible en ligne)
- P. Flandrin, Signal, représentation et modélisation, conférence à l’Université de Lyon (2020, disponible en ligne)
- E. BRIGHAM, The Fast Fourier Transform and its Applications (Prentice Hall)
- B. ESCUDIE, C. GAZANHES, H. TACHOIRE, V. TORRA, Des Cordes aux Ondelettes (Presses de l'Université de Provence)
- H; GOLDSTINE, A History of Numerical Analysis from the 16th through the 19th Century (Spinger)
Poursuivre...
Aller à la Page: Analyse Harmonique... mais Pourquoi ce Nom? (Prélude à la Théorie Analytique, #0.1)
Aller à la Page: Analyse Harmonique... en tambours et clarinettes (Prélude à la Théorie Analytique, #0.2)
Revenir à la Page: Naissance des Séries de Fourier (Promenade dans la Théorie Analytique, #1)
Revenir à la Page: l'Armille, la Sphère, le Cylindre et les Autres... (Promenade dans la Théorie Analytique, #2)
Revenir à la Page: Naissance de la Transformation de Fourier (Promenade dans la Théorie Analytique, #3)
Aller à la Page: Signaux, Transformées... et Applications pratiques (Promenade dans... la suite de l'histoire, #4.2)
Aller à la Page: Cristallographie, Optique, Spectroscopie... (Promenade dans... la suite de l'histoire, #4.3a)
Aller à la Page: Spectroscopie par FFT en exploration spatiale (Promenade dans... la suite de l'histoire, #4.3b)
Aller à la Page: Brève Histoire des Séries Trigonométriques (Promenade dans... la suite de l'histoire, #4.4)
Aller à la Page: De Gabor aux Ondelettes (Promenade dans... la suite de l'histoire, #5)
Aller à la Page: De Pythagore à Parseval (Promenade dans... la suite de l'histoire, #6)
Aller à la Page: du Refroidissement de la Terre à l'Effet de Serre (En lisant les Mémoires de 1824 et 1827)
Aller à la Page: Kelvin, l'Analyse de Fourier et les Marées (En bord de mer...avec de Belles Mécaniques!)
Aller à la Page: Séries de Fourier et Modes Propres, Applications Modernes (Pré/postlude à la Théorie Analytique, #0.3)
Aller à la Page: Fourier, père de l'Optimisation Linéaire (Promenade dansles sommets... avec Giacometti!)
Aller à la Page: Fourier, Théoricien des Nombres (e est irrationnel... sa VRAIE preuve !)
Aller à la Page: Hommage à Jean-Pierre Kahane (une vie pour Fourier...)
Revenir à la Page Biographique