|
Il est particulièrement
intéressant d'observer Bologne de haut, histoire "d'y revoir un jour sa pincée de tuiles", comme
disait Nougaro de Toulouse. Mais ici, point besoin d'avion ou de
drone, il suffit de prendre son courage à deux jambes et de faire
l'ascension de sa plus haute (97,2m) et plus célèbre maison-tour, la
tour Asinelli. Elle n'est en rien hors sujet dans une page consacrée à
l'histoire des sciences, puisque le jésuite Riccioli -dont nous
reparlerons plus loin- prit avantage de son inclinaison pour y faire,
en 1640, des expériences sur la chute des corps, comme Galilée avant
lui au campanile de Pise, une bonne cinquantaine d'années auparavant
(si du moins c'est la vérité historique, et ,non, comme on le soupçonne
de plus en plus, une belle légende inventée par son disciple Viviani,
biographe assurément, hagiographe probablement).
|
Les tours Asinelli (la plus haute) et Garisenda |
|
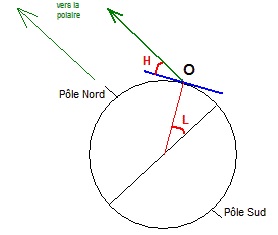 |
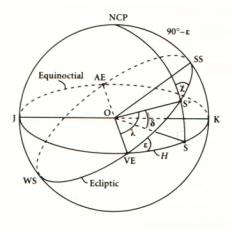
Et encore mieux si l'on s'en tient au héros de cette page: Cassini y grimpa pour mesurer la hauteur sur l'horizon de l'étoile polaire, moyen commode et relativement précis d'obtenir la latitude du lieu -tout simplement grâce à l'égalité de deux angles à côtés perpendiculaires. Il faut seulement que l'étoile et l'horizon soient apparents, ce qui impose d'effectuer l'opération à l'aube ou au crépuscule, et mieux aux deux, si l'on veut être plus précis en réalisant la moyenne des deux observations; séparées de 12h, elles ne peuvent donc être réalisées qu'en hiver. Cassini trouva 44°30'22", information utile à la détermination, à l'aide de sa méridienne, de l'obliquité de l'écliptique. figure empruntée à ce site, où vous découvrirez plus en détails les corrections fines à effectuer, en particulier parce que l'étoile polaire n'est pas exactement au pôle ord céleste, et donc semble décrire un petit cercle autour de lui.... |
|
|
La vue est superbe dans
toutes les directions, et si les autres tours
de la ville attirent l'attention dans la direction verticale, l'élément
qui semble
dominer la cité, par sa masse et l'ampleur
de ses dimensions, est la
basilique San Petronio, édifice d'un gothique tardif flirtant avec la
renaissance (début des travaux: 1390), édifice inachevé aussi, dont ni
le transept, ni le dôme
prévus ne furent réalisés, dont le clocher est... provisoire, et la
façade à moitié seulement couverte de marbre!
|
||
C'est de cette vaste
basilique que Cassini a fait un observatoire astronomique géant!
Plus précisément, il y a construit la plus grande méridienne du monde, qu'il préférait nommer héliomètre, puisque cela devait lui permettre de réaliser des mesures précises, liées à la trajectoire apparente du soleil tout au long de l'année.
Découvrir l'Instrument
Revenons à notre vue "aérienne" depuis la tour Asinelli; armé d'un bon zoom, il est facile de repérer son emplacement dans le toit, au niveau de la quatrième travée -ce que nous confirmera le plan de la basilique, un peu plus bas.
 |
Son rôle est exactement le même que celui du diaphragme d'un
appareil photo, faisant de la cathédrale une camera obscura (dont le
principe, faut-il le rappeler, remonte à Aristote ). L'image à capturer
est celle du disque solaire (contour apparent de la sphère solaire, tel
qu'on peut l'observer sans danger par un ciel hivernal légèrement
voilé, ou encore, au lever et au coucher). Imaginons, pour simplifier,
que ce trou est réduit à un point mathématique: c'est une bonne
approximation qui nous débarasse des questions de pénombre (et qui,
dans le cas d'un appareil photo, rendrait toute l'image nette, car nous
savons bien que plus le trou du diaphragme est grand, plus la zone
floue sera importante). Les rayons solaires forment alors un cône,
de base le disque solaire, et de sommet le trou. Le sol de
la basilique est un plan, qui coupe ce cône suivant... une conique,
conformément à la théorie d'Apollonius de Pergé, et plus précisément
une ellipse.
Voilà donc la ligne et l'oculus présentés séparément... et maintenant, il va falloir les faire trvailler ensemble! |
En un jour, la terre tourne sur elle-même, ce qui se traduit par un mouvement apparent du soleil en un cercle centré sur la terre (en négligeant pour la bonne cause le petit déplacement de la terre sur son orbite, pendant cette même journée...) On a observé, dès l'antiquité, que l'ombre d'un bâton vertical fiché en terre est la plus courte au moment où le soleil est le plus haut , à son point de culmination (attention, ce n'est pas le zénith -en tout cas, pas sous nos latitudes!-, qui est, lui, par définition, à la verticale d'un observateur debout... ). Ce moment est celui où la trajectoire apparente du someil coupe le méridien du lieu (le grand cercle passant par les deux pôles et le point d'observation); à cet instant le soleil nous montre le sud exact.
Inversement, si le tracé du méridien est réalisé au sol, le soleil le coupe tous les jours (enfin, ceux où il se montre) au "midi solaire", ou plutôt, devrait-on dire, au moment de culmination.
Maintenant, faisons intervenir la révolution annuelle de la terre autour du soleil.
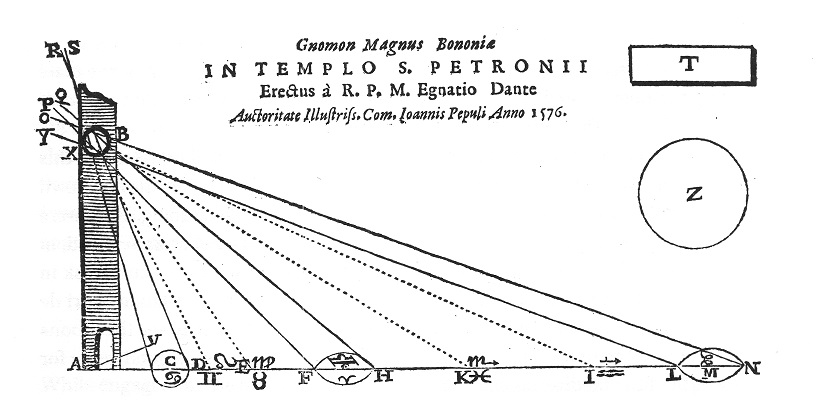
Tout le monde le remarque, le soleil est, à son point de culmination, plus bas en hiver (avec un minimum au solstice) et plus haut en été (avec un minimum au solstice). L'ellipse, trace solaire sur la méridienne, sera donc la plus allongée au solstice d'hiver, et la plus courte au solstice d'été. Ce qui apparaît fort bien sur ce dessin réalisé par le prédécesseur de Cassini, Egnazio Danti, qui, après avoir équipé de petits instruments la façade d'une église de Florence, avait construit en 1576 une première méridienne à San Petronio.
Revenons à celle de Cassini: ces deux ellipses "extrêmes" ont été gravées en taille réelle dans le marbre, aux extrémités de la ligne.
À l'extrémité sud de la ligne, il reste un peu de place pour un titre, et au mur, entre les chapelles, un panneau rappelle les principaux faits relatifs à la méridiennes: commanditaires, concepteur (Cassini), date de réalisation...
D'autres marques sont présentes (et importantes), nous les découvrirons plus loin.
Pourquoi la construire?
1. Des Nécessités Religieuses
La source de ces travaux est à rechercher bien
avant... au concile de Nicée (réuni en 325 à l'initiative de l'empereur Constantin), où l'on s'accorda après moult débats
sur la définition de la date de Pâques... en pleine inconscience de sa
difficulté et du casse-tête computationnel (oui, l'Église a conservé pour cela le mot latin comput -i.e. calcul, dont a été dérivé l'anglais computer, que nous n'avons pas été fichus de traduire par computeur, sous prétexte de ne pas adopter un mot anglais... pas de chance, il était latin!)| Pâques est le dimanche qui suit le quatorzième jour de la Lune qui atteint cet âge le 21 mars ou immédiatement après. |
C'est la définition qu' adopta le Concile de Nicée, ; la date du 21 mars avait été déconnectée de l'équinoxe de printemps, qui peut survenir entre le 19 et le 21. La définition était précise, mais n'était accompagnée d'aucun algorithme de calcul sûr!
Dès le départ, la question était viciée, puisqu'il s'agissait de combiner un calendrier solaire et un calendrier lunaire. Or, si tant est qu'il existe, le concepteur de l'Univers, "être omniscient et tout puissant" selon Newton, "Grand Horloger" de Voltaire, voire "Grand Architecte de l'Univers" cher à certains francs-maçons, a joué un vilain tour aux humains en général et aux astronomes en particulier: les périodes des deux mouvements n'ont pas un rapport rationnel ; et si c'est le hasard, on ne peut dire à ce propos qu'il ait bien fait les choses...
L'affaire s'était encore compliquée lors de la (nécessaire, évidemment!) réforme du calendrier de Grégoire XIII en 1582, en supprimant trois années bissextiles en 400 ans ( les années centenaires non divisibles par 400). Il fallut d'ailleurs attendre Gauss pour tenir une formule de calcul correcte!
Fût-ce à son corps défendant, l'Église avait donc besoin d'observations astronomiques précises, et en particulier relatives à la durée de l'année tropique (intervalle séparant deux passages du soleil à la même position dans son mouvement apparent autour de la terre), aux moments des solstices et équinoxes...
| " Le désordre où le calendrier Julien était
tombé parce qu'on avoit négligé quelques Minutes, avoit réveillé les
Astronomes du seizième siècle, ils voulurent avoir par observation les
Équinoxes & les Solstices que le Calendrier ne donnoit plus qu'à
dix jours près, & pour cet effet Egnazio Dante, Religieux Dominicain, Professeur d'Astronomie à Bologne, tira en 1575 dans
l'Église de Saint Pétrone une ligne qui marquait la route du Soleil
pendant l'année, & principalement son arrivée aux Solstices. On ne vcrut point mettre une Église à un usage profane en la faisant servir à des observations nécessaires pour la célébration des Fêtes." |
Et Danti, fort de son expérience de constructeur d'instruments à Florence, avait pour cela obtenu l'autorisation de l'instance qui "gérait" l'église, un conseil de 5 membres, les fabbricieri, émanation du puissant Sénat de Bologne, qui dirigeait la ville.
Mais San Petronio ne s'était pas laissé faire: où qu'il essayât d'installer son oculus, sa méridienne restait dans l'ombre toute une partie de l'année, la faute aux énormes piliers de la nef. comme le raconte Cassini dans ses mémoires (parues en France, d'où la: francisation des noms propres):
| "Ignace
Dante, dominicain, avait entrepris de tirer une grande ligne dans
l'église de Saint Pétrone pour les observations du soleil: mais s'étant
servi d'une ouverture faite dans la muraille méridionale de la nef
orientale de l'église,
les rayons du soleil à midi allaient rencontrer les colonnes, de sorte
que la ligne tracée sur le pavé avait été obligé de décliner de plus de
9 degrés; il n'y avait d'ailleurs aucune division qui pût servir à
connaître les hateurs du soleil" Anecdotes de la Vie de J.-D. Cassini, rapportées par lui même
|
C'était en 1576. Peu après l'arrivée de Cassini à Bologne (1650) pour y enseigner les mathématiques, en 1653, l'Église était à nouveau en chantier, et le mur percé était abattu. Les fabbricieri lui demandèrent de restaurer la méridienne de Danti, mais Cassini déclara qu'il valait mieux en construire une nouvelle qui remédierait aux défauts de l'ancienne; il réussit à les convaincre de financer ces travaux.
2. Les Motivations secrètes de Cassini
C'est
une tout autre ambition qu'avait Cassini: réformer de fond en comble
l'astronomie, et ainsi laisser un nom prestigieux dans l'histoire. La
présentation ci-dessous, au Musée scientifique de Bologne,résume bien
cette ambition...Portrait anonyme de Cassini, au dessus d'un automate planétaire. (Musée du Palazzo Poggi, Bologne) |
Il espérait trancher un débat qui agitait alors le monde savant, sur un point technique important: la bissection de l'excentricité. Et à travers celui-ci; l'affrontement de deux modèles: celui de Ptolémée, géocentrique, seul reconnu par l'Église,
et celui de Kepler, sous-tendu par le principe héliocentrique de
Copernic. Or l'ouvrage de ce dernier, le De Revolutionibus, avait été mis à l'index, quoiqu'on
pût à la rigueur l'utiliser comme hypothèse dans les calculs, mais surtout pas le diffuser publiquement, et encore moins sur le mode d'un pamphlet: c'est le style de ses Dialogues qui avait valu sa condamnation à Galilée en 1632, c'est à dire, pas si longtemps que cela avant... mieux valait donc avancer masqué!
|
|||||||
Ce
planétaire.(sans cartel permettant de le dater) est clairement
postérieur à l'époque du séjour de Cassini; en effet il obéit au modèle
héliocentrique. On peut le plus probablement l'estimer comme du XVIIIème siècle.
(Musée du Palazzo Poggi, Bologne) |
Comment la construire?
La première difficulté était de trouver le bon emplacement, et la seconde, de convaincre les fabbricieri d'ouvrir
leur bourse: il fallait pour cela, compte tenu de l'échec relatif de
Danti, une étude préalable minutieuse et un dossier administratif la
reflétant. En douterait on que les témoignages de Fontenelle et de
Cassini lui-même le confirmeraient:| "En
1653, on fit une augmentation au bâtiment de Saint Pétrone. Cela fit
naître à M. Cassini la pensée de tirer dans un autre endroit de
l'Église une ligne plus longue, plus utile, & plus exacte [...]
Comme il fallait qu'elle fût parfaitement droite, & que par la
nécessité de sa position elle devait passer entre deux Colonnes, on
jugea d'abord qu'elle n'y pouvoit passer, & qu'elle iroit périr
contre l'une ou l'autre. Les Magistrats qui avoient soin de la Fabrique
de Saint Pétrone doutoient s'ils consentiroient à une entreprise aussi incertaine. M. Cassini les convainquit par un Écrit imprimé qu'elle ne l'était point." |
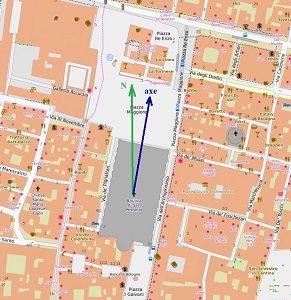
C'est que San Petronio avait le défaut de sa qualité: d'abord, l'avantage d'une orientation générale Nord-Sud, alors que la plupart des églises étaient traditionnellement orientées Est-Ouest.: l'urbanisme de la Piazza Maggiore l'avait emporté sur la tradition! Soit, une orientation plaçant le méridien géographique, et donc la ligne, dans le bon sens pour profiter de la plus grande longueur. Malheureusement, cette orientation était fort imprécise, comme n'importe quelle carte de la ville en apporte la preuve (aujourd'hui, le Nord est systématiquement place en haut de la carte), d'où la difficulté et le scepticisme engendré...
 |
|
| Le Problème... |
... et la Solution! |
| "Après avoir pris toutes les dimensions nécessaires, je m'aperçus qu'il était possible de tracer une longue méridienne qui ne rencontrât point les colonnes en passant entre leurs bases.
En conséquence, je cherchai et je trouvai dans la voûte un point élevé
de mille pouces du pied de Paris sur le pavé horizontal de l'église, par où l'on pourrait faire passer les rayons du soleil dont l'image devait être reçue sur la nouvelle méridienne. Cette hauteur, plus grande d'un tiers que celle du gnomon d'Ignace
Dante, demandait une longueur horizontale deux fois et demie plus grande,
c'est à dire de 2500 pouces, pour pouvoir servir à prendre toutes les
hauteurs méridiennes du soleil de l'un à l'autre tropique. Cette
longueur se trouva juste comprise entre le point perpendiculaire
au-dessous du gnomon et la muraille septentrionale de l'église, à
laquelle l'image du soleil devait arriver au solstice d'hiver. J'obtins donc une zone méridienne capable de recevoir l'image du soleil à midi tout le long de l'année. Je n'entrepris cet important ouvrage qu'après avoir pris les plus grandes précautions pour m'assurer de la possibilité de vaincre les obstacles qui semblaient se rencontrer tant en dedans qu'en dehors de l'église, dont l'architecture gothique présentait en différens lieux des inégalités et des difficultés d'exécution qui faisaient douter à plusieurs personnes de la réussite; aussi j'eus bien de la peine à persuader le sénateur qui présidait au bâtiment de Saint Pétrone, et à obtenir la permission de tenter mon entreprise [...]" Anecdotes de la Vie de J.-D. Cassini, rapportées par lui même
|
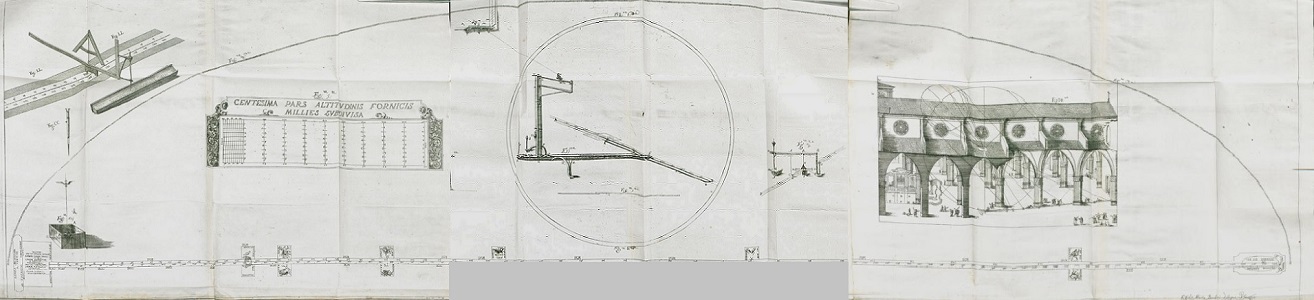
Image globale reconstituée par nos soins à partir de trois images de la numérisation originale ( e-rara, ETH Zürich )
Difficile en effet de trouver un scanner pouvant traiter en une seule passe cette feuille géante repliée à la fin de l'ouvrage!
Mais, direz-vous avec justesse, pour mettre en œuvre ce tracé, encore faut il connaître la direction de la ligne, car nous n'en possédons à ce stade qu'un point (à la verticale de l'œilleton. Cassini utilisa pour cela la méthode dite des cercles indiens, ou encore des ombres égales -ce qui sera plus parlant. Présentons la avec un bâton planté dans le sol (ou gnomon), qui matérialise la verticale de l'œilleton (le fil à pomb prédédent). Un jeu auquel n'importe qui peut jouer dans son jardin, la cour de son école (ou... la place de la Concorde avec son obélisque!) pour trouver le méridien du lieu.
Le midi solaire est le
moment où l'ombre du gnomon est la plus coutte... et dans la direction
de la méridienne: cela siuffirait en théorie,,mais la détermination
effectiveserait bien trop imprécise!
Au lieu de cela, traçons (avec une corde) un cercle centré sur le gnomon, et marquons y les points aux deux instants où l'extrémité de l'ombre est sur le cercle. Un même intervalle de temps les sépare du midi, l'un avant, l'autre après; et donc la ligne méridienne est la bissectrice de l'angle formé. Les deux ombres définissant un triangle isocèle, c'est aussi bien la médiatrice du segment joignant les deux points. Ce qui suffirait, puisque c'est également la hauteur du triangle: il suffirait de joindre au pied du gnomon. Pour plus de précision, il est prudent d'opérer avec plusieurs cercles, afin de tracer au mieux cette médiatrice commune... qui devrait être unique! |
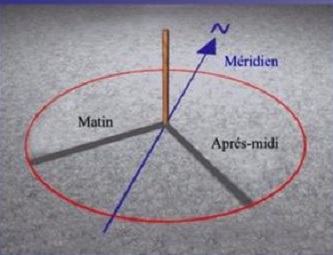 ( source de l'image ) |
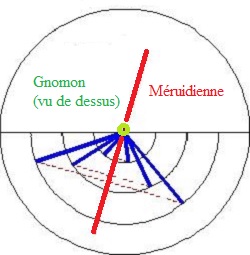 ( image modifiée d'après cette source ) |
C'est ce que fit Cassini, mais en opérant avec le centre de la tache elliptique... de quoi justifier encore davantage le recours à plusieurs cercles, car cela complique l'opération pratique!
| "Il [M. Cassini]avait pris ses mesures si justes , que la Méridienne alla raser les deux dangereuses Colonnes, qui avoeint pensé faire tout manquer." |
Cela se joue effectivement... au millimètre! Il a fallu recouper l'allée de marbre clair qui entoure la ligne, mais la ligne de métal elle-même ne fait que frôler les deux mastodontes. Ouf!
Il ne reste plus alors qu'à graduer la ligne, et en particulier poser les plaques zodiacales (marquant l'entrée du soleil dans chacune des 12 "zones" de 30° chacune, nommées d'après les diverses constellations fractionnant (virtuellement) l'équateur céleste, et tout particulièrement les plaques équinoxiales. C'est le moment de faire un peu de géométrie... et de trigonométrie! Et c'est ici qu'entre en jeu le mystérieux tracé que Cassini a superposé, dans son ouvrage, au dessin de la basilique. L'extraire pour le représenter "à nu" est la première opération à réaliser... mais il y faudra encore quelques éclaircissements. Et pour cela, reconstruire la figure pas à pas.
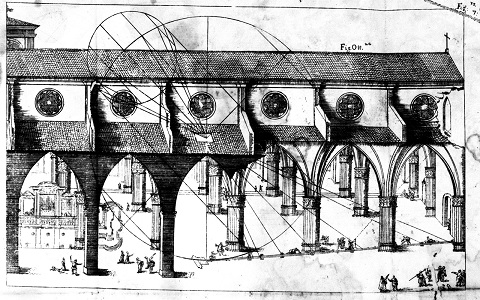 |
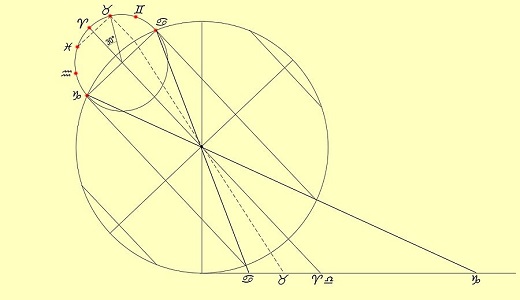 |
| figure de l'article Méridienne (gnomonique) de Wikipedia |
Commmençons par les marques equinoxiales, pour qui les cercles ne sont pas utiles, ou, pour le dire autrement, poursuivons le strip-tease de la figure. Il est souvent utile de procéder ainsi avec les figures qui, au premier abord, paraissent compliquées: repérer les traits qui nous sont utiles, éliminer ls autres... c'est à dire, ne pas avoir peur de prendre son crayon, ses stylos de couleur, et dessiner soi même à côté pour reconstruire pas à pas! Voici ce dont nous avons seulement besoin pour résoudre la preùière question: marquer les équi,noxes:
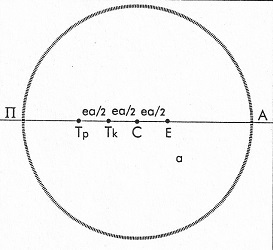
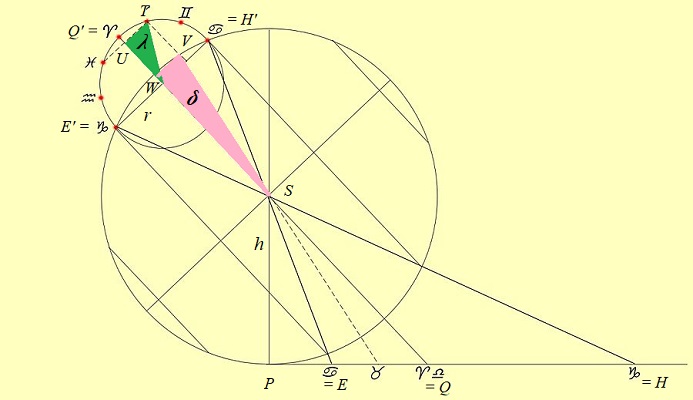
Premier (petit) interlude trigonométrique... si vous n'aimez pas ça, contentez vous des images, et oubliez les calculs!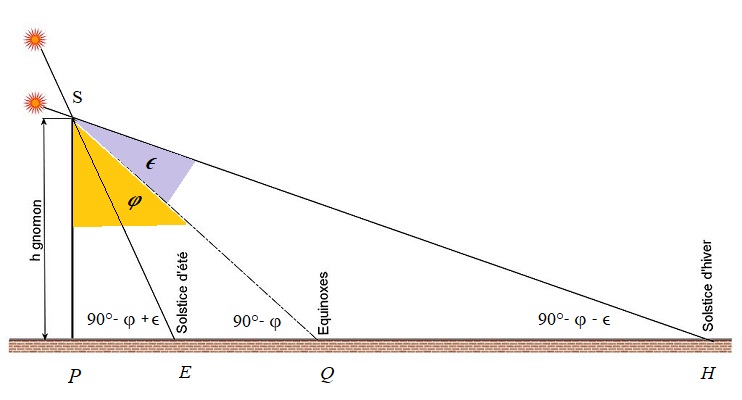 Aux équinoxes, le soleil est exceptionnellement dans le plan de l'équateur terrestre (ou aussi bien céleste): ce sont les moments où sa trajectoire le traverse. Ses rayons (considérés comme tous parallèles, car il est très loin) rencontrent le sommet du gnomon sous un angle égal à la latitude 4 (égalité d'angles alternes-internes), puisqu'ils sont alors parallèles au plan équatorial. La position du point Q des plaques éQuinoxiales sur la méridienne est donc telle que PQ = h.tan 4
P étant le pied du gnomon, et voilà pourquoi -entre autres- la latitude était utile! On peut aussi s'en passer, si les points E et H centres des ellipses solsticiales ont pu être soigneusement déterminées: PE = h.tan (4 - e) ; PH = h.tan (4 + e)
et l'on trouvera dans les tables les deux angles; en les ajoutant, cela permettra de trouver 24 et par suite de positionnsr Q. N.B. : le raisonnement pour trouver les angles rayons solaires/gnoùon est similaire; au solstice d'été, le soleil est à e au dessus du plan équatorial, et ses rayons font cette fois l'angle 4 - e avec le gnomon. |
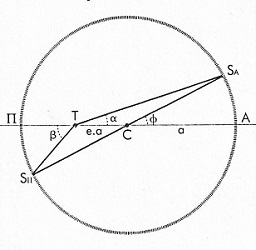
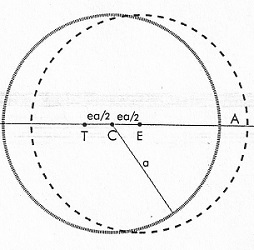
| Deuxième interlude trigonométrique (un peu plus long!)... si vous n'aimez pas ça, ... vous savez quoi faire! Ajoutons les deux cercles à la figure, et voyons en quoi ils peuvent nous aider. Le premier est centré en S, et il a pour rayon la hauteur du gnomon h . Le second a été construit en prenant pour diamètre H'E', intersections du cercle avec les rayons solsticiaux. Puisque l'angle SQH vaut e, on a la relation très simple r = h.sin e
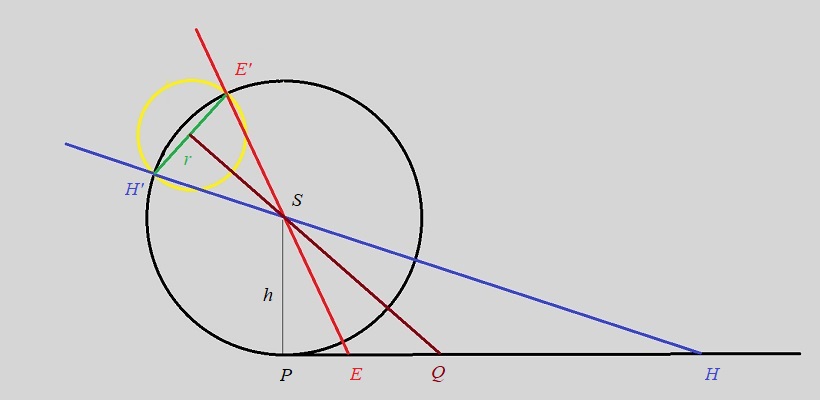 Autrement dit, le rapport r/h matérialise la quantité a priori assez abstraite sin e, où e est l'obliquité de l'écliptique.
|
Et voici la plaque portant le taureau (ainsi que le signe diamétralement opposé de la vierge)... et quelques autres!
| ici, on ne voit guère que les symboles conventionnels |
là, sagittaire et verseau, bien nets! |
lion et gémeaux, en regardant vers le sud (fond) | lion et gémeaux, en regardant vers le nord (entrée) |
Les deux dernières images font bien sentir le resserrement des signes vers le sud, conformément aux schémas donnés plus haut: la plaque du solstice du cancer est très proche de la plaque lion-gémeaux; alors que dans l'autre sens, la suivante (taureau/vierge) est nettement plus éloignée.
| "Ce
grand ouvrage étant fini, ou du moins assés avancé, M. Cassini invita
par un Écrit public tous les Mathématiciens à l'observation du Solstice
d'été de 1655. Il disoit dans un style poëtique, que la sécheresse des Mathématiques ne lui avoit pas fait perdre,
qu'il s'étoit établi dans un Temple un nouvel Oracle d'Apollon ou du
Soleil, que l'on pouvoit consulter avec confiance sur toutes les
difficultés d'Astronomie |
Allez, voilà encore un imprécateur prêt à rejoindre dans l'enfer des contempteurs de la Reine des Sciences, Stendhal et le Père Dupanloup...
Voici exactement ce que proclama Cassini dans son tract, avec un sens certain de la communication-spectacle, bien avant qu'on ait inventé des écoles pour ça... et il fera des émules, Foucault au Panthéon, entre autres!
| "Cet été, la première pierre sera posée dans l'église de San Petronio pour édifier la science céleste à partir du sol: le solstice sera observé, et la traversée de la méridienne par le Soleil sera définie; sur le pavé de l'église est une ligne méridienne, sur laquelle le Soleil, admis à travers la partie la plus haute de la voûte orientale, brillera toute l'année à midi précisément;
cette ligne, qui convient aux observations quotidiennes du Soleiln et
de la Lune, et des principales étoiles,et aux expériences physiques,
sera installée et exposée aux commentaires du public, les 21 et 22 juin, à 15h de l'horaire civil" J.-D. Cassini
|
Gageons que, si les réseaux sociaux avaient existés, il aurait demandé à un maximum de spectateurs de liker sa méridienne...
Voir fonctionner l'Instrument
 préparez votre visite en aggrandissant! |
Conseils aux visiteurs:
|
 |
 |
 |
Attention, tout va très vite: la traversée ci-dessus a pris moins de deux minutes! Belle occasion de prendre concrètement conscience de la vitesse de notre voyage annuel.
Observez aussi qu'à son "arrivée" sur scène, seule une demi-ellipse est visible, car le soleil tape partiellement sur le pilier.
Il est du reste possible de voir cela en temps réel, grâce à cette vidéo:
mais un conseil du Mathouriste: coupez le son pour éviter sa musique affligeante de nullité. Puisqu'il est question d'été, et pour rester en Italie avec de talentueux musiciens du pays, remplacez le par cet extraordinaire duo entre Roberta Gambarini (voc.) et Enrico Rava (tp) sur le célébrissimme thème de Bruno Martino , Estate. Et non seulement le son, mais aussi l'image!
Bien sûr, vous auriez pu choisir Chet Baker, ou encore Joaõ Gilberto... mais celui-ci recèle une jolie surprise!
Les Résultats de Cassini
Le temps était donc venu de soumette à l'instrument la grande controverse qui agitait le petit monde des astronomes.| "Un des principaux usages que je fis de mes observations à la nouvelle méridienne de
Saint Pétrone, fut de montrer par leur moyen que l'inégalité du
mouvement apparent du soleil ne dépend pas immédiatement de son
excentricité, qui est cause que son diamètre apparent paraît plus grand
dans le périgée que dans l'apogée. Mes observations firent voir que le diamètre apparent du soleil, qui diminue en s'éloignant du périgée du périgée, ne diminue pas à proportion comme le mouvement de cet astre danns l'écliptique. Kepler l'avait déjà avancé; mais les astronomes, entr'autres le père Riccioli, n'avaient pu se le persuader jusqu'alors. Le savant jésuite, convaincu par mes observations, auxquelles il assistait quelquefois, revint à l'opinion de Kepler, comme on le voit dans son Astronomie réformée. " Anecdotes de la Vie de J.-D. Cassini, rapportées par lui même
|  source: AMS Historica (univ. de Bologne) |
 source: AMS Historica (univ. de Bologne) |
Ainsi donc, l'Oracle d'Apollon trancha en faveur d'une excentricité
bissectée, en lui attribuant la valeur numérique 0,0167 (tout à fait
exacte; on l'estime ajourd'hui à 0,01671022), alors que la
théorie concurrente proposait 0,0334. En soi, ce n'était pas une preuve
irréfutable de l'héliocentrisme, car le mouvement elliptique et bien
réel de la Terre pouvait aussi bien s'interpréter comme un mouvement
elliptique du Soleil autour de la Terre... Il n'empêche, l'avantage
était à Kepler, l'homme qui avait réussi à déterminer la forme
géométrique correcte des orbites en s'étant appuyé sur le modèle de
Copernic. Comme il le dit dans le compte-rendu ci-contre (1666), il avait apporté "Une nouvelle lumière sur l'astronomie, grâce à un nouvel héliomètre"
Cassini tira également de ses mesures la valeur de l'inclinaison de l'écliptique : 23°29'05", corrigeant ainsi légèrement la dernière détermination de Tycho Brahé en 1590: 23°29'20". Lui-même refit la mesure en 1658 (23°28'55") et en 1658 (23°28'42"). On sait aujourd'hui qu'elle varie entre 22°02'33" et 24°30'16", selon un cycle de 41000 ans, selon lequel l'axe de la Terre décrit un cône, à la façon de celui d'une toupie lancée. Rien de sorcier sur la méthode, puisque la recherche des équinoxes avait mené à la détermination de (4 - e) ;et (4 + e). |
Laissons la conclusion philosophique à celui qui se chargea de son Éloge à l'Académie:
| "[...]
cet Instrument donne une précision telle qu'on n'eût oser l'espérer. Il
fut construit avec des attentions presque supersticieuses. Le Père
Riccioli, bon juge en ces matières, les a nommées plus angéliques
qu'humaines. Le détail en seroit infini... Dans
les Sciences Mathématiques, la Pratique est une Esclave, qui a la
Théorie pour Reine, mais ici cette Reine est absolument dépendante de
l'Esclave." |
Des tables compilant soigneusement les premières mesures effectuées avec cet héliomètre accompagnent la description de l'instrument,; outres les positions du soleil sont aussi étudiés sa parallaxe et ses réfractions.
Un peu d'Entretien
 source: AMS Historica (univ. de Bologne) |
Cassini lui-même revint en 1695, avec son fils, pour une révision
de l'instrument. Le tassement de l'église avait modifié la hauteur au
sol du trou dans le toit; c'est la comparaison avec les mesures d'une
autre méridienne qui avaient révélé le problème. Le même type de correction s'imposa à Eustachio Manfredi (1674-1739), qui restaura en 1698 la méridienne, quelque peu abandonnée.Des compte-rendus précis furent publiés pour chacune de ces opérations |
|
 source: AMS Historica (univ. de Bologne) |
||
 Zanotti, portait anonyme. Musée du Palazzo Poggi |
Mais c'est à une réfection bien plus approfondie que se livra son successeur Eustachio Zanotti (1709-1782), formé à Bologne et qui devint directeur de son observatoire en 1739. Il fit remplacer la tige de fer installée par Cassini, qui, inévitablement, avait subi les attaques de la rouille, par une ligne en laiton, en profitant pour remplacer les plaques zodiacales par celles que l'on peut admirer aujourd'hui. L'inauguration, le 4 octobre 1776 attira une foule de curieux, et déjà la méridienne était une curiosité réputée de la ville! Il dut intervenir à nouveau 3 ans plus tard, quand un tremblement de terre secoua la cité; heureusement, solide sur ses piliers, San Petronio résista à la secousse, et les dégâts, peu importants, furent vite réparés. |  |
|
| à droite, éphémérides publiés par Zanotti. L'image représente le Palazzo
Poggi, en ce temps siège de l'Académie des Sciences de Bologne et de
son observatoire astronomique, dont la tour est représentée. ci-dessous: sous les arcades, près de l'entrée du palais, une plaque vient rappeler qu'il fut maître des lieux au temps de l'observatoire. |
|||
 source: AMS Historica (univ. de Bologne) |
 |
||
Références
LE livre de J.L. Heilbron et des Commentaires
C'est évidemment l'ouvrage incontournable et inspirant sur le sujet.
Les deux denières références sont des mémoires d'étudiants à l'université de Singapour, dirigés par le Pr. Helmer Alasksen. Leur but est d'apporter quelques corrections et éclaircissements dans le texte et les figures. |
 |
 |
Historiques
- B. de FONTENELLE, Éloge de M. Cassini (Histoire de l'Académie Royale des Sciences)
- J.-D. CASSINI, La meridiana del tempio di S. Petronio : tirata, e preparata per le osservazioni astronomiche l'anno 1695
- Anna CASSINI, Gio. Domenico Cassini. Uno scienziato del Seicento (Comune di Perinaldo, 1994)
- Textes
en Ligne relatifs à
la Méridienne de Bologne (AMS Historica: Collections Historique de l'Université de Bologne)
Autres
- Article Méridienne (Gnomonique) de Wikipedia
- Article La Méridienne de San Petronio de 2005-Anno Cassiniano (pour les 350 ans de la Méridienne)
- Article La Méridiena di Cassini in San Petronio de l'Associazione Culturale Il Sestante (Astro,omie: Cassini)
Aller à la Page Autres Méridiennes : bientôt, sur cet écran!
Revenir à la Page Biographique
Revenir
à la
Page de l'Observatoire de Paris