 |
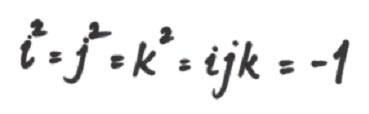 |
| brouillon réputé de la main de Hamilton (source: History of Ireland) |
 |
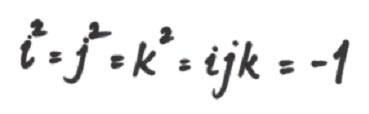 |
| brouillon réputé de la main de Hamilton (source: History of Ireland) |
En bref pour comprendre le contexte
Alors, on sait calculer, par les règles algébriques habituelles, le produit de deux nombres dits complexes(mais vous pouvez sauter et revenir après la promenade...) Toute la "magie" des nombres complexes, ou imaginaires, réside dans l'invention d'une racine carrée au nombre -1. Chez les nombres ordinaires, un carré est toujours positif, -1 ne peut donc en être un.
i² = -1-1 n'a pas de racine carrée? Qu'à cela ne tienne, on va lui en inventer une. Comme c'est le fruit de notre imagination, on va l'appeler i, ce sera un nombre imaginaire, vérifiant la relation (oui, la première qui est écrite sur la plaque) (a + ib) × (x + iy) = (ax - by) + i (ay +bx)
ce qui peut être vu comme produit du vecteur (a , b) par le vecteur (x , y) |
|
" (3) [...] S'il
m'est permis de parler de moi et de ma connexion au sujet, je peux le
faire en t'impliquant, en revenant à une époque pré-quaternionique, où
tu étais encore un enfant, mais un enfant qui avait appris de moi ce
qu'est un Vecteur, représenté par un Triplet, et je suis capable de mettre le doigt de ma mémoire sur l'année et le mois -Octobre 1843 [...]
Chaque matin de la première quinzaine du mois en question, vous
-toi et ton petit frère William Edwin, me posiez la question: «Eh bien,
Papa, as tu réussi à multiplier les triplets?» À quoi il me
fallait toujours répondre, en hochant tristement la tête: «Non , je ne sais que les additionner et les soustraire.»
Lettre à son fils Archibald, 05/08/1865)
|
"(4) [...]
Mais le 16 de ce même mois -qui tombait un lundi, jour de réunion du
conseil de la Royal Irish Academy que je devais présider, je marchais
le long du Canal Royal, aux côtés de ta mère, qui peut-être m'y avait
conduit; et, quoiqu'elle me parlât de temps à autre, un courant sous-terrain parcourait mes pensées, qui finit par me donner un résultat, dont il n'est pas excessif de dire que j'entrevis instantanément l'importance future. Ce fut comme si un circuit électrique se refermait, qu'une étincelle jaillissait, annonçant (je m'en rendis compte immédiatement) de nombreuses années de travail dans cette direction [...],
si seulement il m'était permis de vivre assez longtemps pour en
communiquer la découverte. Et je ne pus résister à l'impulsion -aussi
indigne d'un philosophe fût-elle- de graver avec mon couteau, sur une
pierre de Brougham Bridge, alors que nous y passions, la formule fondamentale liant les symboles i, j, k, à savoir
i² = j² = k² = ijk = -1
qui renferme la Solution du Problème,
mais qui, bien sûr, comme inscription, a depuis longtemps été effacée
par les années. Mais une trace plus durable en demeure dans les actes
du Conseil pour ce jour, qui ernregistrent le fait que je demandai et
obtins de faire à la première réunion pleinière de la session, une
communication sur les Quaternions; elle eut lieu, conformément à ce calendrier, le Lundi 13 Novembre suivant.Avec ce quaternion de paragraphes prend fin cette lettre; j'espère la faire suivre très rapidement d'une autre. Ton père affectueux,
William Rowan Hamilton |
 |
 |
|
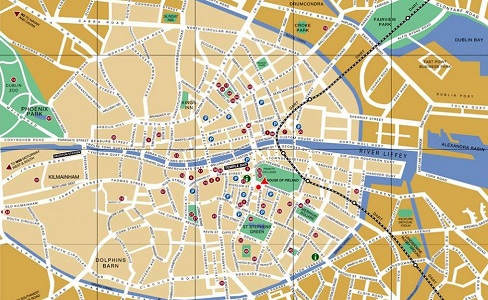
| plan actuel |
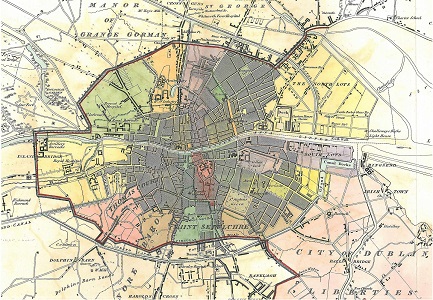
plan de 1837 |
Derrière son porche d'entrée un rien austère, c'est un jardin verdoyant que l'on découvre à Trinity College, bordé de bâtiments au style néo classique... ou so british! On y voit notamment la statue de George Salmon (1819-1904), mathématicien, spécialiste de Géométrie Algébrique, qui en fut aussi le doyen (provost est le titre officiel), et qui y côtoya Hamilton. Mais ne négligez pas non plus d'admirer l'œuvre d'Henry Moore, 'Reclining Connected Forms' (1969). |
|||
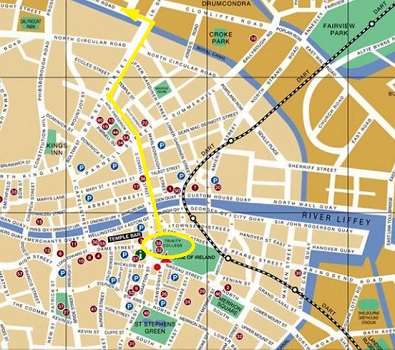 l'itinéraire que nous vous suggérons, en jaune! |
Mais il est temps d'entamer notre marche. Traversons la Liffey par O'Connell Bridge, poursuivons par la grande artère O'Connell Street, puis dans son alignement par Cavendish Row, jusqu'à rencontrer Dorset Street, que l'on prendra sur la droite sur la droite, jusqu'à ce qu'on franchisse le canal; il n'y aura plus alors qu'à tourner à gauche et longer le canal jusqu'à notre but. Quel intérêt à cet itinéraire plutôt qu'un autre? Une simple question d'ambiance... irlandaise, puisque nous passerons ainsi devant le pub The Auld Triangle, à l'angle de Gardiner Street. Or, The Auld Triangle, c'est aussi une chanson très populaire là-bas, et dont les lyrics insistent beaucoup sur le Royal Canal: ce n'est certes pas le sujet principal de la chanson -une sorte de blues d'un prisonnier, mais ce sont les deux vers de refrain que le public est invité à reprendre en chœur:
En outre, comme on le détaillera plus bas, l'Auld Triangle esyt le quartier où se situe la maison natale de notre héros! |
 Brassens vous le chante (source: INA) au premier plan, la main de Pierre Nicolas |
L'ami Georges vous le dira mieux que le Mathouriste ne saurait le faire: Il suffit de passer le pont
C'est tout de suite l'aventure Aventure, il y a bien pour Hamilton: il va falloir abandonner la commutativité de la multiplication, si naturelle, pour entrer dans un monde moins confortable et encore, pour beaucoup, à découvrir! |
Plus de détails sur la genèse de ces formules, par Hamilton in person
(Vous n'êtes pas obligés de lire; néanmoins, ne partez pas trop vite: après ce cadre, d'autres images et une deuxième promenade de Hamilton vous attendent!...) "Mon cher Graves,
C'est un très curieux enchaînement de spéculations mathématiques que jai vécu hier, et je ne peux quespérer qu'il vous intéressera. Vous savez que j'ai longtemps souhaité disposer d'une théorie des Triplets, analogue à celle des Couples que j'ai déjà publiée, et je crois que vous avez exprimé le même désir [...]. Je pense maintenant que j'ai découvert hier une théorie des quaternions qui englobe une telle théorie des Triplets. Voici comment se sont ordonnées mes pensées. Comme la racine carrée de -1 est, en un sens bien connu, une ligne perpendiculaire à celle de 1, il semblait naturel qu'une certaine autre quantité imaginaire déterminerait une ligne perpendiculaire à la précédente, [...]tout en étant aussi une racine carrée de -1, à ne cependant pas confondre avec la précédente. Appelant l'ancienne i , selon l'habitude des Allemands, et la nouvelle j, je cherchais quelles lois devaient régir le produit de (a + ib + jc) par (x + iy + jz) Il semblait naturel de supposer que ce soit (ax - by - cz) + i (ay + bx) + j (az +cx) + i j (bz + cy)
mais que faire de i j? Doit-il être de la forme (a + ib + jc)? Son carré semblerait valoir 1, puisque i² = j² = -1; et cela pourrait nous inciter à poser ij = 1 ou ij = -1;
mais aucune de ces suppositions ne nous permettrait d'avoir la somme des carrés des coefficients de 1 , i , j égale
au produit des sommes des carrés correspondants dans les
facteurs. Prenez le cas le plus simple du produit, lorsqu'il s'agit du
carré, on auraa² - b² - c² + 2 i ab + 2 j ac + 2 i j bc , et comme
la condition sur les modules est remplie, si l'on supprime le terme en i j [...](a² - b² - c²)² + (2ab)² + (2ac)² = (a² + b² + c²)² Voyez, je fus un instant tenté d'imaginer que ij = 0. Mais cela semblait singulier et malcommode, et je me rendis compte que la suppression du terme de trop [en français dans le texte] pouvait être effectuée avec une supposition qui me semblait moins dure, à savoir j i = - i j . Je posai donc ij = k , ji = -k , sans me soucier de savoir si k = 0 ou non. Reprenant alors le produit de deux triplets quelconques, (a + ib + jc) par (x + iy + jz), et cherchons si la loi des modules est satisfaite quand nous supprimons le terme en k. Est-ce que (a² + b² + c²)²(x² + y² + z²)² = (ax - by - cz)² + (ay + bx)² + (az + cx)² ?
Non, le premier membre excède le second de (bz - cx)². Mais c'est exactement le carré du coefficient de k dans le développement du produit (a + ib + jc).(x + iy + jz)
si l'on tient pour acquis ij = k , ji = - k
,comme proposé ci-dessus. Et là, je vis poindre l'idée qu'il nous faut
admettre, en un certain sens, une quatrième dimension de l'espace, afin
de pouvoir calculer sur les triplets; ou, en transférant ce paradoxe en
algèbre, admettre un troisième symbole imaginaire k, qu'il ne faut confondre ni avec i, ni avec j, mais qui est le produit du premier par le second, et qu'il faut donc introduire des quaternions a + ib + jc+ kd Je vis qu'on avait probablement ik = - j , parce que ik = i ij et i² = -1; et que de même on pouvait s'attendre à ce que kj = i jj = - i ; d'où j'ai pensé qu'il était probable que k i = j , jk = i car il semblait vraisemblable qu'à côté de ij = - ji , on ait aussi kj = - jk et ik = - ki. Et parce que lordre de multiplication de ces imaginaires n'est pas indifférent, nous ne pouvons pas en déduire que k² = ij ij = 1, en disant que i²j ²= (-1).(-1) = +1 . Il est préférable de voir que k² = i ji j = - ii jj = -1
[...] Mon système de relations était alors complet i² = j² = k² = -1;
et avec cela j'étais contraint à considérer que le produit de deux quadruplets est un quadruplet. [...]"ij = - ji = k , jk = - kj = i , ki = - ik = j , |
 source de l'image: site d'Anne van Weerden, consacré à Hamilton. | Un sculpteur sur sable, Daniel Doyle, a
réalisé (2012) une très belle restitution de la scène. Le Mathouriste, en découvrant cette image,
commença par douter: indéniablement émouvante (connaître simultanément
la jouissance scientifique de la découverte et la caresse d'un amour
sincère, what else?), n'était-elle pas trop belle, plus
belle que la vérité?
La biographie de R.P. Graves présente en effet un homme blessé de n'avoir pu épouser son amour de jeunesse. Il se serait alors marié pour respecter les convenances sociales de l'époque -quasiment indifférent sur le choix de celle qui partagerait sa vie: elles se valaient toutes si ce n'était pas celle pour qui il avait brûlé. Il s'était montré un bon père, certes, mais la relation avec une épouse qui, dans un premier temps, n'avait pas voulu résider à l'observatoire de Dunsink en l'y laissant seul apparaissait distante. Or, l'artiste a puisé son inspiration dans une nouvelle biographie, dont l'auteure, Anne van Weerden, défend, avec de nombreux témoignages de contemporains du savant, l'idée d'un mariage heureux dans une société victorienne qui ne faisait guère de cadeaux aux femmes. Voilà donc de quoi éclairer son choix. Alors, yes! Try a Little Tenderness, avec bien sûr Otis Reading, notre soul sister à tous: Aretha Franklin, ou le moelleux sax alto de David Sanborn. Hamilton romantique? En tout cas, il aimait la poésie, et n'hésitait pas à la comparer aux mathématiques: Mathematics is an aesthetic creation, akin to poetry, with its own
mysteries and moments of profound revelation. Et comme Omar Khayyam (voyez comme ses poèmes vont bien à ses équations de degré 3!) ou Lazare Carnot avant lui, il écrivait ses propres poèmes, et... il nous en laissé un à la gloire de Fourier! |
 |
 |
| le bâtiment de l'époque "hamiltonienne" |
dates de parution du feuilleton quaternionique ( in Elements of Quaternions ) |
Tout ce que vous avez toujours voulu savoir sur les produits de vecteurs (et qu'on vous cache le plus souvent) [ vous pouvez encore sauter cet encadré si vous n'avez jamais fréquenté ces bestioles...] 1. Les Quaternions au service des produits: Hamilton sépare son quaternion a + ib + jc+ kd en une partie réelle, a et une partie imaginaire (tout le reste, soit ib + jc+ kd, autrement dit tout ce qui comporte les 3 symboles "imaginaires" puisqu'ils sont de carré -1). Il est intéressant d'y voir apparaître le mot scalaire, par référence à l'échelle des nombres; quant à la partie imaginaire, elle a tout naturellement l'apparence d'un vecteur exprimé sur une base i, j, k . Il nous paraît intéressant de vous livrer son texte en V.O. parce qu'il n'est pas difficile et permet de saisir ce moment crucial pour ce qui va suivre.  Mais alors, grâce à sa théorie nouvelle des quaternions, il peut multiplier deux vecteurs... et contempler le résultat; ce n'est en général pas un vecteur, car il a aussi une partie scalaire. Il cherchait un produit de deux vecteurs? Voilà qu'il en obtient deux, en considérant la décomposition de son résultat. Vous allez assister en direct à la naissance du produit scalaire de deux vecteurs, et à celle de leur produit vectoriel: 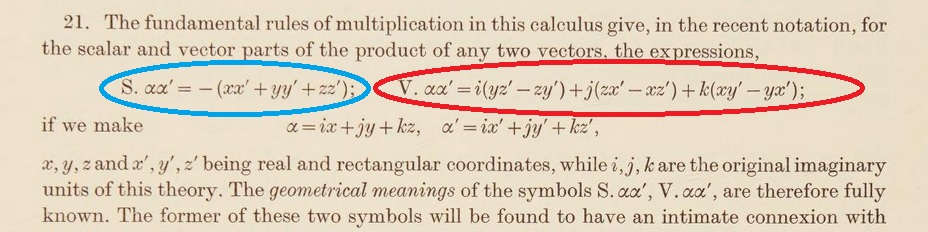 La conséquence la plus intéressante sera le développement par Josiah Willard Gibbs de l'Analyse Vectorielle: hélas pour Hamilton, elle éliminera totalement les quaternions de l'affaire, dans un but de simplification -Hamilton n'est pas facile à lire dans tous ses paragraphes, et avaler l'ensemble de sa théorie pouvait légitimement paraître indigeste à son époque,... et peut-être encore plus aujourd'hui!
2. Et le meilleur est à venir, et ce sera une contribution décisive pour la physique. Reprenons donc la lecture de Hamilton: .  Il vient d'introduire le pseudo-vecteur (opérateur différentiel, pour parler un langage mathématiquement châtié) qu'on appelera plus tard Nabla -il connaît le nom et l'écriture en "pointe vers le bas", mais la récuse dans un premier temps en préférant la diriger vers la gauche... Quoiqu'il en soit, il vient de donner naissance au calcul symbolique que développera ensuite Oliver Heaviside, et d'exprimer le laplacien grâce à son produit scalaire tout frais! Divergence et Rotationnel seront aussi clairement exprimés lorsqu'il poursuit  C'est Oliver Heaviside qui donnera l'écriture des
équations de Maxwell sous la forme limpide qu'elles ont aujourd'hui, qui emploie le Nabla, et
que le Mathouriste vous convie à lire sur le socle de sa statue à Edimbourg.
Le "malheureux" Maxwell, lui, avait écrit toutes les composantes, ce
qui faisait un joli paquet de formules, alors que l'écriture nouvelle
les réduit à 4, et surtout met en valeur leur "symétrie" et
l'esthétique de l'ensemble.
Note pour les étudiants qui auront à se servir du Nabla: peut-être avez vous ressenti -ce n'est pas rare!- ceci: "Nabla, c'est formidable, mais l'ennui, c'est que parfois, ça marche, et parfois, ça ne marche pas!" Ce n'est pas vrai, bien sûr; le problème est dans une utilisation fautive, avec une frontière entre le licite et l'illicite peu perceptible. À l'intention de ses étudiants, le Mathouriste a écrit, il y a pas mal de temps, un petit document, simple et pratique, (et, osera-t-on dire: infaillible?) que vous pourrez télécharger ici. Quaternions are Amazing and so is William Rowan Hamilton! (dans la série |
||||

| Eh oui! Avec Lara Croft, entre autres... Car les jeux vidéo, Tomb Raider
en tête, ont besoin de manipuler dans tous les sens (et le plus
rapidement possible, pour la crédibilité de l'action) les objets créés,
du vaisseau intergalactique à la charmante aventurière, en passant par
une quantité de méchants défiant le dénombrement.
Manipuler dans tous les sens, mathématiquement consiste à effetuer des rotations de l'espace. Or, dès leur naissance, les quaternions offraient un mode de représentation des rotations spatiales beaucoup plus compact que les autres outils mathématiques (par ex: angles d'Euler, matrices de transformation, pour les lecteurs qui connaissent). Et leur produit code exactement la composition (l'enchaînement, si vous préférez) de deux rotations! Pas d'hésitation: les formules de multiplication et division (et a fortiori, addition et soustraction) vont être bien moins encombrantes dans l'ordinateur. et plus rapide à effectuer: double gain! Le prix Nobel de physique 1969, l'américain Murray Gell-Mann l'a signalé dans sa conférence à Dunsink... un avis de poids, au cas où vous croiriez à une fantaisie de cette page. Vous trouverez plus de détails, notamment la comparaison du nombre d'opérations élémentaires requises entre nombres dans cette page Wikipédia, entre la méthode quaternionique et les autres.. Ce n'est pas une réelle nouveauté, cet outil avait déjà été utilisé en robotique... pour les mêmes raisons. Mais l'essor de l'informatique lui a donné importance nouvelle. Et cela ne concerne pas que le monde virtuel; un autre essor fulgurant, celui des drônes, a mobilisé les quaternions. À suivre... |

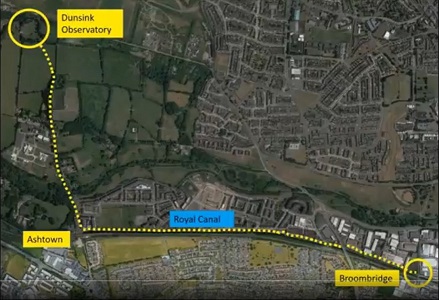
| On peut visualiser
le trajet ci-contre: l'observatoire est au nord du canal, et lorsque
les marcheurs l'ont rejoint (à travers champs!), ils arrivent au pont
par le côté opposé à celui suivi par le Mathouriste,
qui venait, lui, du centre ville. Si l'on se fie à ce que nous dit
Hamilton, il fait ce trajet, s'offre une petite pause gravure au pont,
et poursuit vers la Royal Acadeùy, dans le centre-ville: il y en a pour
8 km en tout. Cela ne semble pas lui faire peur, et d'ailleurs, c'est
très sain, pour le corps comme pour l'esprit: la marche favorise la
réflexion!
(a contrario, se faire déposer à la porte de son école en SUV est-il une bonne préparation à l'activité cérébrale?) |
| source de l'image: Capture d'écran de cette vidéo (marche 2020) |
 |
 |
| Fiacre O' Cairbre, Andrew Wiles et Anthony G. O’Farrell Marche 2003
|
Anthony G. O’Farrell, discours à Broombridge, Marche 2005
|

| Dodécaèdre à Borgo San Sepolcro, Italie (en hommage à Luca Paccioli et Piero della Francesca, natifs de la cité) |
Dodécaèdre à Urbino, Italie (en hommage aux mêmes, qui passèrent par là aussi) |
| A
contrario, si l'on voulait maintenir toutes les faces égales et
régulières, il faudrait "découper selon les arêtes": c'est ce que l'on
fait pour donner un patron 2D du solide (avec des onglets pour recoller
les faces et fabriquer un dodécaèdre en carton, les enfants
adorent...). Une raison simple en est l'impossibilité de couvrir les
360° autour d'un sommet avec 3 angles à 108° qui sont ceux du pentagone
régulier! Ainsi, le mathématicien -comme souvent- doit faire un choix: que conserver (ce sur quoi on ne peut pas transiger), qu'abandonner en se disant que c'est inutile pour le problème étudié. C'est tout l'art d'une négociation, qu'elle soit diplomatique, commerciale, ou... géométrique. Si on veut reconstruire le solide 3D, on opte pour le respect des faces, mais la découpe a fait perdre la propriété "3 arêtes arrivent à chaque sommet"; des onglets et de la colle y pourvoieront; pour le jeu icosien, seule la disposition relative des sommets et des arêtes compte, tant pis pour la longueur des arêtes et la surface des pentagones, qui n'intervient pas dans le jeu. | 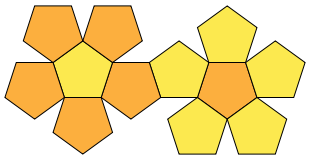 exemple de patron du dodécaèdre (Wikipedia) |
 |  |  |
 |
| Maison natale à Dublin. Photo de presse, 1938 (The Irish Independant) |
Détail de la porte d'entrée Archives de la RTÉ (Radio Télévision de l'Eire) | Article relatant la démolition (1964) |
La Plaque (aujourd'hui à Dunsink Observatory) |
| Toutes ces images proviennent de cette page du très complet, très documenté site d'Anne van Weerden, A Victorian Marriage, William Rowan Hamilton On vous le recommande vivement! |
|||
|
Tony
O’Farrell, Leo Creedon, Anne van Weerden, Donna Cooney
(représentante
de la municipalité), |