Lost in Translation...

... Jamais avec Toit! (Surfaces Architecturales)

N'hésitez pas à agrandir, pour mieux voir, les deux images ci-dessous... mais patientez un peu pour savoir de quoi il s'agit, et où cela se trouve!


" La voûte le l'église consiste en une harmonieuse structure ondulée, en voûte de béton armé à double courbure, reposant sur dix fins piliers en forme d'échasses [...]." dit le livret de présentation du premier édifice

Qu'y a-t-il de commun entre ces deux toitures?

Ni la matière: béton pour l'une, ossature métallique pour l'autre,
ni l'état de conservation... particulièrement inquiétant pour la sseconde.

Non, ce qui les unit dans une même espèce, c'est la géométrie! Toutes deux illustrent un principe commun: faire glisser, parallèlement à elle-même, une première courbe en la fixant le long d'une seconde. Si vous croyez que c'est compliqué, c'est que vous n'avez jamais bien regardé dans votre penderie: les courbes qui glissent parallèlement à elles-mêmes, ce sont les cintres, et la courbe "porteuse", la tringle de la penderie. Au passage, ne résistons pas à cette observation: même dans une penderie, rien n'oblige les contres à être dans des plans perpendiculaires à la tringle... la preuve ci-contre!
	(penderie 1)	(penderie 2)

Ultime remarque avant de quitter notre penderie: avec de bon vieux (pour ne pas dire antediluviens) cintres dont la pièce de bois a la forme d'un arc de cercle, la surface décrite lorsque le crochet balaye la tringle support est une portion de cylindre, de révolution lorsque la tringle est horizontale (penderie 1), elliptique lorsqu'elle est inclinée (penderie 2).

Enfin, peut-être avez vous été effrayé par l'expression savante double courbure?

Bon, soyez raisonnable: êtes vous impressionné, si ce n'est favorablement, par l'image ci-contre (qui provient de notre page consacrée au mathématicien-vigneron Charles Méray)? Vous venez, en bon Monsieur -ou Madame!- Jourdain, de découvrir une surface à double courbure: on y voit en tout point deux courbes orthogonales de rayons différents, les cercles horizontaux (matérialisés par les cerclages du tonneau) et les planches "verticales", formant la précieuse cuve et cintrées en arcs de cercles -au moins en première approximation), à moins que ce ne soit d'ellipse... peu importe, d'ailleurs, car en adoptant le modèle d'une conique, cela permet, jolie découverte de Kepler, d'en donner une formule pour le volume, ce qui, convenez en, est bien le point essentiel.

Le Mathouriste vous invite maintenant à découvritr quelques toitures qui obéissent à ce même principe. Mais histoire, d'abord de bien vous familiariser avec cette notion, ensuite de respecter une gradation en complexité mathématique, et enfin... de maintenir le suspense avant de vous dévoiler qui sont les deux monuments introductifs, commençons par les cas les plus évidents, mais touristiquement plus exaltants qu'un voyage dans votre dressing.

Exemples élémentaires

Les Cylindres

Pour inviter au rêve et au dépaysement, la visite du célébrissime GOUM de Moscou -ce grand magasin d'Etat du régime communiste devenu le plus insolent temple du luxe, de la comsommation effrénée et du capitalisme mondialisé s'impose: son toit est un demi-cylindre dont la charpente métallique est formée de droites horizontales, et de cercles verticaux, qui se translatent le long de la génératrice sommitale: c'est l'expression la plus simple et la plus naturelle d'une surface de translation.

Mais on peut aussi la voir comme un ensemble de droites, qui se translatent le long d'un arc de cercle! C'est en fait une propriété générale des surfaces de translation qui le sont toujours de deux façons, à partir des deux familles de courbes (ici, cercles et droites) qui les définissent.

Le bâtiment et sa verrière furent édifiés entre 1890 et 1893. Le demi-cylindre de fer et de verre a un diamètre de 14m.

La Place Rouge et le Goum: illuminations nocturnes à Moscou (Russie)


la nuit tombe sur la verrière cylindrique du Goum, rehaussée par les illuminations du Nouvel An (Moscou, Russie)

Monument à Shukhov,
place Turgeniev, Moscou

Mais au fait, à qui doit-on ce chef d'œuvre de simplicité et de luminosité? À l' "Eiffel Russe", Vladimir Shukhov (1853-1939), dont nous vous avons fait découvrir ici la géniale adaptation en architecture métallique de l'hyperboïde , et là le monument moscovite à sa mémoire, dont l'image ci-contre ne vous dévoile que la statue sommitale... or la base mérite qu'on s'y attarde!

Comme on le verra plus loin, ce choix n'a rien de fortuit. Il existe, de par le monde, un certain nombre de galeries couvertes dont le toit est conçu de manière similaire; nous vous proposons un exemple napolitain. C'est la galerie Umberto I, construite par l'architecte Emanuele Rocco sur le modèle de la galerie Victor-Emmanuel II à Milan, à ceci près que dans cette dernière, le cylindre de verre est "cassé" par un prisme sommital qui nuit à la pureté de l'œuvre. Elle est l'exacte contemporaine (1887-1891) du Goum, tandis que sa grande sœur milanaise avait été édifiée 25 ans auparavant.

Les autres cylindres jouissent évidemment de la même propriété: ce sont des surfaces de translation., mais "à simple courbure" (les lignes orthogonales aux cercles sont des droites, leur courbure est nulle)

Les Paraboloïdes

Le paraboloïde hyperbolique est une surface de translation: l'équation

z = x² - y²

montre clairement que les sections x = a sont des paraboles x = a, z = a² - y² clairement translatées de la parabole x = 0, z = - y² qu'enfourche allègrement le cowboy; elles s'appuient sur la ligne y = 0, z = x² (le dos du cheval). Si vous n'êtes pas rompu aux équations... le plus simple n'est-il pas de regarder une vraie selle de cowboy, pour vous persuader de la justesse de la comparaison?

Selle "Grimsley" (1847)
The Cow-Boy Museum and Hall of Fame, Fort Worth (Texas)

Cette fois, on saisit bien qu'il y a double courbure, mais pas de la même manière que dans le cas du tonneau: on parle parfois de courbures oppsées; le tonneau est convexe, pas la selle. Le paraboloïde elliprique est, lui aussi, une surface de translation: c'est tout aussi immédiat à voit sur l'équation (changeons un "" en "+", et l'affaire sera faite!). Mais cela ne semble pas très évident à découvrir sur une toiture qui le soulignerait... la chasse est ouverte!

On peut démontrer que, parmi les quadriques propres, les paraboloïdes sont les seules surfaces de translation. Ce qui signifie que l'aventure va se poursuivre avec des équations de degré plus élevé...

Le Couvent des Dominicains , à Lille

C'est lui, notre premier bâtiment! Inauguré en 1957, il est classé à l’inventaire supplémentaire des monuments historiques, premier bâtiment religieux labélisé “Patrimoine du XX^ème siècle”.


Lille, le Couvent des Dominicains, avenue Salomon

D'emblée, on remarque la répétition des arcs de cercle, dans deux directions de plans perpendiculaires. Ils rythment toute larchitecture de l'édifice, et vont introduire naturellement des surfaces de translations cerclées.
Ces bâtiments ont été conçus par l'architecte Pierre Pinsard (1906-1988), assisté de l'anglais Neil Hutchinson, puis du suisse Hugo Vollmar. En effet, la construction s'est étalée sur plus de 10 ans, des premières esquisses (1953) à l'achèvement (1964). La collaboration avec le prieur du couvent, le frère Bous, est totale.

"P. Pinsard était un homme merveilleux et notre collaboration a été sans nuage. Très vite, une amitié s'est nouée entre nous. Il avait une personnalité très riche. C'était un caractère! Dans les réunions de chantier, il ne tolérait pas l'à-peu-près. Ses plans avaient d'ailleurs une qualité et une précision qui étonnaient les entreprises."

Frère Michel-Robert Bous, interview, juin 2000

"Pinsard s’est toujours associé avec d’autres architectes, comme il l’était, par exemple, avant mon arrivée, avec Neil Hutchison. Non diplômé, sans formation technique, maîtrisant peu la méthode du dessin à l’encre des plans d’exécution précis, côtés, renseignés selon les règles en cours et contractuels, il avait besoin de s’entourer. Son cursus était davantage artistique que technique. Sûrement, gardait-il à cet égard une sorte de complexe, des hésitations et une grande prudence. [...]. En revanche, c’était un remarquable dessinateur qui avait travaillé avec Raoul Dufy. Il adorait dessiner, faire des croquis, exécuter des perspectives au crayon.

Homme instinctif, très cultivé, plein de sensibilité et de charme, passionné de musique, il aimait séduire ses interlocuteurs. C’est comme cela qu’il est rentré en contact avec des écrivains comme Blaise Cendrars.[...] S’il se disait athée, en fait, Pierre Pinsard était profondément religieux, mais il doutait. "

Hugo Vollmar, interview, juin 2000

Ce deuxième témoignage est particulièrement intéressant, puisqu'il nous assure que c'est par l'intuition et le sens esthétique que Pinsard va parvenir à des surfaces mathématiquement remarquables, et non par volonté d'illustrer des équations déjà connues de lui. Les religieux affirment souvent que les voies du Seigneur sont multiples... celles de la beauté mathématique le sont assurément, et rien que pour les surfaces, le Mathouriste espère que le lecteur s'en convaincra en explorant ses autres pages.

Le Cloître, les passages

Patientons encore un peu avant d'étudier l'église: le cas des couloirs est géométriquement plus simple. Le porche franchi, le visiteur accède à une première cour bordée de couloirs couverts; elle délimite un espace intermédiaire entre la rue (le monde extérieur) et les bâtiments conventuels, réservés aux Dominicains, plus en retrait. Cette disposition permet en particulierd'offrir l'accès de léglise à tous.


Couvent des Dominicains: première cour

Pour ce qui nous intéresse, il convient de lever les yeux vers la couverture: elle répète un motif qui se projette au sol selon un carré. Sur les bords du couloir, des arcs de cercle servent d'appui aux cercles de plus grand rayon qui couvrent le passage, faits de béton au niveau des piliers, de lignes de briques entre. Un esprit chagrin dirait qu'avec des briques, on ne peut construire qu'une ligne polygonale inscrite... mais le choix d'un rayon plus grand et une réalisation très soignée donnent vraiment l'impression d'un cercle! Et ce n'est pas Archimède, qui déjà évaluait avec précision pi de cette manière, qui oserait nous contredire! Les arcs de cercles en briques sont tous de même taille, nous sommes donc en présence d'une surface de translation.
Et si le sens de placement des briques favorise la lecture en "cercles de grand rayon s'appuyant sur des cercles de petit rayon", géométriquement, la surface pourrait aussi bien être vue comme ensemble de cercles de petit rayon parallèles, s'appuyant sur deux grands arcs bétonnés.

"De bons esprits se sont demandés s'il existe une sorte de hiérarchie des matériaux. Il peut sembler en effet que le matériau naturel (pierre, bois) a une certaine supériorité sur le matériau obtenu: métal, béton, glace, plastique, etc... En fait, je crois que c'est la façon de traiter la matière et de lui insuffler l'esprit qui compte. Je ne crois pas à un style architectural religieux. Il y a l'architecture dun temps donné et son expression religieuse.[...]

On entend souvent: ça fait usine! Et alors, pourquoi pas: il y a de très belles usines. Les matériaux passés au crible de notre intelligence et de notre cœur sont notre langage et doivent nous permettre de nous exprimer en glorifiant le Créateur de toutes choses."

Pierre Pinsard, conférence, Gand 1960

Le même système de surfaces de translations à génératrices circulaires se retrouve dans les couloirs du grand cloître. À l'origine, ils étaient ouverts sur la cour: seuls apparaissaient les arches et piliers en béton brut. Les verrières plus récentes maintiennent certes la lumière, mais les menuiseries en plastique égratignent le programme en faisant peu de cas (sous couvert d'amélioration thermique?) de la noblesse des matériaux que l'on vient d'évoquer. Où il est prouvé que la brutalité n'est pas nécessairement du côté du brutalisme...


Couvent des Dominicains: grande galerie du cloître

Origines mathématiquement... Bohémiennes?

Cette surface est mathématiquement répertoriée sous le nom de dôme bohémien. Le nom provient de la région où exerçait celui qui l'étudia de façon approfondie (1884): Antonin Sucharda (1854-1907), professeur d'université à Brno, en... Bohême (aujourd'hui, en République Tchèque). Certains auteurs réservent l'appellation au cas où les deux cercles ont même rayon; d'un autre côté, Sucharda a généralisé à des surfaces de translation engendrées par deux coniques, ce qui légitime le nom dans notre cas où les rayons diffèrent.		Le dôme bohémien, clooection de modèles de l'Institut Henri Poincaré (Paris)
	Mais attention! Pour voir ce modèle en plâtre comme le toit des couloirs précédents, il faut lui faire subir une rotation de 90°, comme illustré à gauche. On retrouve bien alors la double génération cerclée dans la même disposition. C'est très facile sur l'image... Cela aurait été impossible physiquement, du moins sans un support en fil de fer! (La surface aurait reposé sur un point unique, l'étagère constituant le plan tangent en ce point)
	Le dôme bohémien une surface du quatrième degré, comme le tore; mais dans le cas du tore, un cercle est en rotation en s'appuyant sur un autre cercle, au lieu d'être en translation dans le dôme bohêmien. Si vous avez envie de voir cette équation plus en détail, rendez-vous sur la page dédiée du site mathcurve.com de Robert Ferréol. Elle présente une auto-intersection, comme on le constate sur le modèle. N'oublions pas que le toit n'est qu'une portion, tout à fait lisse, de cette surface.

L'appellation voûte bohémienne paraît avoir été, antérieurement à Sucharda, en usage dans les descriptions architecturales; elle est parfois assez vague, et peut alors se voir appliquée à différentes formes géométriques (dont sphère, paraboloïde...), en fait à une voûte à deux courbures posée sur un carré ou un rectangle.

Ci-contre, à titre d'exemple, un Manuel sur l'Art de la Construction (1820) manifestement à l'usage des ingénieurs, dit à peu près ceci, à l'issue du double exercice de réécriture dans une police civilisée, puis de traduction (la première étape ayant été jugée indispensable...)

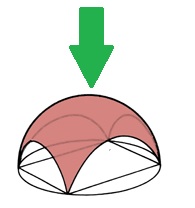"On obtient une Voûte Bohémienne en inscrivant un rectangle dans la base d'une voûte sphérique ou elliptique, puis en élevant sur les côtés de ce rectangle quatre plans verticaux qui coupent cette première surface [...] Mais la forme des dômes bohêmiens est sujette à de nombreuses variantes."

Clairement, il s'agit d'une extrapolation d'un modèle classique, le dôme hémisphérique, ou dôme suspendu, reposant sur quatre pilers disposés en carré. L'idée est d'aplatir la calotte sphérique; la page Wikipedia allemande en donne une définition maladroite, un peu naïve, mais on voit l'idée...

" Le dôme bohémien est une forme de la voûte apparentée au dôme suspendu. La voûte lisse en est étirée sur un plan d'étage principalement carré. Les arches délimitant le champ voûté, visibles sur les parois latérales, ne sont pas semi-circulaires dans la calotte bohémienne, mais forment des arcs très aplatis, ce qui rend cette voûte beaucoup plus plate que le dôme suspendu."

Quant aux pages anglaises et françaises, elles n'en parlent tout simplement pas! Cette lacune a un intérêt: elle souligne clairement la zone géographique où le principe s'est développé. Divers ouvrages techniques, de la première moitié su XIX^_ème siècle, emploient l'expression et donnent des définitions tout aussi proches, et tout aussi peu fixées géométriquement; dès lors, la dénomination a dû s'imposer naturellement à Sucharda.

Reste, direz vous, à trouver l'objet... en Bohême! Patience, nous y reviendrons plus loin. Et notons, avant de revenir à notre couvent, dont la visite est loin d'être terminée, que l'expression n'échappe pas à l'érudition encyclopédique d'Umberto Eco

" Au bout de quelques petites minutes, Aglié entrait. «Veuillez m'excuser, mes chers amis. Je sors d'une discussion désagréable, et c'est peu dire. [...] Mais suivez-moi, je vous prie, dans mon petit cabinet de travail, où l'atmosphère pour converser sera plus confortable.»

Il souleva la portière de cuir, et nous fit passer dans l'autre pièce.[...]Ce jeu de lumières différentes, aussi innaturelles les unes que les autres, d'une certaine façon ravivait cependant, au lieu de l'éteindre, la polychromie du plafond.

C'était un plafond en voûte, que la fiction décorative voulait soutenu aux quatre côtés par des colonnettes rouge brique avec de petits chapiteaux dorés, mais le trompe-l'œil des images qui lenvahissaient, réparties en sept zones, lui donnait des allures de voûte bohémienne, et toute la salle prenait le ton d'une chapelle mortuaire, impalpablement peccamineuse, mélancoliquement sensuelle."

Umberto Eco, Le pendule de Foucault

Dès lors, pourquoi ne pas poursuivre cette visite virtuelle avec les Airs Bohémiens de Pablo de Sarasate... à moins que vous ne préfériez le Saint Thomas de Sonny Rollins, puisque c'est le nom du couvent!

Mais revenons au cloître; il faut en remarquer tout particulièrement un angle. Parce qu'il met en valeur la statue ancienne en bois dans la niche (noter l'arc supérieur de la niche, qui reprend l'unique élément de courbe, l'arc de cercle, sur lequel l'architecte construit tout son édifice: admirable sobriété de Pinsard!) mais aussi parce qu'il nous présente une...intersection.


Couvent des Dominicains: première cour

Il y a de quoi surpendre, de prime abord: les deux couloirs ont même largeur, il suffirait donc, mathématiquement, de prendre pour toit de l'angle... un unique dôme de Bohême! Lisible en cercles parallèles de même taille dans les deux directions, il constituerait le raccord parfait. Alors, pourquoi voyons nous autre chose? Probablement parce que, si la solution est géométriquement parfaite, elle ne l'est pas du point de vue du matériau: les lignes de brique privélégiraient une direction au dépens de l'autre. La solution esthétique a donc été de substituer l'intersection de deux voûtes cylindriques, qui, puisque les cylindres sont de même taille, est formée de deux ellipses, bien visibles sur les images. (Ce cas est présenté plus en détail, sur d'autres édifices, dans notre page sur les intersections de cylindres)

Mais, comme nous l'avons signalé d'emblée, les cylindres sont des surfaces de translation: le programme architectural garde donc une parfaite cohérence géométrique! Il y a d'ailleurs d'autres toits cylindriques dans le bâtiment, en voici deux exemples qui en diront plus long que tous les discours:


Le réfeectoire	La salle commune

L'église

Pénétrer dans l'église, c'est à coup sûr être saisi par l'élégance de la composition architecturale: sobriété des murs et de leurs vitraux, finesse des piliers tronc-coniques (pointe vers le bas, comme dans le palais de Minos en Crète -à voir dans cette page), entièrement décollés des murs. Ce n'est que peu à peu que le regard s'élève vers ce qui était censé être notre intérêt géométrique premier: le voile de béton qui en forme le toit. Et pourquoi ne pas s'instruire de l'intention artistique, avant de passer à l'aspect géométrique?

"La symbolique de l'église est celle d'une tente de bédouin faite de perches verticales soutenant des toiles, au plafond et sur les côtées. Il s'agit là d'une double réminiscence: d'une part celle de la tente de la rencontre (avec Yahvé) que Moïse construisit durant l'exode des Hébreux fuyant la maison d'esclavage, l'Egypte. D'autre part, c'est surtout une illustration de l'évangile selon Saint Jean qui dit que le Christ [...] a «planté sa tente parmi nous» par son incarnation, La double courbure du velum de béton de la voûte soutenue par dix colonnes, signifie le mouvement du vent de l'esprit de Dieu faisant ondoyerla toile du plafond."

Livret de présentation du couvent, non daté

Les marques de coffrage, bien visibles, ne laissent aucun doute: ce plafond est construit comme une surface de translation: d'un mur latéral à l'autre, les arcs de cercle définis par les fenêtres hautes, reprenant le leit-motiv repéré dans toutes les autres parties du couvent, se tranlatent, égaus à eux-mêmes, perpenduiculairement à l'axe de la nef. Reste une question: sur quelles courbes ondoyantes s'appuient-ils?


Admirer à la fois l'élégance du toit et celle des claustras de vitraux: simplicité et pureté.

Si la première idée qui vient est celle d'une sinusoïde très aplatie, la technique de construction, qui utilise des formes en bois pour les coffrages, suggère, au nom de la simplicité, un enchaînement de (trois) grands arcs de cercle, avec inversion de la concavité aux raccords; celle-ci est bien marquée sur le dessin original. Ce qui fait de la portion du toit entre deux piliers le recollement de trois dômes bohémiens! Les images connues du chantier en cours peuvent accréditer cette idée.


Source des images: Historique du Couvent des Dominicains (sur le site web du couvent)		Dessin de l'architecte (source: site de P. Pinsard)

En effet, que l'autodidacte Pinsard ait eu une connaissance, même vague, du modèle de la sinusoïde est aussi peu probable que la construction d'une forme en bois de ce type: elle n'aurait pu se faire qu'à l'aide d'un relevé de coordonnées, avec un dessin à main levée entre les points marqués. C'est, à l'évidence, très malcommode, alors que menuisiers et charpentiers maiîtrisent le cintrage à rayon fixe (ou, tout au moins, une bonne approximation...). Des cours d'architecture n'auraient sans doute pas changé cet état de choses, tant ceux-ci, en France, sont (à de rares exceptions près) peu orientés vers les matières scientifiques et techniques: si un Iannis Xenakis (lui aussi spécialiste des voiles minces) a pu faire exception, c'est parce qu'il avait été formé... à l'Université Polytechnique d'Athènes.

Nous conclurons donc, jusqu'à plus ample informé, que la seule courbe utilisée dans ce bâtiment est l'arc de cercle, tant pour satisfaire une unité de conception attestée par toutes les voûtes et fenêtres, que pour avoir une technique de construction efficace et rapide.

Où l'on retrouve Shukhov...

Le second bâtiment de notre introduction, carcasse de feraille en ruine sur l'image, est ce qui reste d'une usine métallurgique édifiée en 1897-98 à Vyksa (à 150km de Nizhny-Novgorod). par l'architecte du Goum, Vladimir Shukhov. Il est considéré comme le tout premier exemple d'une structure métallique à double courbure en réseau de poutrelles. Auparavant, l'ingénieur-architecte avait testé l'idée du double réseau "en diagonales" sur des toits cylindriques; son but était d'obtenir plus de solidité avec moins de matière, avantage à exploiter tant pour économiser le métal que pour agrandir l'empattement de la halle.

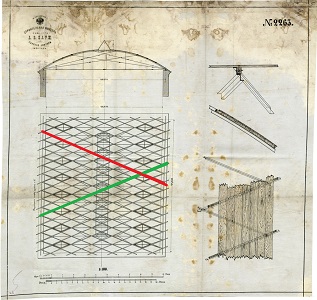
"Shukhov avait entamé la construction de charpentes métalliques voûtées en 1890, afin de recouvrir deux stations de pompage à Grozny. La section droite des toits était un arc de cercle, d'empattement approximatif 9m. En vue du dessus, la structure offrait l'aspect d'un réseau "en as de carreaux", formé par deux familles, symétriques par rapport à la section droite, de poutrelles parallèles. Dans l'espace, celles-ci formaient donc des ellipses, rivetées à leurs points d'intersection.[...] Il breveta ce système en 1895 pour des surfaces à simple courbure et l'appliqua en différents endroits, notamment à la foire-exposition de Nizhny-Novgorod." M. Beckh, R. Barthel, The First Doubly Curved Gridshell Structure - Shukhov's Building for the Plate Rolling Workshop in Vyksa. (Congrès, 2009)
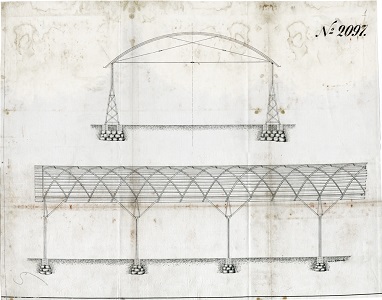	plans originaux de Shukhov pour une voûte à simple courbure (source) les sections par les plans rouge et vert sont elliptiques, puisque la section droite (représentée au dessus) est circulaire.

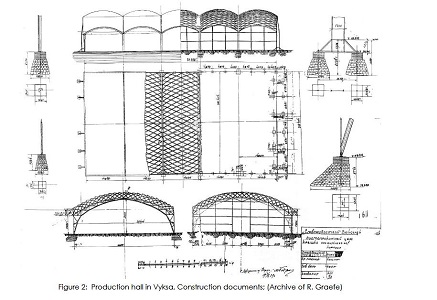
Il ne lui restait plus qu'à avoir l'idée de recourber les génératrices droites du cylindre pour parvenir à une charpente à double courbure: c'est ce qu'il fait pour l'usine de Vyksa. Et voilà le résultat!


plan et gravure de l'usine de Vyksa, reproduits dans l'article de Beckh & Barthel à partir d'un livre de R. Graefe

La maquettte ci-dessous, réalisée à l'occasion d'une exposition à Moscou (2019-2020), fait bien apparaître à la fois le réseau "diagonal" et le fait qu'il s'agit de surfaces de translation... MAIS!

... mais une question se pose: si l'arc sur le petit côté du rectangle a nettement une apparence circulaire, celui qui est défini sur le grand côté fait davantage hésiter; au premier coup d'œil, il ne s'en cachera pas, le Mathouriste a "vu" une parabole. Alors, cercles dans les deux directions, paraboles dans les deux directions, ou combiné paraboles dans la longueur, cercles dans la largeur? (ou paraboles-ellipses, si on considère les lignes matérialisées par la grille diagonale?)

Dans l'article cité plus haut, Beckh et Barthel ont testé diverse hypothèses, en confrontant des mesures in situ aux plans disponibles. Shukhov n'a laissé aucune indication précise sur la nature des courbes! Ils sont parvenus pour la grande arche à une allure parabolique, comme nous l'espérions, et proposent l'équation

y = 6.27 − 0.01706 x²

En prenant pour les deux réseaux de poutrelles portaant le toit, des arcs de parabole, on définirait un paraboloïde elliptique -dont on a mentionné plus haut qu'il est une surface de translation. Mais le plus simple ne serait-il pas que ces poutrelles soient des arcs de cercle, pour la simplicité de la fabrication? En ce cas, nous aurions "mal vu" le petit côté du rectangle, car l'arc le surmontant serait alors une portion d'ellipse. Mais cela n'en ferait que deux à fabriquer, contre tout le réseau si cet arc était circulaire... Nous vous suggérons de lire l'article et de faire votre conviction.

Quoiqu'il en soit, pour l'ingénieur, le système est efficace:

définir une surface de translation permet de fabriquer en grande série des éléments tous standards, facilement assemblables;
le réseau "croisé" permet de gagner 40% de métal à solidité égale.

Les Héritiers de Shukhov

L'article Rethinking Complexity: Vladimir Shukhov's steel lattice structures (références complètes ci-dessous) compare les principes architecturaux de ce toit avec celui réalisé au British Museum (Happold, Chris Williams): ce dernier doit raccorder un cylindre central au carré de bâtiments qui l'entoure.

Une première proposition a servi de base à une étude des déformations possibles afin d'ioptimiser la structure. L'influence de la méthode des éléments finis est ici évidente (née avec la montée en puissance des ordinateurs, elle décompose une surface en éléments de forme simple, souvent triangulaires, mais de taille variable, afin d'évaluer les forces sur chaque panneau; elle s'applique aussi bien à laoûte d'un barrage qu'au fuselage d'un avion ou la coque d'un navire). Mais de ce travail ont résulté 3312 panneaux de double vitrage, tous différents; et même si l'ordinateur délivre le mode d'assemblage de ce puzzle géant, les raccords aux 1826 points nodaux s'est révélé délicat...

Alors, comment ne pas être frappé par la simplicité des idées de Shukhov, exploitant la propriété de définition des surfaces de translation pour construire sa couverture à l'aide d'un grand nombre d'éléments standardisés, interchangeables et fabricables à la chaîne?

Joli sujet de dissertation sur l'intelligence géométrique de l'homme et les ressources offertes par les merveilleuses "bêtes à calcul" qu'il a su créer... le Mathouriste vous laisse méditer la question!

Comment visiter Londres sans aller voir les trésors du British Museum? Ce jour là, le Mathouriste pensait bien laisser ses maths au vestiaire et redevenir un touriste ordinaire... mais comment ne pas être frappé par ce plafond en éléments finis? Chassez les maths, elles reviennent au galop!

... Avant un Retour en Bohême!

Photo d'origine: G. Krämer

On passera d'abord par l'Allemagne: le journal Main Post relate, dans son édition du 15/12/2015, les travaux de restauration du Musée Franconien de Bad Wisheim avec un cliché très intéressant quant au procédé de contruction traditionnel en briques: sur les deux arcs (de cercle? d'ellipse? -il n'y aurait guère de différence perceptible à ce rayon et cet empattement) reposent des arcs parallèles -les lignes de briques- orientées à l'oblique (45°) par rapport au rectangle projetant la voûte: c'est, avant lui, le principe appliqué par Shukhov! Compte-tenu d'une taille plus modeste, mais en contrepartie d'un matériau plus fragile, la raison en est sans doute la même: renforcer la solidité; et l'on pariera volontiers sur l'empirisme d'artisans observateurs et expérimentés que sur de savants calculs.

On observera qu'il n'y a ici pas une, mais quatre surfaces de translation qui se rejoignent deux à deux selon des lignes parallèles aux arcs bordants, nettement marquées puisque les plans tangents à chacune des surfaces sont différents. L'état inachevé est une aubaine pour valider l'angle de 45° (ce n'est pas celui estimé optimal par Shukhov!) : le trou se projette suivant un carré.

Les images ci-dessous, empruntées au site d'une brasserie à Mariakirchen (Basse Bavière), montrent le résultat fini.


Photos recadrées sur la voûte (source: catalogue d'images de l'établissement)

Voilà qui commence à prouver que cette technique de construction a essaimé dans une partie de l'Europe Centrale. Mais, direz vous, si la Bavière nous rapproche... ce n'est tout de même pas la Bohême! Aussi le Mathouriste est-il retourné à ses stocks de souvenirs photographiques... et il y a trouvé l'église Sainte-Marie de l'Annonciation, à Litomerice (République Tchèque, pour donner la localisation actuelle; mais la région est dénommée Bohême du Nord.)

Adossée au Collège des Jésuites, elle a été construite entre 1701 et 1731 par l'architecte Octavio Broggio (1670-1742), qui a conçu plusieurs bâtiments religieux dans la région. Prenez donc le temps, en entrant, d'être saisi par la majesté du lieu... avant que la Géométrie ne reprenne ses droits!

Et maintenant, levons les yeux: cela, tout le monde le fait dans les églises. L'époque baroque a vu les plafonds rehaussés de peintures allégoriques, incluant souvent de savants trompe-l'œil, qui ne sauraient laisser le géomètre indifférent. Mais ce que nous voulons voir ici avant tout, ce sont les dômes de Bohème qui la constituent.
D'abord dans la nef, pour la partie à la décoration céleste (au fond, vers l'autel, la voûte à dominante blanche n'est plus qu'un berceau cylindrique.) Dans le sens de la nef, la voûte s'organise en arcs de cercles parallèles aux arches principales; dans le sens perpendiculaire, la forme translatée ne peut guère être le demi-cercle des arches bordant la nef, car le sommet se situerait plus haut; le plus probable est que l'on ait pris un arc de cercle tangent, de rayon un peu plus grand, et achevé les pendatifs "à main levée". Ne disposant ni de relevés de mesures, ni de plans, il est difficile d'être catégorique sur ce point, voire même d'être sûr qu'il s'agit de cercles... mais pensons aux ouvriers qui ont réalisé, avec un indéniable talent, cet ouvrage: comment obtenir une telle régularité sans employer un gabarit de construction? Le principe de simplicité veut que celui-ci soit circulaire (en outre, les fins connaisseurs de géométrie, dont le savoir dépassait droite et cercle, n'étaient pas légion en ce temps là)


		À regarder tout particulièrement! Aggrandissez en cliquant!!!

L'image qui mérite le plus d'attention est celle de droite: au niveau de la galerie latérale supérieure, le plafond reprend une autre voûte bohémienne, toujours sur une base rectangulaire; mais son "grand côté" est le "petit côté" de la nef. La vision des deux, côte à côte, souligne particulièrement bien l'effet produit par les surfaces de translation!

Voilà cette fois de quoi justifier pleinement l'énigmatique et fameuse dénomination: voûte bohémienne.
Il y a gros à parier que de nombreux autres exemples sont à découvrir dans cette belle région... les pas du Mathouriste ne l'ont pas encore mené à Brno, quoique cette ville figure en bonne place dans sa liste d'envies. Si vous y passez avant lui, n'hésitez pas à lui faire part de vos suggestions!

Et puis, bien sûr, quand on évoque la Bohême et le baroque... comment ne pas penser à Prague?


L'église Saint Nicolas de Staré Město est située sur la grand place, où trône la statue de Jan Hus. (Attention, il y a une autre église Saint Nicolas de l'autre côté de la Vltava, dans le quartier de Mala Strana); elle a été conçue entre 1732 et 1737 par l'architecte Kilian Ignace Dientzenhofer.(1689-1751), donc, un peu après celle de Litomerice... La voûte bohémienne y rend saisissante, par sa double courbure, l'impression prosuite par la peinture en trompe-l'œil d'un dôme à caissons, visiblement inspiré du Panthéon de Rome. Une autre encore domine l'orgue aux 2500 tuyaux!